Coordination Numbers
September 3, 2009 Posted by Emre S. Tasci
Recently, we are working on liquid alloys and for our work, we need the coordination number distribution. It’s kind of a gray area when you talk about coordination number of atoms in a liquid but it’s better than nothing to understand the properties and even more. I’d like to write a log on the tools I’ve recently coded/used in order to refer to in the future if a similar situation occurs. Also, maybe there are some others conducting similar research so, the tools introduced here may be helpful to them.
Recently, while searching recent publications on liquid alloys, I’ve found a very good and resourceful article on liquid Na-K alloys by Dr. J.-F. Wax (“Molecular dynamics study of the static structure of liquid Na-K alloys”, Physica B 403 (2008) 4241-48 | doi:10.1016/j.physb.2008.09.014). In this paper, among other properties, he had also presented the partial pair distribution functions. Partial-pair distribution functions is the averaged probability that you’ll encounter an atom in r distance starting from another atom. In solid phase, due to the symmetry of the crystal structure, you have discrete values instead of a continuous distribution and everything is crystal clear but I guess that’s the price we pay dealing with liquids. 8)
Partial-pair distribution functions are very useful in the sense that they let you derive the bond-length between constituent atom species, corresponding to the first minimums of the plots. Hence, one can see the neighborhood ranges by just looking at the plots.
I’ve sent a mail to Dr. Wax explaining my research topics and my interest and asking for his research data to which he very kindly and generously replied by providing his data.
He had sent me a big file with numerous configurations (coordinates of the atoms) following each other. The first -and the simplest- task was to split the file into seperate configuration files via this bash script:
#!/bin/bash
# Script Name: split_POS4.sh
# Splits the NaK conf files compilation POS4_DAT into sepearate
# conf files.
# Emre S. Tasci <e.tasci@tudelft.nl>
# 01/09/09
linestart=2
p="p"
for (( i = 1; i <= 1000; i++ ))
do
echo $i;
lineend=$(expr $linestart + 2047)
confname=$(printf "%04d" $i)
echo -e "3\n2048" > $confname
sed -n "$linestart,$(echo $lineend$p)" POS4_DAT >> $confname
linestart=$(expr $lineend + 1)
cat $confname | qhull i TO $confname.hull
done
(The compilation was of 1000 configurations, each with 2048 atoms)
As you can check in the line before the “done” closer, I’ve -proudly- used Qhull software to calculate the convex hull of each configuration. A convex hull is the -hopefully minimum- shape that covers all your system. So, for each configuration I now had 2 files: “xxxx” (where xxxx is the id/number of the configuration set) storing the coordinates (preceded by 3 and 2048, corresponding to dimension and number of atoms information for the qhull to parse & process) and “xxxx.hull” file, generated by the qhull, containing the vertices list of each facet (preceded by the total number of facets).
A facet is (in 3D) the plane formed by the vertice points. Imagine a cube, where an atom lies at each corner, 3 in the inside. So, we can say that our system consists of 11 atoms and the minimal shape that has edges selected from system’s atoms and covering the whole is a cube, with the edges being the 8 atoms at the corners. Now, add an atom floating over the face at the top. Now the convex hull that wraps our new system would no longer be a 6-faced, 8-edged cube but a 9-faced, 9-edged polygon. I need to know the convex hull geometry in order to correctly calculate the coordination number distributions (details will follow shortly).
The aforementioned two files look like:
sururi@husniya hull_calcs $ head 0001
3
2048
0.95278770E+00 0.13334565E+02 0.13376155E+02
0.13025256E+02 0.87618381E+00 0.20168993E+01
0.12745038E+01 0.14068998E-01 0.22887323E+01
0.13066590E+02 0.20788591E+01 0.58119183E+01
0.10468218E+00 0.58523640E-01 0.64288678E+01
0.12839412E+02 0.13117012E+02 0.79093881E+01
0.11918105E+01 0.12163854E+02 0.10270868E+02
0.12673985E+02 0.11642538E+02 0.10514597E+02
sururi@husniya hull_calcs $ head 0001.hull
180
568 1127 1776
1992 104 1551
956 449 1026
632 391 1026
391 632 1543
391 956 1026
966 632 1026
966 15 1039
632 966 1039The sets of 3 numbers in the xxxx.hull file is the ids/numbers of the atoms forming the edges of the facets, i.e., they are the vertices.
To calculate the coordination number distribution, you need to pick each atom and then simply count the other atoms within the cut-off distance depending on your atom’s and the neighboring atom’s species. After you do the counting for every atom, you average the results and voilà ! there is your CN distribution. But here’s the catch: In order to be able to count properly, you must make sure that, your reference atom’s cutoff radii stay within your system — otherwise you’ll be undercounting. Suppose your reference atom is one of the atoms at the corners of the cube: It will (generally/approximately) lack 7/8 of the neighbouring atoms it would normally have if it was to be the center atom of the specimen/sample. Remember that we are studying a continuous liquid and trying to model the system via ensembles of samples. So we should omit these atoms which has neighborhoods outside of our systems. Since neighborhoods are defined through bond-length, we should only include the atoms with a distance to the outside of at least cut-off radii. The “outside” is defined as the region outside the convex hull and it’s designated by the facets (planes).
From the xxxx.hull file, we have the ids of the vertice atoms and their coordinates are stored in the xxxx file. To define the plane equation
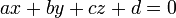
we will use the three vertice points, say p1, p2 and p3. From these 3 points, we calculate the normal n as:
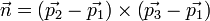
then, the plane equation (hence the coefficients a,b,c,d) can be derived by comparing the following equation:
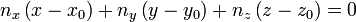
Here, (x0,y0,z0) are just the coordinates of any of the vertice points. And finally, the distance D between a point p1(x1,y1,z1) and a plane (a,b,c,d) is given by:
![D=\frac{\left|ax_{1}+by_{1}+cz_{1} \right|}{\sqrt[]{a^{2}+b^{2}+c^{2}}}](../tex/math/9167c920917483b1fb1d527814e55087.png)
Since vector operations are involved, I thought it’s better to do this job in Octave and wrote the following script that calculates the coefficients of the facets and then sets down to find out the points whose distances to all the facets are greater than the given cut-off radius:
sururi@husniya trunk $ cat octave_find_atoms_within.m
DummyA = 3;
%conf_index=292;
% Call from the command line like :
% octave -q --eval "Rcut=1.65;conf_index=293;path='$(pwd)';" octave_find_atoms_within.m
% hence specifying the conf_index at the command line.
% Emre S. Tasci <e.tasci@tudelft.nl> *
%
% From the positions and vertices file, calculates the plane
% equations (stored in "facet_coefficients") and then
% filters the atoms with respect to their distances to these
% facets. Writes the output to
% "hull_calcs/xxxx_insiders.txt" file
% 03/09/09 */
conf_index_name = num2str(sprintf("%04d",conf_index));;
%clock
clear facet_coefficients;
facet_coefficients = [];
global p v facet_coefficients
fp = fopen(strcat(path,"/hull_calcs/",conf_index_name));
k = fscanf(fp,"%d",2); % 1st is dim (=3), 2nd is number of atoms (=2048)
p = fscanf(fp,"%f",[k(1),k(2)]);
p = p';
fclose(fp);
%p = load("/tmp/del/delco");
fp = fopen(strcat(path,"/hull_calcs/",conf_index_name,".hull"));
k = fscanf(fp,"%d",1);% number of facets
v = fscanf(fp,"%d",[3,k]);
v = v';
fclose(fp);
%v = load("/tmp/del/delver");
function [a,b,c,d,e] = getPlaneCoefficients(facet_index)
global p v
% Get the 3 vertices
p1 = p(v(facet_index,1)+1,:); % The +1s come from the fact
p2 = p(v(facet_index,2)+1,:); % that qhull enumeration begins
p3 = p(v(facet_index,3)+1,:); % from 0 while Octave's from 1
%printf("%d: %f %f %f %f %f %f %f %f %f\n",facet_index,p1,p2,p3);
% Calculate the normal
n = cross((p2-p1),(p3-p1));
% Calculate the coefficients of the plane :
% ax + by + cz +d = 0
a = n(1);
b = n(2);
c = n(3);
d = -(dot(n,p1));
e = norm(n);
if(e==0)
printf("%f\n",p1);
printf("%f\n",p2);
printf("%f\n",p3);
printf("%d\n",facet_index);
endif
endfunction
function dist = distanceToPlane(point_index,facet_index)
global p facet_coefficients
k = facet_coefficients(facet_index,:);
n = [k(1) k(2) k(3)];
dist = abs(dot(n,p(point_index,:)) + k(4)) / k(5);
endfunction
for i = [1:size(v)(1)]
[a,b,c,d,e] = getPlaneCoefficients(i);
facet_coefficients = [ facet_coefficients ; [a,b,c,d,e]];
endfor
%Rcut = 1.65; % Defined from command line calling
% Find the points that are not closer than Rcut
inside_atoms = [];
for point = [1:size(p)(1)]
%for point = [1:100]
inside=true;
for facet = [1:size(v)(1)]
%for facet = [1:10]
%printf("%d - %d : %f\n",point,facet,dist);
if (distanceToPlane(point,facet)<Rcut)
inside = false;
break;
endif
endfor
if(inside)
inside_atoms = [inside_atoms point-1];
endif
endfor
fp = fopen(strcat(path,"/hull_calcs/",conf_index_name,"_insiders.txt"),"w");
fprintf(fp,"%d\n",inside_atoms);
fclose(fp);
%clock
This script is runned within the following php code which then takes the filtered atoms and does the counting using them:
<?PHP
/* Emre S. Tasci <e.tasci@tudelft.nl> *
*
* parse_configuration_data.php
*
* Written in order to parse the configuation files
* obtained from J.F. Wax in order to calculate the
* Coordination Number distribution. Each configuration
* file contain 2048 atoms' coordinates starting at the
* 3rd line. There is also a convex hull file generated
* using qhull (http://www.qhull.com) that contains the
* indexes (starting from 0) of the atoms that form the
* vertices of the convex hull. Finally there is the
* IP.dat file that identifies each atom (-1 for K; 1 for
* Na -- the second column is the relative masses).
*
* 02/09/09 */
/*
# if present, remove the previous run's results file
if(file_exists("results.txt"))
unlink("results.txt");
*/
error_reporting(E_ALL ^ E_NOTICE);
if(!file_exists("results.txt"))
{
$fp = fopen("results.txt","w");
fwrite($fp,"CONF#"."\tNa".implode("\tNa",range(1,20))."\tK".implode("\tK",range(1,20))."\n");
fclose($fp);
}
# Support for command line variable passing:
for($i=1;$i<sizeof($_SERVER["argv"]);$i++)
{
list($var0,$val0) = explode("=",$_SERVER["argv"][$i]);
$_GET[$var0] = $val0;
}
if($_GET["configuration"])
calculate($_GET["configuration"]);
else
exit("Please specify a configuration number [php parse_configuration_data.php configuration=xxx]\n");
function calculate($conf_index)
{
# Define the atoms array
$arr_atoms = Array();
# Get the information from the files
parse_types($arr_atoms);
$refs = get_vertices($conf_index);
parse_coordinates($arr_atoms,$conf_index);
# Define the Rcut-off values (obtained from partial parid distribution minimums)
$Rcut_arr = Array();
$Rscale = 3.828; # To convert reduced distances to Angstrom (if needed)
$Rscale = 1; # To convert reduced distances to Angstrom
$Rcut_arr["Na"]["Na"] = 1.38 * $Rscale;
$Rcut_arr["Na"]["K"] = 1.65 * $Rscale;
$Rcut_arr["K"]["Na"] = 1.65 * $Rscale;
$Rcut_arr["K"]["K"] = 1.52 * $Rscale;
$Rcut = $Rcut_arr["Na"]["K"]; # Taking the maximum one as the Rcut for safety
/*
# We have everything we need, so proceed to check
# if an atom is at safe distance wrt to the vertices
# Define all the ids
$arr_test_ids = range(0,2047);
# Subtract the ref atoms' ids
$arr_test_ids = array_diff($arr_test_ids, $refs);
sort($arr_test_ids);
//print_r($arr_test_ids);
$arr_passed_atom_ids = Array();
# Check each atom against refs
for($id=0, $size=sizeof($arr_test_ids); $id<$size; $id++)
{
//echo $id."\n";
$arr_atoms[$arr_test_ids[$id]]["in"] = TRUE;
foreach ($refs as $ref)
{
$distance = distance($arr_atoms[$arr_test_ids[$id]],$arr_atoms[$ref]);
//echo "\t".$ref."\t".$distance."\n";
if($distance < $Rcut)
{
$arr_atoms[$arr_test_ids[$id]]["in"] = FALSE;
break;
}
}
if($arr_atoms[$arr_test_ids[$id]]["in"] == TRUE)
$arr_passed_atom_ids[] = $arr_test_ids[$id];
}
*/
# Run the octave script file to calculate the inside atoms
if(!file_exists("hull_calcs/".sprintf("%04d",$conf_index)."_insiders.txt"))
exec("octave -q --eval \"Rcut=".$Rcut.";conf_index=".$conf_index.";path='$(pwd)';\" octave_find_atoms_within.m");
# Read the file generated by Octave
$arr_passed_atom_ids = file("hull_calcs/".sprintf("%04d",$conf_index)."_insiders.txt",FILE_IGNORE_NEW_LINES);
$arr_test_ids = range(0,2047);
$arr_test_ids = array_diff($arr_test_ids, $refs);
sort($arr_test_ids);
for($i=0, $size=sizeof($arr_test_ids);$i<$size;$i++)
$arr_atoms[$arr_test_ids[$i]]["in"]=FALSE;
# Begin checking every passed atom
foreach($arr_passed_atom_ids as $passed_atom_id)
{
$arr_atoms[$passed_atom_id]["in"] = TRUE;
for($i=0, $size=sizeof($arr_atoms); $i<$size; $i++)
{
$distance = distance($arr_atoms[$passed_atom_id],$arr_atoms[$i]);
//echo $passed_atom_id."\t---\t".$i."\n";
if($distance < $Rcut_arr[$arr_atoms[$passed_atom_id]["id"]][$arr_atoms[$i]["id"]] && $distance>0.001)
$arr_atoms[$passed_atom_id]["neighbour_count"] += 1;
}
}
# Do the binning
$CN_Na = Array();
$CN_K = Array();
for($i=0, $size=sizeof($arr_atoms); $i<$size; $i++)
{
if(array_key_exists("neighbour_count",$arr_atoms[$i]))
{
${"CN_".$arr_atoms[$i]['id']}[$arr_atoms[$i]["neighbour_count"]] += 1;
}
}
ksort($CN_Na);
ksort($CN_K);
//print_r($arr_atoms);
//print_r($CN_Na);
//print_r($CN_K);
# Report the results
$filename = "results/".sprintf("%04d",$conf_index)."_results.txt";
$fp = fopen($filename,"w");
fwrite($fp, "### Atoms array ###\n");
fwrite($fp,var_export($arr_atoms,TRUE)."\n");
fwrite($fp, "\n### CN Distribution for Na ###\n");
fwrite($fp,var_export($CN_Na,TRUE)."\n");
fwrite($fp, "\n### CN Distribution for K ###\n");
fwrite($fp,var_export($CN_K,TRUE)."\n");
# Percentage calculation:
$sum_Na = array_sum($CN_Na);
$sum_K = array_sum($CN_K);
foreach($CN_Na as $key=>$value)
$CN_Na[$key] = $value * 100 / $sum_Na;
foreach($CN_K as $key=>$value)
$CN_K[$key] = $value * 100 / $sum_K;
//print_r($CN_Na);
//print_r($CN_K);
fwrite($fp, "\n### CN Distribution (Percentage) for Na ###\n");
fwrite($fp,var_export($CN_Na,TRUE)."\n");
fwrite($fp, "\n### CN Distribution (Percentage) for K ###\n");
fwrite($fp,var_export($CN_K,TRUE)."\n");
fclose($fp);
# Write the summary to the results file
$fp = fopen("results.txt","a");
for($i=1;$i<=20;$i++)
{
if(!array_key_exists($i,$CN_Na))
$CN_Na[$i] = 0;
if(!array_key_exists($i,$CN_K))
$CN_K[$i] = 0;
}
ksort($CN_Na);
ksort($CN_K);
fwrite($fp,sprintf("%04d",$conf_index)."\t".implode("\t",$CN_Na)."\t".implode("\t",$CN_K)."\n");
fclose($fp);
}
function parse_types(&$arr_atoms)
{
# Parse the types
$i = 0;
$fp = fopen("IP.DAT", "r");
while(!feof($fp))
{
$line = fgets($fp,4096);
$auxarr = explode(" ",$line);
if($auxarr[0]==-1)
$arr_atoms[$i]["id"] = "Na";
else
$arr_atoms[$i]["id"] = "K";
$i++;
}
fclose($fp);
array_pop($arr_atoms);
return 0;
}
function get_vertices($conf_index)
{
$arr_refs = Array();
# Get the ids of the vertices of the convex hull
$filename = "hull_calcs/".sprintf("%04d",$conf_index).".hull";
$fp = fopen($filename, "r");
# Bypass the first line
$line = fgets($fp,4096);
while(!feof($fp))
{
$line = fgets($fp,4096);
$auxarr = explode(" ",$line);
array_pop($auxarr);
$arr_refs = array_merge($arr_refs, $auxarr);
}
fclose($fp);
// $arr_refs = array_unique($arr_refs); # This doesn't lose the keys
$arr_refs = array_keys(array_count_values($arr_refs)); # But this does.
return $arr_refs;
}
function parse_coordinates(&$arr_atoms, $conf_index)
{
# Parse the coordinates
$i = 0;
$filename = "hull_calcs/".sprintf("%04d",$conf_index);
$fp = fopen($filename, "r");
# Bypass the first two lines
$line = fgets($fp,4096);
$line = fgets($fp,4096);
while(!feof($fp))
{
$line = fgets($fp,4096);
$arr_atoms[$i]["coords"] = explode(" ",$line);
array_shift($arr_atoms[$i]["coords"]);
$i++;
}
fclose($fp);
array_pop($arr_atoms);
return 0;
}
function distance(&$atom1,&$atom2)
{
# Calculate the distance between the two atoms
$x1 = $atom1["coords"][0];
$x2 = $atom2["coords"][0];
$y1 = $atom1["coords"][1];
$y2 = $atom2["coords"][1];
$z1 = $atom1["coords"][2];
$z2 = $atom2["coords"][2];
return sqrt(pow($x1-$x2,2) + pow($y1-$y2,2) + pow($z1-$z2,2));
}
?>
The code above generates a “results/xxxx_results.txt” file containing all the information obtained in arrays format and also appends to “results.txt” file the relevant configuration file’s CN distribution summary. The systems can be visualized using the output generated by the following plotter.php script:
<?PHP
/* Emre S. Tasci <e.tasci@tudelft.nl> *
* Parses the results/xxxx_results.txt file and generates
* an XYZ file such that the atoms are labeled as the
* vertice atoms, close-vertice atoms and inside atoms..
* 02/09/09 */
# Support for command line variable passing:
for($i=1;$i<sizeof($_SERVER["argv"]);$i++)
{
list($var0,$val0) = explode("=",$_SERVER["argv"][$i]);
$_GET[$var0] = $val0;
}
if($_GET["configuration"])
$conf_index = $_GET["configuration"];
else
exit("Please specify a configuration number [php plotter.php configuration=xxx]\n");
$filename = sprintf("%04d",$conf_index);
# Get the atom array from the results file. Since results file
# contains other arrays as well, we slice the file using sed for the
# relevant part
$last_arr_line = exec('grep "### CN Distribution" results/'.$filename.'_results.txt -n -m1|sed "s:^\([0-9]\+\).*:\1:gi"');
exec('sed -n "2,'.($last_arr_line-1).'p" results/'.$filename.'_results.txt > system_tmp_array_dump_file');
$str=file_get_contents('system_tmp_array_dump_file');
$atom_arr=eval('return '.$str.';');
unlink('system_tmp_array_dump_file');
# Now that we have the coordinates, we itarate over the atoms to check
# the characteristic and designate them in the XYZ file.
$fp = fopen("system_".$filename.".xyz","w");
fwrite($fp,sizeof($atom_arr)."\n");
fwrite($fp,"Generated by plotter.php\n");
for($i=0, $size=sizeof($atom_arr);$i<$size;$i++)
{
if(!array_key_exists("in",$atom_arr[$i]))
$atomlabel = "Mg";#Vertices
elseif($atom_arr[$i]["in"]==TRUE)
$atomlabel = $atom_arr[$i]["id"];#Inside atoms
else
$atomlabel = "O";#Close-vertice atoms
fwrite($fp,$atomlabel."\t".implode("\t",$atom_arr[$i]["coords"]));
}
fclose($fp);
?>
which generates a “system_xxxx.xyz” file, ready to be viewed in a standard molecule viewing software. It designates the vertice atoms (of the convex hull, remember? 8)as “Mg” and the atoms close to them as “O” for easy-viewing purpose. A sample parsed file looks like this:
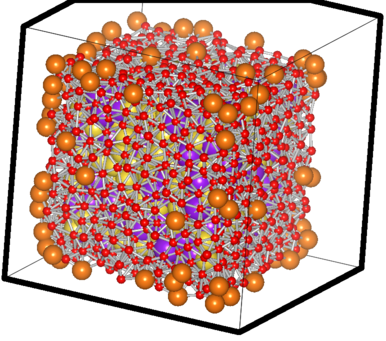
The filtered case of a sample Na-K system
The big orange atoms are the omitted vertice atoms; the small red ones are the atoms critically close to the facets and hence also omitted ones. You can see the purple and yellow atoms which have passed the test sitting happilly inside, with the counting done using them.. 8)
Binning is easy (with eyes closed – misunderstanding all you see..)
June 2, 2008 Posted by Emre S. Tasci
When you have some nice discrete random variables, or more correctly, some sets of nice discrete random variables and given that they behave well (like the ones you encounter all the time in the textbook examples), calculating the entropies and then moving on to the deducing of mutual information between these sets is never difficult. But things don’t happen that well in real situations: they tend to get nastier. The methods you employ for binary-valued sets are useless when you have 17000 different type of data among 25000 data points.
As an example, consider these two sets:
A={1,2,3,4,5}
B={1,121,43,12,100}
which one would you say is more ordered? A? Really? But how? — each of them has 5 different values which would amount to the same entropy for both. Yes, you can define two new sets based on these sets with actually having the differences between two adjacent members:
A’ = {1,1,1,1}
B’ = {120,-78,-31,88}
and the answer is obvious. This is really assuring – except the fact that it doesn’t have to be this obvious and furthermore, you don’t usually get only 6 membered sets to try out variations.
For this problem of mine, I have been devising a method and I think it’s working well. It’s really simple, you just bin (down) your data according some criteria and if it goes well, at the end you have classified your data points in much more smaller number of bins.
Today, I re-found the works of Dominik Endres and his colleagues. Their binning method is called the Bayesian Binning (you can find the detailed information at Endres’ personal page) and it pretty looks solid. I’ll still be focusing on my method (which I humbly call Tracking the Eskimo and the method itself compared to the Bayesian Binning, seems very primitive) but it’s always nice to see that, someone also had a similar problem and worked his way through it. There is also the other thing which I mention from time to time : when you treat your information as data, you get to have nice tools that were developed not by researchers from your field of interest but from totally different disciplines who were also at one time visited the 101010 world. 8) (It turns out that Dominik Endres and his fellows are from Psychology. One other thing is that I had begun thinking about my method after seeing another method for cytometry (the scientific branch which counts the cells in blood flow – or smt like that 8) applications…)
References:
D. Endres and P. Földiák, Bayesian bin distribution inference and mutual information, IEEE Transactions on Information Theory, vol. 51, no. 11, pp. 3766-3779, November 2005 DOI: 10.1109/TIT.2005.856954
D. Endres and P. Földiák, Exact Bayesian Bin Classification: a fast alternative to Bayesian Classification and its application to neural response analysis,
Journal of Computational Neuroscience, 24(1): 24-35, 2008. DOI: 10.1007/s10827-007-0039-5.
D. Endres, M. Oram, J. Schindelin and P. Földiák, Bayesian binning beats approximate alternatives: estimating peri-stimulus time histograms,
pp. 393-400, Advances in Neural Information Processing Systems 20, MIT Press, Cambridge, MA, 2008 http://books.nips.cc/nips20.html
Quote of the day: On Neural Networks and Bayesian Statistics
May 7, 2008 Posted by Emre S. Tasci
"The two ideas of neural network modelling and Bayesian statistics might seem uneasy bed-fellows. Neural networks are non-linear parallel computational devices inspired by the structure of the brain. ‘Backpropagation networks’ are able to learn, by example, to solve prediction and classification problems. Such a neural network is typically viewed as a black box which finds by hook or by crook an incomprehensible solution to a poorly understood problem. In contrast, Bayesian methods are characterized by an insistence on coherent inference based on clearly defined axioms; in Bayesian circles, and ‘ad hockery’ is a capital offense. Thus Bayesian statistics and neural networks might seem to occupy opposite extremes of the data modelling spectrum."
Probable Networks and Plausible Predictions – A Review of Practical Bayesian Methods for Supervised Neural Networks *
David J.C. MacKay *
Specification of an extensible and portable file format for electronic structure and crystallographic data
May 6, 2008 Posted by Emre S. Tasci
Specification of an extensible and portable file format for electronic structure and crystallographic data
X. Gonzea, C.-O. Almbladh, A. Cucca, D. Caliste, C. Freysoldt, M.A.L. Marques, V. Olevano, Y. Pouillon and M.J. Verstraet
Comput. Mater. Sci. (2008) doi:10.1016/j.commatsci.2008.02.023
Abstract
In order to allow different software applications, in constant evolution, to interact and exchange data, flexible file formats are needed. A file format specification for different types of content has been elaborated to allow communication of data for the software developed within the European Network of Excellence “NANOQUANTA”, focusing on first-principles calculations of materials and nanosystems. It might be used by other software as well, and is described here in detail. The format relies on the NetCDF binary input/output library, already used in many different scientific communities, that provides flexibility as well as portability across languages and platforms. Thanks to NetCDF, the content can be accessed by keywords, ensuring the file format is extensible and backward compatible.
Keywords
Electronic structure; File format standardization; Crystallographic datafiles; Density datafiles; Wavefunctions datafiles; NetCDF
PACS classification codes
61.68.+n; 63.20.dk; 71.15.Ap
Problems with the binary representations:
- lack of portability between big-endian and little-endian platforms (and vice-versa), or between 32-bit and 64-bit platforms;
- difficulties to read the files written by F77/90 codes from C/C++ software (and vice-versa)
- lack of extensibility, as one file produced for one version of the software might not be readable by a past/forthcoming version
(Network Common Data Form) library solves these issues. (Alas, it is binary and in the examples presented in http://www.unidata.ucar.edu/software/netcdf/examples/files.html, it seems like the CDF representations are larger in size than those of the CDL metadata representations)
The idea of standardization of file formats is not new in the electronic structure community [X. Gonze, G. Zerah, K.W. Jakobsen, and K. Hinsen. Psi-k Newsletter 55, February 2003, pp. 129-134. URL: <http://psi-k.dl.ac.uk>] (This article is a must read article, by the way. It’s a very insightful and concerning overview of the good natured developments in the atomistic/molecular software domain. It is purifying in the attempt to produce something good..). However, it proved difficult to achieve without a formal organization, gathering code developers involved in different software project, with a sufficient incentive to realize effective file exchange between such software.
HDF (Hierarchical Data Format) is also an alternative. NetCDF is simpler to use if the data formats are flat, while HDF has definite advantages if one is dealing with hierarchical formats. Typically, we will need to describe many different multi-dimensional arrays of real or complex numbers, for which NetCDF is an adequate tool.
Although a data specification might be presented irrespective of the library actually used for the implementation, such a freedom might lead to implementations using incompatible file formats (like NetCDF and XML for instance). This possibility would in effect block the expected standardization gain. Thus, as a part of the standardization, we require the future implementations of our specification to rely on the NetCDF library only. (Alternative to independent schemas is presented as a mandatory format which is against the whole idea of development. The reason for NetCDF being incompatible with XML lies solely on the inflexibility/inextensibility of the prior format. Although such a readily defined and built format is adventageous considering the huge numerical data and parameters the ab inito software uses, it is very immobile and unnecessary for compound and element data.)
The compact representation brought by NetCDF can be by-passed in favour of text encoding (very agreable given the usage purposes: XML type extensible schema usage is much more adequate for structure/composition properties). We are aware of several standardization efforts [J. Junquera, M. Verstraete, X. Gonze, unpublished] and [J. Mortensen, F. Jollet, unpublished. Also check Minutes of the discussion on XML format for PAW setups], relying on XML, which emphasize addressing by content to represent such atomic data.
4 types of data types are distinguished:
- (A) The actual numerical data (which defines whether a file contains wavefunctions, a density, etc), for which a name must have been agreed in the specification.
- (B) The auxiliary data that is mandatory to make proper usage of the actual numerical data of A-type. The name and description of this auxiliary information is also agreed.
- (C) The auxiliary data that is not mandatory to make proper usage of the A-type numerical data, but for which a name and description has been agreed in the specification.
- (D) Other data, typically code-dependent, whose availability might help the use of the file for a specific code. The name of these variables should be different from the names chosen for agreed variables of A–C types. Such type D data might even be redundant with type A–C data.
The NetCDF interface adapts the dimension ordering to the programming language used. The notation here is C-like, i.e. row-major storage, the last index varying the fastest. In FORTRAN, a similar memory mapping is obtained by reversing the order of the indices. (So, the ordering/reverse-ordering is handled by the interface/library)
Concluding Remarks
We presented the specifications for a file format relying on the NetCDF I/O library with a content related to electronic structure and crystallographic data. This specification takes advantage of all the interesting properties of NetCDF-based files, in particular portability and extensibility. It is designed for both serial and distributed usage, although the latter characteristics was not presented here.
Several software in the Nanoquanta and ETSF [15] context can produce or read this file format: ABINIT [16] and [17], DP [18], GWST, SELF [19], V_Sim [20]. In order to further encourage its use, a library of Fortran routines [5] has been set up, and is available under the GNU LGPL licence.
Additional Information:
Announcement for a past event
( http://www.tddft.org/pipermail/fsatom/2003-February/000004.html )
CECAM – psi-k – SIMU joint Tutorial
1) Title : Software solutions for data exchange and code gluing.
Location : Lyon Dates : 8-10 october, 2003
Purpose : In this tutorial, we will teach software tools and standards that have recently emerged in view of the exchange of data (text and binary) and gluing of codes : (1) Python, as scripting language, its interfaces with C and FORTRAN ; (2) XML, a standard for representing structured data in text files ; (3) netCDF, a library and file format for the exchange and storage of binary data, and its interfaces with C, Fortran, and Python
Organizers : X. Gonze gonze@pcpm.ucl.ac.be
K. Hinsen hinsen@cnrs-orleans.fr
2) Scientific content
Recent discussions, related to the CECAM workshop on "Open Source Software for Microscopic Simulations", June 19-21, 2002, to the GRID concept (http://www.gridcomputing.com), as well as to the future Integrated Infrastructure Initiative proposal linked to the European psi-k network (http://psi-k.dl.ac.uk), have made clear that one challenge for the coming years is the ability to establish standards for accessing codes, transferring data between codes, testing codes against each other, and become able to "glue" them (this being facilitated by the Free Software concept).
In the present tutorial, we would like to teach three "software solutions" to face this challenge : Python, XML and netCDF.
Python is now the de facto "scripting langage" standard in the computational physics and chemistry community. XML (eXtended Markup Language) is a framework for building mark-up languages, allowing to set-up self-describing documents, readable by humans and machines. netCDF allows binary files to be portable accross platforms. It is not our aim to cover all possible solutions to the above-mentioned challenges (e.g. PERL, Tcl, or HDF), but these three have proven suitable for atomic-scale simulations, in the framework of leading projects like CAMPOS (http://www.fysik.dtu.dk/campos), MMTK (http://dirac.cnrs-orleans.fr/MMTK), and GROMACS (http://www.gromacs.org). Other software projects like ABINIT (http://www.abinit.org) and PWSCF (http://www.pwscf.org – in the DEMOCRITOS context), among others, have made clear their interest for these. All of these software solutions can be used without having to buy a licence.
Tentative program of the tutorial. Lectures in the morning, hands-on training in the afternoon.
1st day ——- 2h Python basics 1h Interface : Python/C or FORTRAN 1h XML basics Afternoon Training with Python, and interfaces with C and FORTRAN
2nd day ——- 2h Python : object oriented (+ an application to GUI and Tk) 1h Interface : Python/XML 1h Interface : XML + C or FORTRAN Afternoon Training with XML + interfaces
3rd day ——- 1h Python : numerical 1h netCDF basics 1h Interface : netCDF/Python 1h Interface : netCDF/C or FORTRAN Afternoon Training with netCDF + interfaces
3) List of lecturers
K. Hinsen (Orleans, France), organizer X. Gonze (Louvain-la-Neuve, Belgium), organizer K. Jakobsen (Lyngby, Denmark), instructor J. Schiotz (Lyngby, Denmark), instructor J. Van Der Spoel (Groningen, The Netherlands), instructor M. van Loewis (Berlin, Germany), instructor
4) Number of participants : around 20, Most of the participants should be PhD students, postdoc or young permanent scientists, involved in code development. It is assumed that the attendants have a good knowledge of UNIX, and C or FORTRAN.
Our budget will allow contributing to travel and local expenses of up to 20 participants.
XML and NetCDF:
from Specification of file formats for NANOQUANTA/ETSF Specification – www.etsf.eu/research/software/nq_specff_v2.1_final.pdf
Section 1. General considerations concerning the present file format specifications.
One has to consider separately the set of data to be included in each of different types of files, from their representation. Concerning the latter, one encounters simple text files, binary files, XML-structured files, NetCDF files, etc … It was already decided previously (Nanoquanta meeting Maratea Sept. 2004) to evolve towards formats that deal appropriately with the self- description issue, i.e. XML and NetCDF. The inherent flexibility of these representations will also allow to evolve specific versions of each type of files progressively, and refine earlier working proposals. The same direction has been adopted by several groups of code developers that we know of.
Information on NetCDF and XML can be obtained from the official Web sites,
http://www.unidata.ucar.edu/software/netcdf/ and
http://www.w3.org/XML/
There are numerous other presentations of these formats on the Web, or in books.
The elaboration of file formats based on NetCDF has advanced a lot during the Louvain-la- Neuve mini-workshop. There has been also some remarks about XML.
Concerning XML :
(A) The XML format is most adapted for the structured representation of relatively small quantity of data, as it is not compressed.
(B) It is a very flexible format, but hard to read in Fortran (no problem in C, C++ or Python). Recently, Alberto Garcia has set up a XMLF90 library of routines to read XML from Fortran. http://lcdx00.wm.lc.ehu.es/~wdpgaara/xml/index.html Other efforts exists in this direction http://nn-online.org/code/xml/
Concerning NetCDF
- (A) Several groups of developers inside NQ have already a good experience of using it, for the representation of binary data (large files).
- (B) Although there is no clear advantage of NetCDF compared to HDF (another possibility for large binary files), this experience inside the NQ network is the main reason for preferring it. By the way, NetCDF and HDF are willing to merge (this might take a few years, though).
- (C) File size limitations of NetCDF exist, see appendix D, but should be overcome in the future.
Thanks to the flexibility of NetCDF, the content of a NetCDF file format suitable for use for NQ softwares might be of four different types :
(1) The actual numerical data (that defines a file for wavefunctions, or a density file, etc …), whose NetCDF description would have been agreed.
(2) The auxiliary data that are mandatory to make proper usage of the actual numerical data. The NetCDF description of these auxiliary data should also be agreed.
(3) The auxiliary data that are not mandatory, but whose NetCDF description has been agreed, in a larger context.
(4) Other data, typically code-dependent, whose existence might help the use of the file for a specific code.
References:
[5] URL: <http://www.etsf.eu/index.php?page=tools>.
[15] URL: <http://www.etsf.eu/>.
[16] X. Gonze, J.-M. Beuken, R. Caracas, F. Detraux, M. Fuchs, G.-M. Rignanese, L. Sindic, M. Verstraete, G. Zerah, F. Jollet, M. Torrent, A. Roy, M. Mikami, Ph. Ghosez, J.-Y. Raty and D.C. Allan, Comput. Mater. Sci. 25 (2002), pp. 478–492.
[17] X. Gonze, G.-M. Rignanese, M. Verstraete, J.-M. Beuken, Y. Pouillon, R. Caracas, F. Jollet, M. Torrent, G. Zérah, M. Mikami, Ph. Ghosez, M. Veithen, J.-Y. Raty, V. Olevano, F. Bruneval, L. Reining, R. Godby, G. Onida, D.R. Hamann and D.C. Allan, Zeit. Kristall. 220 (2005), pp. 558–562.
[18] URL: <http://dp-code.org>.
[19] URL: <http://www.bethe-salpeter.org>.
[20] URL: http://www-drfmc.cea.fr/sp2m/L_Sim/V_Sim/index.en.html.
A (Lame) Proof of the Probability Sum Rule
December 21, 2007 Posted by Emre S. Tasci
Q: Prove the Probability Sum Rule, that is:
![Formula: % MathType!MTEF!2!1!+-<br />
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm<br />
% aabaGaamOqaaGaayjkaiaawMcaaiabg2da9maaqahabaGaamiuamaa<br />
% bmaabaGaamOqaiaacYhacaWGbbGaeyypa0JaamODamaaBaaaleaaca<br />
% WGQbaabeaaaOGaayjkaiaawMcaaiaadcfadaqadaqaaiaadgeacqGH<br />
% 9aqpcaWG2bWaaSbaaSqaaiaadQgaaeqaaaGccaGLOaGaayzkaaaale<br />
% aacaWGQbGaeyypa0JaaGymaaqaaiaadUgaa0GaeyyeIuoaaaa!4E55!<br />
\[<br />
P\left( B \right) = \sum\limits_{j = 1}^k {P\left( {B|A = v_j } \right)P\left( {A = v_j } \right)} <br />
\]<br />](../latex_cache/62e60b9fc34d0d25c3a8afd94d6e714a.png)
(where A is a random variable with arity (~dimension) k) using Axioms:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGimaiabgs
% MiJkaadcfadaqadaqaaiaadgeaaiaawIcacaGLPaaacqGHKjYOcaaI
% XaGaaiilaiaaykW7caWGqbWaaeWaaeaacaWGubGaamOCaiaadwhaca
% WGLbaacaGLOaGaayzkaaGaeyypa0JaaGymaiaacYcacaWGqbWaaeWa
% aeaacaWGgbGaamyyaiaadYgacaWGZbGaamyzaaGaayjkaiaawMcaai
% abg2da9iaaicdacaWLjaWaamWaaeaacaaIXaaacaGLBbGaayzxaaaa
% aa!549F!
\[
0 \leqslant P\left( A \right) \leqslant 1,\,P\left( {True} \right) = 1,P\left( {False} \right) = 0 & \left[ 1 \right]
\]](../latex_cache/ebad3f22470cede53f8dd5d8793faca8.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamyqaiabgIIiAlaadkeaaiaawIcacaGLPaaacqGH9aqpcaWG
% qbWaaeWaaeaacaWGbbaacaGLOaGaayzkaaGaey4kaSIaamiuamaabm
% aabaGaamOqaaGaayjkaiaawMcaaiabgkHiTiaadcfadaqadaqaaiaa
% dgeacqGHNis2caWGcbaacaGLOaGaayzkaaGaaCzcamaadmaabaGaaG
% OmaaGaay5waiaaw2faaaaa!4D8F!
\[
P\left( {A \vee B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \wedge B} \right) & \left[ 2 \right]
\]](../latex_cache/a72d4f7a438f69245af49a44040c4757.png)
and assuming:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiaacI
% cacaWGbbGaeyypa0JaamODamaaBaaaleaacaWGPbaabeaakiabgEIi
% zlaadgeacqGH9aqpcaWG2bWaaSbaaSqaaiaadQgaaeqaaOGaaiykai
% abg2da9maaceaabaqbaeqabiGaaaqaaiaaicdaaeaacaqGPbGaaeOz
% aiaabccacaWGPbGaeyiyIKRaamOAaaqaaiaadcfadaqadaqaaiaadg
% eacqGH9aqpcaWG2bWaaSbaaSqaaiaadMgaaeqaaaGccaGLOaGaayzk
% aaaabaGaaeyAaiaabAgacaqGGaGaamyAaiabg2da9iaadQgaaaGaaC
% zcamaadmaabaGaaG4maaGaay5waiaaw2faaaGaay5Eaaaaaa!599B!
\[
P(A = v_i \wedge A = v_j ) = \left\{ {\begin{array}{*{20}c}
0 & {{\text{if }}i \ne j} \\
{P\left( {A = v_i } \right)} & {{\text{if }}i = j} \\
\end{array} & \left[ 3 \right]} \right.
\]](../latex_cache/a314124eb481a56ec193e25f7cd587f4.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiaacI
% cacaWGbbGaeyypa0JaamODamaaBaaaleaacaaIXaaabeaakiabgIIi
% AlaadgeacqGH9aqpcaWG2bWaaSbaaSqaaiaaikdaaeqaaOGaeyikIO
% TaaiOlaiaac6cacaGGUaGaeyikIOTaamyqaiabg2da9iaadAhadaWg
% aaWcbaGaam4AaaqabaGccaGGPaGaeyypa0JaaGymaiaaxMaacaWLja
% WaamWaaeaacaaI0aaacaGLBbGaayzxaaaaaa!5054!
\[
P(A = v_1 \vee A = v_2 \vee ... \vee A = v_k ) = 1 & & \left[ 4 \right]
\]](../latex_cache/72a54737587e492b8e8a9cd08d9345ca.png)
We will first prove the following equalities to make use of them later in the actual proof:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamyqaiabg2da9iaadAhadaWgaaWcbaGaaGymaaqabaGccqGH
% OiI2caWGbbGaeyypa0JaamODamaaBaaaleaacaaIYaaabeaakiabgI
% IiAlaac6cacaGGUaGaaiOlaiabgIIiAlaadgeacqGH9aqpcaWG2bWa
% aSbaaSqaaiaadMgaaeqaaaGccaGLOaGaayzkaaGaeyypa0ZaaabCae
% aacaWGqbWaaeWaaeaacaWGbbGaeyypa0JaamODamaaBaaaleaacaWG
% QbaabeaaaOGaayjkaiaawMcaaiaaxMaadaWadaqaaiaaiwdaaiaawU
% facaGLDbaaaSqaaiaadQgacqGH9aqpcaaIXaaabaGaamyAaaqdcqGH
% ris5aaaa!5B50!
\[
P\left( {A = v_1 \vee A = v_2 \vee ... \vee A = v_i } \right) = \sum\limits_{j = 1}^i {P\left( {A = v_j } \right) & \left[ 5 \right]} \]](../latex_cache/d277219eacdba2da3118abce6c75cffe.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamOqaiabgEIizpaadmaabaGaamyqaiabg2da9iaadAhadaWg
% aaWcbaGaaGymaaqabaGccqGHOiI2caWGbbGaeyypa0JaamODamaaBa
% aaleaacaaIYaaabeaakiabgIIiAlaac6cacaGGUaGaaiOlaiabgIIi
% AlaadgeacqGH9aqpcaWG2bWaaSbaaSqaaiaadMgaaeqaaaGccaGLBb
% GaayzxaaaacaGLOaGaayzkaaGaeyypa0ZaaabCaeaacaWGqbWaaeWa
% aeaacaWGcbGaey4jIKTaamyqaiabg2da9iaadAhadaWgaaWcbaGaam
% OAaaqabaaakiaawIcacaGLPaaacaWLjaWaamWaaeaacaaI2aaacaGL
% BbGaayzxaaaaleaacaWGQbGaeyypa0JaaGymaaqaaiaadMgaa0Gaey
% yeIuoaaaa!622D!
\[
P\left( {B \wedge \left[ {A = v_1 \vee A = v_2 \vee ... \vee A = v_i } \right]} \right) = \sum\limits_{j = 1}^i {P\left( {B \wedge A = v_j } \right) & \left[ 6 \right]}
\]](../latex_cache/7058ad55f03fe94f5b053a640ebd6d6f.png)
Proof of [5]:
Using [2], we can write:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamyqaiabg2da9iaadAhadaWgaaWcbaGaamyAaaqabaGccqGH
% OiI2caWGbbGaeyypa0JaamODamaaBaaaleaacaWGQbaabeaaaOGaay
% jkaiaawMcaaiabg2da9iaadcfadaqadaqaaiaadgeacqGH9aqpcaWG
% 2bWaaSbaaSqaaiaadMgaaeqaaaGccaGLOaGaayzkaaGaey4kaSIaam
% iuamaabmaabaGaamyqaiabg2da9iaadAhadaWgaaWcbaGaamOAaaqa
% baaakiaawIcacaGLPaaacqGHsislcaWGqbWaaeWaaeaacaWGbbGaey
% ypa0JaamODamaaBaaaleaacaWGPbaabeaakiabgEIizlaadgeacqGH
% 9aqpcaWG2bWaaSbaaSqaaiaadQgaaeqaaaGccaGLOaGaayzkaaaaaa!5D1D!
\[
P\left( {A = v_i \vee A = v_j } \right) = P\left( {A = v_i } \right) + P\left( {A = v_j } \right) - P\left( {A = v_i \wedge A = v_j } \right)
\]](../latex_cache/8ad40fe5a36e479a716cecfee659bf7c.png)
where, from the assumption [3], we have
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamyqaiabg2da9iaadAhadaWgaaWcbaGaamyAaaqabaGccqGH
% OiI2caWGbbGaeyypa0JaamODamaaBaaaleaacaWGQbaabeaaaOGaay
% jkaiaawMcaaiabg2da9iaadcfadaqadaqaaiaadgeacqGH9aqpcaWG
% 2bWaaSbaaSqaaiaadMgaaeqaaaGccaGLOaGaayzkaaGaey4kaSIaam
% iuamaabmaabaGaamyqaiabg2da9iaadAhadaWgaaWcbaGaamOAaaqa
% baaakiaawIcacaGLPaaacaWLjaGaaCzcamaabmaabaGaamyAaiabgc
% Mi5kaadQgaaiaawIcacaGLPaaaaaa!56BE!
\[
P\left( {A = v_i \vee A = v_j } \right) = P\left( {A = v_i } \right) + P\left( {A = v_j } \right) & & \left( {i \ne j} \right)
\]](../latex_cache/f0f86924b7e7208973f0ec5eb717ea6d.png)
Using this fact, we can now expand the LHS of [5] as:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb
% WaaeWaaeaacaWGbbGaeyypa0JaamODamaaBaaaleaacaaIXaaabeaa
% kiabgIIiAlaadgeacqGH9aqpcaWG2bWaaSbaaSqaaiaaikdaaeqaaO
% GaeyikIOTaaiOlaiaac6cacaGGUaGaeyikIOTaamyqaiabg2da9iaa
% dAhadaWgaaWcbaGaamyAaaqabaaakiaawIcacaGLPaaacqGH9aqpca
% WGqbWaaeWaaeaacaWGbbGaeyypa0JaamODamaaBaaaleaacaaIXaaa
% beaaaOGaayjkaiaawMcaaiabgUcaRiaadcfadaqadaqaaiaadgeacq
% GH9aqpcaWG2bWaaSbaaSqaaiaaikdaaeqaaaGccaGLOaGaayzkaaGa
% ey4kaSIaaiOlaiaac6cacaGGUaGaey4kaSIaamiuamaabmaabaGaam
% yqaiabg2da9iaadAhadaWgaaWcbaGaamyAaaqabaaakiaawIcacaGL
% PaaaaeaacqGH9aqpdaaeWbqaaiaadcfadaqadaqaaiaadgeacqGH9a
% qpcaWG2bWaaSbaaSqaaiaadQgaaeqaaaGccaGLOaGaayzkaaaaleaa
% caWGQbGaeyypa0JaaGymaaqaaiaadMgaa0GaeyyeIuoaaaaa!703C!
\[
\begin{gathered}
P\left( {A = v_1 \vee A = v_2 \vee ... \vee A = v_i } \right) = P\left( {A = v_1 } \right) + P\left( {A = v_2 } \right) + ... + P\left( {A = v_i } \right) \hfill \\
= \sum\limits_{j = 1}^i {P\left( {A = v_j } \right)} \hfill \\
\end{gathered}
\]](../latex_cache/510884db138003e4c3aaab2ae86a1de8.png)
Proof of [6]:
Using the distribution property, we can write the LHS of [6] as:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb
% WaaeWaaeaacaWGcbGaey4jIK9aamWaaeaacaWGbbGaeyypa0JaamOD
% amaaBaaaleaacaaIXaaabeaakiabgIIiAlaadgeacqGH9aqpcaWG2b
% WaaSbaaSqaaiaaikdaaeqaaOGaeyikIOTaaiOlaiaac6cacaGGUaGa
% eyikIOTaamyqaiabg2da9iaadAhadaWgaaWcbaGaamyAaaqabaaaki
% aawUfacaGLDbaaaiaawIcacaGLPaaaaeaacqGH9aqpcaWGqbWaaeWa
% aeaadaWadaqaaiaadkeacqGHNis2caWGbbGaeyypa0JaamODamaaBa
% aaleaacaaIXaaabeaaaOGaay5waiaaw2faaiabgIIiApaadmaabaGa
% amOqaiabgEIizlaadgeacqGH9aqpcaWG2bWaaSbaaSqaaiaaikdaae
% qaaaGccaGLBbGaayzxaaGaeyikIOTaaiOlaiaac6cacaGGUaGaeyik
% IO9aamWaaeaacaWGcbGaey4jIKTaamyqaiabg2da9iaadAhadaWgaa
% WcbaGaamyAaaqabaaakiaawUfacaGLDbaaaiaawIcacaGLPaaaaaaa
% !7256!
\[
\begin{gathered}
P\left( {B \wedge \left[ {A = v_1 \vee A = v_2 \vee ... \vee A = v_i } \right]} \right) \hfill \\
= P\left( {\left[ {B \wedge A = v_1 } \right] \vee \left[ {B \wedge A = v_2 } \right] \vee ... \vee \left[ {B \wedge A = v_i } \right]} \right) \hfill \\
\end{gathered}
\]](../latex_cache/2f9335a3273caee21f73408b5860e8be.png)
from [2], it is obvious that:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb
% WaaeWaaeaadaWadaqaaiaadkeacqGHNis2caWGbbGaeyypa0JaamOD
% amaaBaaaleaacaWGPbaabeaaaOGaay5waiaaw2faaiabgIIiApaadm
% aabaGaamOqaiabgEIizlaadgeacqGH9aqpcaWG2bWaaSbaaSqaaiaa
% dQgaaeqaaaGccaGLBbGaayzxaaaacaGLOaGaayzkaaaabaGaeyypa0
% JaamiuaiaacIcacaWGcbGaey4jIKTaamyqaiabg2da9iaadAhadaWg
% aaWcbaGaamyAaaqabaGccaGGPaGaey4kaSIaamiuaiaacIcacaWGcb
% Gaey4jIKTaamyqaiabg2da9iaadAhadaWgaaWcbaGaamOAaaqabaGc
% caGGPaGaeyOeI0YaaGbaaeaacaWGqbWaaeWaaeaadaWadaqaaiaadk
% eacqGHNis2caWGbbGaeyypa0JaamODamaaBaaaleaacaWGPbaabeaa
% aOGaay5waiaaw2faaiabgEIizpaadmaabaGaamOqaiabgEIizlaadg
% eacqGH9aqpcaWG2bWaaSbaaSqaaiaadQgaaeqaaaGccaGLBbGaayzx
% aaaacaGLOaGaayzkaaaaleaacaaIWaGaaGPaVpaabmaabaGaamyAai
% abgcMi5kaadQgaaiaawIcacaGLPaaaaOGaayjo+daabaGaeyypa0Ja
% amiuaiaacIcacaWGcbGaey4jIKTaamyqaiabg2da9iaadAhadaWgaa
% WcbaGaamyAaaqabaGccaGGPaGaey4kaSIaamiuaiaacIcacaWGcbGa
% ey4jIKTaamyqaiabg2da9iaadAhadaWgaaWcbaGaamOAaaqabaGcca
% GGPaaaaaa!8FC2!
\[
\begin{gathered}
P\left( {\left[ {B \wedge A = v_i } \right] \vee \left[ {B \wedge A = v_j } \right]} \right) \hfill \\
= P(B \wedge A = v_i ) + P(B \wedge A = v_j ) - \underbrace {P\left( {\left[ {B \wedge A = v_i } \right] \wedge \left[ {B \wedge A = v_j } \right]} \right)}_{0\,\left( {i \ne j} \right)} \hfill \\
= P(B \wedge A = v_i ) + P(B \wedge A = v_j ) \hfill \\
\end{gathered}
\]](../latex_cache/c1836e72053a84a464bfc83b1c9de440.png)
then using [5], we can rearrange and rewrite the LHS of [6] as:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb
% WaaeWaaeaacaWGcbGaey4jIK9aamWaaeaacaWGbbGaeyypa0JaamOD
% amaaBaaaleaacaaIXaaabeaakiabgIIiAlaadgeacqGH9aqpcaWG2b
% WaaSbaaSqaaiaaikdaaeqaaOGaeyikIOTaaiOlaiaac6cacaGGUaGa
% eyikIOTaamyqaiabg2da9iaadAhadaWgaaWcbaGaamyAaaqabaaaki
% aawUfacaGLDbaaaiaawIcacaGLPaaaaeaacqGH9aqpcaWGqbGaaiik
% aiaadkeacqGHNis2caWGbbGaeyypa0JaamODamaaBaaaleaacaaIXa
% aabeaakiaacMcacqGHRaWkcaWGqbGaaiikaiaadkeacqGHNis2caWG
% bbGaeyypa0JaamODamaaBaaaleaacaaIYaaabeaakiaacMcacqGHRa
% WkcaGGUaGaaiOlaiaac6cacqGHRaWkcaWGqbGaaiikaiaadkeacqGH
% Nis2caWGbbGaeyypa0JaamODamaaBaaaleaacaWGPbaabeaakiaacM
% caaeaacqGH9aqpdaaeWbqaaiaadcfadaqadaqaaiaadkeacqGHNis2
% caWGbbGaeyypa0JaamODamaaBaaaleaacaWGQbaabeaaaOGaayjkai
% aawMcaaaWcbaGaamOAaiabg2da9iaaigdaaeaacaWGPbaaniabggHi
% Ldaaaaa!7DE8!
\[
\begin{gathered}
P\left( {B \wedge \left[ {A = v_1 \vee A = v_2 \vee ... \vee A = v_i } \right]} \right) \hfill \\
= P(B \wedge A = v_1 ) + P(B \wedge A = v_2 ) + ... + P(B \wedge A = v_i ) \hfill \\
= \sum\limits_{j = 1}^i {P\left( {B \wedge A = v_j } \right)} \hfill \\
\end{gathered}
\]](../latex_cache/65fa4f33cf4d68a921284ef752dc381c.png)
Final Proof :
Before proceeding, I will include two assumptions about the Universal Set (this part is the main reason for the proof to be lame by the way).
Define the universal set U as the set that includes all possible values of some random variable X. All the other sets are subsets of U and for an arbitrary set A, we assume that:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGbb
% Gaey4jIKTaamyvaiabg2da9iaadgeaaeaacaWGbbGaeyikIOTaamyv
% aiabg2da9iaadwfaaaaa!403E!
\[
\begin{gathered}
A \wedge U = A \hfill \\
A \vee U = U \hfill \\
\end{gathered}
\]](../latex_cache/400e2fd05e05d98164d3a0849bb8c851.png)
Furthermore, we will be assuming that, a condition that includes all the possible outcomes(/values) for a variable A is equivalent to the universal set. Let A have arity k, then:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqada
% qaaiaadohacaWGVbGaamyBaiaadwgacaaMc8Uaam4yaiaad+gacaWG
% UbGaamizaiaadMgacaWG0bGaamyAaiaad+gacaWGUbGaaGPaVlaadI
% facqGHNis2daagaaqaamaadmaabaGaamyqaiabg2da9iaadAhadaWg
% aaWcbaGaaGymaaqabaGccqGHOiI2caWGbbGaeyypa0JaamODamaaBa
% aaleaacaaIYaaabeaakiabgIIiAlaac6cacaGGUaGaaiOlaiabgIIi
% AlaadgeacqGH9aqpcaWG2bWaaSbaaSqaaiaadUgaaeqaaaGccaGLBb
% GaayzxaaaaleaacaWGvbaakiaawIJ-aaGaayjkaiaawMcaaaqaaiab
% g2da9maabmaabaGaam4Caiaad+gacaWGTbGaamyzaiaaykW7caWGJb
% Gaam4Baiaad6gacaWGKbGaamyAaiaadshacaWGPbGaam4Baiaad6ga
% caaMc8UaamiwaaGaayjkaiaawMcaaaqaamaabmaabaGaam4Caiaad+
% gacaWGTbGaamyzaiaaykW7caWGJbGaam4Baiaad6gacaWGKbGaamyA
% aiaadshacaWGPbGaam4Baiaad6gacaaMc8UaamiwaiabgIIiApaaya
% aabaWaamWaaeaacaWGbbGaeyypa0JaamODamaaBaaaleaacaaIXaaa
% beaakiabgIIiAlaadgeacqGH9aqpcaWG2bWaaSbaaSqaaiaaikdaae
% qaaOGaeyikIOTaaiOlaiaac6cacaGGUaGaeyikIOTaamyqaiabg2da
% 9iaadAhadaWgaaWcbaGaam4AaaqabaaakiaawUfacaGLDbaaaSqaai
% aadwfaaOGaayjo+daacaGLOaGaayzkaaaabaGaeyypa0ZaaeWaaeaa
% caWGvbaacaGLOaGaayzkaaaaaaa!A18B!
\[
\begin{gathered}
\left( {some\,condition\,X \wedge \underbrace {\left[ {A = v_1 \vee A = v_2 \vee ... \vee A = v_k } \right]}_U} \right) \hfill \\
= \left( {some\,condition\,X} \right) \hfill \\
\left( {some\,condition\,X \vee \underbrace {\left[ {A = v_1 \vee A = v_2 \vee ... \vee A = v_k } \right]}_U} \right) \hfill \\
= \left( U \right) \hfill \\
\end{gathered}
\]](../latex_cache/9c1eb85805ac1e2a8627e5cf2bd4c22d.png)
You can think of the condition (U) as the definite TRUE 1.
Now we can begin the proof of the equality
![Formula: % MathType!MTEF!2!1!+-<br />
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm<br />
% aabaGaamOqaaGaayjkaiaawMcaaiabg2da9maaqahabaGaamiuamaa<br />
% bmaabaGaamOqaiaacYhacaWGbbGaeyypa0JaamODamaaBaaaleaaca<br />
% WGQbaabeaaaOGaayjkaiaawMcaaiaadcfadaqadaqaaiaadgeacqGH<br />
% 9aqpcaWG2bWaaSbaaSqaaiaadQgaaeqaaaGccaGLOaGaayzkaaaale<br />
% aacaWGQbGaeyypa0JaaGymaaqaaiaadUgaa0GaeyyeIuoaaaa!4E55!<br />
\[<br />
P\left( B \right) = \sum\limits_{j = 1}^k {P\left( {B|A = v_j } \right)P\left( {A = v_j } \right)} <br />
\]<br />](../latex_cache/62e60b9fc34d0d25c3a8afd94d6e714a.png)
using the Bayes Rule
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamyqaiaacYhacaWGcbaacaGLOaGaayzkaaGaeyypa0ZaaSaa
% aeaacaWGqbWaaeWaaeaacaWGbbGaey4jIKTaamOqaaGaayjkaiaawM
% caaaqaaiaadcfadaqadaqaaiaadkeaaiaawIcacaGLPaaaaaaaaa!44AC!
\[
P\left( {A|B} \right) = \frac{{P\left( {A \wedge B} \right)}}
{{P\left( B \right)}}
\]](../latex_cache/29924356dec9d1a162dd8d982e2dafeb.png)
we can convert the inference relation into intersection relation and rewrite RHS as:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaaeWb
% qaamaalaaabaGaamiuamaabmaabaGaamOqaiabgEIizlaadgeacqGH
% 9aqpcaWG2bWaaSbaaSqaaiaadQgaaeqaaaGccaGLOaGaayzkaaaaba
% GaamiuamaabmaabaGaamyqaiabg2da9iaadAhadaWgaaWcbaGaamOA
% aaqabaaakiaawIcacaGLPaaaaaGaamiuamaabmaabaGaamyqaiabg2
% da9iaadAhadaWgaaWcbaGaamOAaaqabaaakiaawIcacaGLPaaaaSqa
% aiaadQgacqGH9aqpcaaIXaaabaGaam4AaaqdcqGHris5aaGcbaGaey
% ypa0ZaaabCaeaacaWGqbWaaeWaaeaacaWGcbGaey4jIKTaamyqaiab
% g2da9iaadAhadaWgaaWcbaGaamOAaaqabaaakiaawIcacaGLPaaaaS
% qaaiaadQgacqGH9aqpcaaIXaaabaGaam4AaaqdcqGHris5aaaaaa!60EA!
\[
\begin{gathered}
\sum\limits_{j = 1}^k {\frac{{P\left( {B \wedge A = v_j } \right)}}
{{P\left( {A = v_j } \right)}}P\left( {A = v_j } \right)} \hfill \\
= \sum\limits_{j = 1}^k {P\left( {B \wedge A = v_j } \right)} \hfill \\
\end{gathered}
\]](../latex_cache/cfa46a10d4cd6d84560af43f0e320600.png)
using [6], this is nothing but:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb
% WaaeWaaeaacaWGcbGaey4jIK9aaGbaaeaadaWadaqaaiaadgeacqGH
% 9aqpcaWG2bWaaSbaaSqaaiaaigdaaeqaaOGaeyikIOTaamyqaiabg2
% da9iaadAhadaWgaaWcbaGaaGOmaaqabaGccqGHOiI2caGGUaGaaiOl
% aiaac6cacqGHOiI2caWGbbGaeyypa0JaamODamaaBaaaleaacaWGRb
% aabeaaaOGaay5waiaaw2faaaWcbaGaamyvaaGccaGL44paaiaawIca
% caGLPaaaaeaacqGH9aqpcaWGqbWaaeWaaeaacaWGcbaacaGLOaGaay
% zkaaaaaaa!5642!
\[
\begin{gathered}
P\left( {B \wedge \underbrace {\left[ {A = v_1 \vee A = v_2 \vee ... \vee A = v_k } \right]}_U} \right) \hfill \\
= P\left( B \right) \hfill \\
\end{gathered}
\]](../latex_cache/d3afe26131c9ddcb789dbe074c46a3bf.png)


