Coordination Numbers
September 3, 2009 Posted by Emre S. Tasci
Recently, we are working on liquid alloys and for our work, we need the coordination number distribution. It’s kind of a gray area when you talk about coordination number of atoms in a liquid but it’s better than nothing to understand the properties and even more. I’d like to write a log on the tools I’ve recently coded/used in order to refer to in the future if a similar situation occurs. Also, maybe there are some others conducting similar research so, the tools introduced here may be helpful to them.
Recently, while searching recent publications on liquid alloys, I’ve found a very good and resourceful article on liquid Na-K alloys by Dr. J.-F. Wax (“Molecular dynamics study of the static structure of liquid Na-K alloys”, Physica B 403 (2008) 4241-48 | doi:10.1016/j.physb.2008.09.014). In this paper, among other properties, he had also presented the partial pair distribution functions. Partial-pair distribution functions is the averaged probability that you’ll encounter an atom in r distance starting from another atom. In solid phase, due to the symmetry of the crystal structure, you have discrete values instead of a continuous distribution and everything is crystal clear but I guess that’s the price we pay dealing with liquids. 8)
Partial-pair distribution functions are very useful in the sense that they let you derive the bond-length between constituent atom species, corresponding to the first minimums of the plots. Hence, one can see the neighborhood ranges by just looking at the plots.
I’ve sent a mail to Dr. Wax explaining my research topics and my interest and asking for his research data to which he very kindly and generously replied by providing his data.
He had sent me a big file with numerous configurations (coordinates of the atoms) following each other. The first -and the simplest- task was to split the file into seperate configuration files via this bash script:
#!/bin/bash
# Script Name: split_POS4.sh
# Splits the NaK conf files compilation POS4_DAT into sepearate
# conf files.
# Emre S. Tasci <e.tasci@tudelft.nl>
# 01/09/09
linestart=2
p="p"
for (( i = 1; i <= 1000; i++ ))
do
echo $i;
lineend=$(expr $linestart + 2047)
confname=$(printf "%04d" $i)
echo -e "3\n2048" > $confname
sed -n "$linestart,$(echo $lineend$p)" POS4_DAT >> $confname
linestart=$(expr $lineend + 1)
cat $confname | qhull i TO $confname.hull
done
(The compilation was of 1000 configurations, each with 2048 atoms)
As you can check in the line before the “done” closer, I’ve -proudly- used Qhull software to calculate the convex hull of each configuration. A convex hull is the -hopefully minimum- shape that covers all your system. So, for each configuration I now had 2 files: “xxxx” (where xxxx is the id/number of the configuration set) storing the coordinates (preceded by 3 and 2048, corresponding to dimension and number of atoms information for the qhull to parse & process) and “xxxx.hull” file, generated by the qhull, containing the vertices list of each facet (preceded by the total number of facets).
A facet is (in 3D) the plane formed by the vertice points. Imagine a cube, where an atom lies at each corner, 3 in the inside. So, we can say that our system consists of 11 atoms and the minimal shape that has edges selected from system’s atoms and covering the whole is a cube, with the edges being the 8 atoms at the corners. Now, add an atom floating over the face at the top. Now the convex hull that wraps our new system would no longer be a 6-faced, 8-edged cube but a 9-faced, 9-edged polygon. I need to know the convex hull geometry in order to correctly calculate the coordination number distributions (details will follow shortly).
The aforementioned two files look like:
sururi@husniya hull_calcs $ head 0001
3
2048
0.95278770E+00 0.13334565E+02 0.13376155E+02
0.13025256E+02 0.87618381E+00 0.20168993E+01
0.12745038E+01 0.14068998E-01 0.22887323E+01
0.13066590E+02 0.20788591E+01 0.58119183E+01
0.10468218E+00 0.58523640E-01 0.64288678E+01
0.12839412E+02 0.13117012E+02 0.79093881E+01
0.11918105E+01 0.12163854E+02 0.10270868E+02
0.12673985E+02 0.11642538E+02 0.10514597E+02
sururi@husniya hull_calcs $ head 0001.hull
180
568 1127 1776
1992 104 1551
956 449 1026
632 391 1026
391 632 1543
391 956 1026
966 632 1026
966 15 1039
632 966 1039The sets of 3 numbers in the xxxx.hull file is the ids/numbers of the atoms forming the edges of the facets, i.e., they are the vertices.
To calculate the coordination number distribution, you need to pick each atom and then simply count the other atoms within the cut-off distance depending on your atom’s and the neighboring atom’s species. After you do the counting for every atom, you average the results and voilà ! there is your CN distribution. But here’s the catch: In order to be able to count properly, you must make sure that, your reference atom’s cutoff radii stay within your system — otherwise you’ll be undercounting. Suppose your reference atom is one of the atoms at the corners of the cube: It will (generally/approximately) lack 7/8 of the neighbouring atoms it would normally have if it was to be the center atom of the specimen/sample. Remember that we are studying a continuous liquid and trying to model the system via ensembles of samples. So we should omit these atoms which has neighborhoods outside of our systems. Since neighborhoods are defined through bond-length, we should only include the atoms with a distance to the outside of at least cut-off radii. The “outside” is defined as the region outside the convex hull and it’s designated by the facets (planes).
From the xxxx.hull file, we have the ids of the vertice atoms and their coordinates are stored in the xxxx file. To define the plane equation
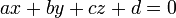
we will use the three vertice points, say p1, p2 and p3. From these 3 points, we calculate the normal n as:
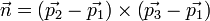
then, the plane equation (hence the coefficients a,b,c,d) can be derived by comparing the following equation:
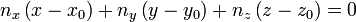
Here, (x0,y0,z0) are just the coordinates of any of the vertice points. And finally, the distance D between a point p1(x1,y1,z1) and a plane (a,b,c,d) is given by:
![D=\frac{\left|ax_{1}+by_{1}+cz_{1} \right|}{\sqrt[]{a^{2}+b^{2}+c^{2}}}](../tex/math/9167c920917483b1fb1d527814e55087.png)
Since vector operations are involved, I thought it’s better to do this job in Octave and wrote the following script that calculates the coefficients of the facets and then sets down to find out the points whose distances to all the facets are greater than the given cut-off radius:
sururi@husniya trunk $ cat octave_find_atoms_within.m
DummyA = 3;
%conf_index=292;
% Call from the command line like :
% octave -q --eval "Rcut=1.65;conf_index=293;path='$(pwd)';" octave_find_atoms_within.m
% hence specifying the conf_index at the command line.
% Emre S. Tasci <e.tasci@tudelft.nl> *
%
% From the positions and vertices file, calculates the plane
% equations (stored in "facet_coefficients") and then
% filters the atoms with respect to their distances to these
% facets. Writes the output to
% "hull_calcs/xxxx_insiders.txt" file
% 03/09/09 */
conf_index_name = num2str(sprintf("%04d",conf_index));;
%clock
clear facet_coefficients;
facet_coefficients = [];
global p v facet_coefficients
fp = fopen(strcat(path,"/hull_calcs/",conf_index_name));
k = fscanf(fp,"%d",2); % 1st is dim (=3), 2nd is number of atoms (=2048)
p = fscanf(fp,"%f",[k(1),k(2)]);
p = p';
fclose(fp);
%p = load("/tmp/del/delco");
fp = fopen(strcat(path,"/hull_calcs/",conf_index_name,".hull"));
k = fscanf(fp,"%d",1);% number of facets
v = fscanf(fp,"%d",[3,k]);
v = v';
fclose(fp);
%v = load("/tmp/del/delver");
function [a,b,c,d,e] = getPlaneCoefficients(facet_index)
global p v
% Get the 3 vertices
p1 = p(v(facet_index,1)+1,:); % The +1s come from the fact
p2 = p(v(facet_index,2)+1,:); % that qhull enumeration begins
p3 = p(v(facet_index,3)+1,:); % from 0 while Octave's from 1
%printf("%d: %f %f %f %f %f %f %f %f %f\n",facet_index,p1,p2,p3);
% Calculate the normal
n = cross((p2-p1),(p3-p1));
% Calculate the coefficients of the plane :
% ax + by + cz +d = 0
a = n(1);
b = n(2);
c = n(3);
d = -(dot(n,p1));
e = norm(n);
if(e==0)
printf("%f\n",p1);
printf("%f\n",p2);
printf("%f\n",p3);
printf("%d\n",facet_index);
endif
endfunction
function dist = distanceToPlane(point_index,facet_index)
global p facet_coefficients
k = facet_coefficients(facet_index,:);
n = [k(1) k(2) k(3)];
dist = abs(dot(n,p(point_index,:)) + k(4)) / k(5);
endfunction
for i = [1:size(v)(1)]
[a,b,c,d,e] = getPlaneCoefficients(i);
facet_coefficients = [ facet_coefficients ; [a,b,c,d,e]];
endfor
%Rcut = 1.65; % Defined from command line calling
% Find the points that are not closer than Rcut
inside_atoms = [];
for point = [1:size(p)(1)]
%for point = [1:100]
inside=true;
for facet = [1:size(v)(1)]
%for facet = [1:10]
%printf("%d - %d : %f\n",point,facet,dist);
if (distanceToPlane(point,facet)<Rcut)
inside = false;
break;
endif
endfor
if(inside)
inside_atoms = [inside_atoms point-1];
endif
endfor
fp = fopen(strcat(path,"/hull_calcs/",conf_index_name,"_insiders.txt"),"w");
fprintf(fp,"%d\n",inside_atoms);
fclose(fp);
%clock
This script is runned within the following php code which then takes the filtered atoms and does the counting using them:
<?PHP
/* Emre S. Tasci <e.tasci@tudelft.nl> *
*
* parse_configuration_data.php
*
* Written in order to parse the configuation files
* obtained from J.F. Wax in order to calculate the
* Coordination Number distribution. Each configuration
* file contain 2048 atoms' coordinates starting at the
* 3rd line. There is also a convex hull file generated
* using qhull (http://www.qhull.com) that contains the
* indexes (starting from 0) of the atoms that form the
* vertices of the convex hull. Finally there is the
* IP.dat file that identifies each atom (-1 for K; 1 for
* Na -- the second column is the relative masses).
*
* 02/09/09 */
/*
# if present, remove the previous run's results file
if(file_exists("results.txt"))
unlink("results.txt");
*/
error_reporting(E_ALL ^ E_NOTICE);
if(!file_exists("results.txt"))
{
$fp = fopen("results.txt","w");
fwrite($fp,"CONF#"."\tNa".implode("\tNa",range(1,20))."\tK".implode("\tK",range(1,20))."\n");
fclose($fp);
}
# Support for command line variable passing:
for($i=1;$i<sizeof($_SERVER["argv"]);$i++)
{
list($var0,$val0) = explode("=",$_SERVER["argv"][$i]);
$_GET[$var0] = $val0;
}
if($_GET["configuration"])
calculate($_GET["configuration"]);
else
exit("Please specify a configuration number [php parse_configuration_data.php configuration=xxx]\n");
function calculate($conf_index)
{
# Define the atoms array
$arr_atoms = Array();
# Get the information from the files
parse_types($arr_atoms);
$refs = get_vertices($conf_index);
parse_coordinates($arr_atoms,$conf_index);
# Define the Rcut-off values (obtained from partial parid distribution minimums)
$Rcut_arr = Array();
$Rscale = 3.828; # To convert reduced distances to Angstrom (if needed)
$Rscale = 1; # To convert reduced distances to Angstrom
$Rcut_arr["Na"]["Na"] = 1.38 * $Rscale;
$Rcut_arr["Na"]["K"] = 1.65 * $Rscale;
$Rcut_arr["K"]["Na"] = 1.65 * $Rscale;
$Rcut_arr["K"]["K"] = 1.52 * $Rscale;
$Rcut = $Rcut_arr["Na"]["K"]; # Taking the maximum one as the Rcut for safety
/*
# We have everything we need, so proceed to check
# if an atom is at safe distance wrt to the vertices
# Define all the ids
$arr_test_ids = range(0,2047);
# Subtract the ref atoms' ids
$arr_test_ids = array_diff($arr_test_ids, $refs);
sort($arr_test_ids);
//print_r($arr_test_ids);
$arr_passed_atom_ids = Array();
# Check each atom against refs
for($id=0, $size=sizeof($arr_test_ids); $id<$size; $id++)
{
//echo $id."\n";
$arr_atoms[$arr_test_ids[$id]]["in"] = TRUE;
foreach ($refs as $ref)
{
$distance = distance($arr_atoms[$arr_test_ids[$id]],$arr_atoms[$ref]);
//echo "\t".$ref."\t".$distance."\n";
if($distance < $Rcut)
{
$arr_atoms[$arr_test_ids[$id]]["in"] = FALSE;
break;
}
}
if($arr_atoms[$arr_test_ids[$id]]["in"] == TRUE)
$arr_passed_atom_ids[] = $arr_test_ids[$id];
}
*/
# Run the octave script file to calculate the inside atoms
if(!file_exists("hull_calcs/".sprintf("%04d",$conf_index)."_insiders.txt"))
exec("octave -q --eval \"Rcut=".$Rcut.";conf_index=".$conf_index.";path='$(pwd)';\" octave_find_atoms_within.m");
# Read the file generated by Octave
$arr_passed_atom_ids = file("hull_calcs/".sprintf("%04d",$conf_index)."_insiders.txt",FILE_IGNORE_NEW_LINES);
$arr_test_ids = range(0,2047);
$arr_test_ids = array_diff($arr_test_ids, $refs);
sort($arr_test_ids);
for($i=0, $size=sizeof($arr_test_ids);$i<$size;$i++)
$arr_atoms[$arr_test_ids[$i]]["in"]=FALSE;
# Begin checking every passed atom
foreach($arr_passed_atom_ids as $passed_atom_id)
{
$arr_atoms[$passed_atom_id]["in"] = TRUE;
for($i=0, $size=sizeof($arr_atoms); $i<$size; $i++)
{
$distance = distance($arr_atoms[$passed_atom_id],$arr_atoms[$i]);
//echo $passed_atom_id."\t---\t".$i."\n";
if($distance < $Rcut_arr[$arr_atoms[$passed_atom_id]["id"]][$arr_atoms[$i]["id"]] && $distance>0.001)
$arr_atoms[$passed_atom_id]["neighbour_count"] += 1;
}
}
# Do the binning
$CN_Na = Array();
$CN_K = Array();
for($i=0, $size=sizeof($arr_atoms); $i<$size; $i++)
{
if(array_key_exists("neighbour_count",$arr_atoms[$i]))
{
${"CN_".$arr_atoms[$i]['id']}[$arr_atoms[$i]["neighbour_count"]] += 1;
}
}
ksort($CN_Na);
ksort($CN_K);
//print_r($arr_atoms);
//print_r($CN_Na);
//print_r($CN_K);
# Report the results
$filename = "results/".sprintf("%04d",$conf_index)."_results.txt";
$fp = fopen($filename,"w");
fwrite($fp, "### Atoms array ###\n");
fwrite($fp,var_export($arr_atoms,TRUE)."\n");
fwrite($fp, "\n### CN Distribution for Na ###\n");
fwrite($fp,var_export($CN_Na,TRUE)."\n");
fwrite($fp, "\n### CN Distribution for K ###\n");
fwrite($fp,var_export($CN_K,TRUE)."\n");
# Percentage calculation:
$sum_Na = array_sum($CN_Na);
$sum_K = array_sum($CN_K);
foreach($CN_Na as $key=>$value)
$CN_Na[$key] = $value * 100 / $sum_Na;
foreach($CN_K as $key=>$value)
$CN_K[$key] = $value * 100 / $sum_K;
//print_r($CN_Na);
//print_r($CN_K);
fwrite($fp, "\n### CN Distribution (Percentage) for Na ###\n");
fwrite($fp,var_export($CN_Na,TRUE)."\n");
fwrite($fp, "\n### CN Distribution (Percentage) for K ###\n");
fwrite($fp,var_export($CN_K,TRUE)."\n");
fclose($fp);
# Write the summary to the results file
$fp = fopen("results.txt","a");
for($i=1;$i<=20;$i++)
{
if(!array_key_exists($i,$CN_Na))
$CN_Na[$i] = 0;
if(!array_key_exists($i,$CN_K))
$CN_K[$i] = 0;
}
ksort($CN_Na);
ksort($CN_K);
fwrite($fp,sprintf("%04d",$conf_index)."\t".implode("\t",$CN_Na)."\t".implode("\t",$CN_K)."\n");
fclose($fp);
}
function parse_types(&$arr_atoms)
{
# Parse the types
$i = 0;
$fp = fopen("IP.DAT", "r");
while(!feof($fp))
{
$line = fgets($fp,4096);
$auxarr = explode(" ",$line);
if($auxarr[0]==-1)
$arr_atoms[$i]["id"] = "Na";
else
$arr_atoms[$i]["id"] = "K";
$i++;
}
fclose($fp);
array_pop($arr_atoms);
return 0;
}
function get_vertices($conf_index)
{
$arr_refs = Array();
# Get the ids of the vertices of the convex hull
$filename = "hull_calcs/".sprintf("%04d",$conf_index).".hull";
$fp = fopen($filename, "r");
# Bypass the first line
$line = fgets($fp,4096);
while(!feof($fp))
{
$line = fgets($fp,4096);
$auxarr = explode(" ",$line);
array_pop($auxarr);
$arr_refs = array_merge($arr_refs, $auxarr);
}
fclose($fp);
// $arr_refs = array_unique($arr_refs); # This doesn't lose the keys
$arr_refs = array_keys(array_count_values($arr_refs)); # But this does.
return $arr_refs;
}
function parse_coordinates(&$arr_atoms, $conf_index)
{
# Parse the coordinates
$i = 0;
$filename = "hull_calcs/".sprintf("%04d",$conf_index);
$fp = fopen($filename, "r");
# Bypass the first two lines
$line = fgets($fp,4096);
$line = fgets($fp,4096);
while(!feof($fp))
{
$line = fgets($fp,4096);
$arr_atoms[$i]["coords"] = explode(" ",$line);
array_shift($arr_atoms[$i]["coords"]);
$i++;
}
fclose($fp);
array_pop($arr_atoms);
return 0;
}
function distance(&$atom1,&$atom2)
{
# Calculate the distance between the two atoms
$x1 = $atom1["coords"][0];
$x2 = $atom2["coords"][0];
$y1 = $atom1["coords"][1];
$y2 = $atom2["coords"][1];
$z1 = $atom1["coords"][2];
$z2 = $atom2["coords"][2];
return sqrt(pow($x1-$x2,2) + pow($y1-$y2,2) + pow($z1-$z2,2));
}
?>
The code above generates a “results/xxxx_results.txt” file containing all the information obtained in arrays format and also appends to “results.txt” file the relevant configuration file’s CN distribution summary. The systems can be visualized using the output generated by the following plotter.php script:
<?PHP
/* Emre S. Tasci <e.tasci@tudelft.nl> *
* Parses the results/xxxx_results.txt file and generates
* an XYZ file such that the atoms are labeled as the
* vertice atoms, close-vertice atoms and inside atoms..
* 02/09/09 */
# Support for command line variable passing:
for($i=1;$i<sizeof($_SERVER["argv"]);$i++)
{
list($var0,$val0) = explode("=",$_SERVER["argv"][$i]);
$_GET[$var0] = $val0;
}
if($_GET["configuration"])
$conf_index = $_GET["configuration"];
else
exit("Please specify a configuration number [php plotter.php configuration=xxx]\n");
$filename = sprintf("%04d",$conf_index);
# Get the atom array from the results file. Since results file
# contains other arrays as well, we slice the file using sed for the
# relevant part
$last_arr_line = exec('grep "### CN Distribution" results/'.$filename.'_results.txt -n -m1|sed "s:^\([0-9]\+\).*:\1:gi"');
exec('sed -n "2,'.($last_arr_line-1).'p" results/'.$filename.'_results.txt > system_tmp_array_dump_file');
$str=file_get_contents('system_tmp_array_dump_file');
$atom_arr=eval('return '.$str.';');
unlink('system_tmp_array_dump_file');
# Now that we have the coordinates, we itarate over the atoms to check
# the characteristic and designate them in the XYZ file.
$fp = fopen("system_".$filename.".xyz","w");
fwrite($fp,sizeof($atom_arr)."\n");
fwrite($fp,"Generated by plotter.php\n");
for($i=0, $size=sizeof($atom_arr);$i<$size;$i++)
{
if(!array_key_exists("in",$atom_arr[$i]))
$atomlabel = "Mg";#Vertices
elseif($atom_arr[$i]["in"]==TRUE)
$atomlabel = $atom_arr[$i]["id"];#Inside atoms
else
$atomlabel = "O";#Close-vertice atoms
fwrite($fp,$atomlabel."\t".implode("\t",$atom_arr[$i]["coords"]));
}
fclose($fp);
?>
which generates a “system_xxxx.xyz” file, ready to be viewed in a standard molecule viewing software. It designates the vertice atoms (of the convex hull, remember? 8)as “Mg” and the atoms close to them as “O” for easy-viewing purpose. A sample parsed file looks like this:
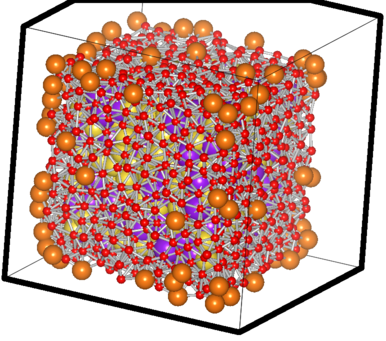
The filtered case of a sample Na-K system
The big orange atoms are the omitted vertice atoms; the small red ones are the atoms critically close to the facets and hence also omitted ones. You can see the purple and yellow atoms which have passed the test sitting happilly inside, with the counting done using them.. 8)



Leave a Reply