Some “trivial” derivations
December 4, 2007 Posted by Emre S. Tasci
Information Theory, Inference, and Learning Algorithms by David MacKay, Exercise 22.5:
A random variable x is assumed to have a probability distribution that is a mixture of two Gaussians,
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamiEaiaacYhacqaH8oqBdaWgaaWcbaGaaGymaaqabaGccaGG
% SaGaeqiVd02aaSbaaSqaaiaaikdaaeqaaOGaaiilaiabeo8aZbGaay
% jkaiaawMcaaiabg2da9maadmaabaWaaabCaeaacaWGWbWaaSbaaSqa
% aiaadUgaaeqaaOWaaSaaaeaacaaIXaaabaWaaOaaaeaacaaIYaGaeq
% iWdaNaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaqabaaaaOGaciyzaiaa
% cIhacaGGWbWaaeWaaeaacqGHsisldaWcaaqaamaabmaabaGaamiEai
% abgkHiTiabeY7aTnaaBaaaleaacaWGRbaabeaaaOGaayjkaiaawMca
% amaaCaaaleqabaGaaGOmaaaaaOqaaiaaikdacqaHdpWCdaahaaWcbe
% qaaiaaikdaaaaaaaGccaGLOaGaayzkaaaaleaacaWGRbGaeyypa0Ja
% aGymaaqaaiaaikdaa0GaeyyeIuoaaOGaay5waiaaw2faaaaa!63A5!
\[
P\left( {x|\mu _1 ,\mu _2 ,\sigma } \right) = \left[ {\sum\limits_{k = 1}^2 {p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x - \mu _k } \right)^2 }}
{{2\sigma ^2 }}} \right)} } \right]
\]](../latex_cache/02ffa24cafcda9c52b21f37689acad79.png)
where the two Gaussians are given the labels k = 1 and k = 2; the prior probability of the class label k is {p1 = 1/2, p2 = 1/2}; ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacq
% aH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawUhacaGL9baaaaa!3AFA!
\[
{\left\{ {\mu _k } \right\}}
\]](../latex_cache/63181a36e52687072bbbd54c4488895f.png) are the means of the two Gaussians; and both have standard deviation sigma. For brevity, we denote these parameters by
are the means of the two Gaussians; and both have standard deviation sigma. For brevity, we denote these parameters by
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCiUdiabgg
% Mi6oaacmaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam4Aaaqabaaa
% kiaawUhacaGL9baacaGGSaGaeq4WdmhacaGL7bGaayzFaaaaaa!42AB!
\[
{\mathbf{\theta }} \equiv \left\{ {\left\{ {\mu _k } \right\},\sigma } \right\}
\]](../latex_cache/0872f8d876f08afa90626cfb8bfd6165.png)
A data set consists of N points ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaaca
% WG4bWaaSbaaSqaaiaad6gaaeqaaaGccaGL7bGaayzFaaWaa0baaSqa
% aiaad6gacqGH9aqpcaaIXaaabaGaamOtaaaaaaa!3DF8!
\[
\left\{ {x_n } \right\}_{n = 1}^N
\]](../latex_cache/5960b3e63e93b0eadb7f05b6597dc081.png) which are assumed to be independent samples from the distribution. Let kn denote the unknown class label of the nth point.
which are assumed to be independent samples from the distribution. Let kn denote the unknown class label of the nth point.
Assuming that ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacq
% aH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawUhacaGL9baaaaa!3AFA!
\[
{\left\{ {\mu _k } \right\}}
\]](../latex_cache/63181a36e52687072bbbd54c4488895f.png) and
and ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdmhaaa!37B0!
\[
\sigma
\]](../latex_cache/0bcead44095f85d706d5bd0d3ee69019.png) are known, show that the posterior probability of the class label kn of the nth point can be written as
are known, show that the posterior probability of the class label kn of the nth point can be written as
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb
% WaaeWaaeaadaabcaqaaiaadUgadaWgaaWcbaGaamOBaaqabaGccqGH
% 9aqpcaaIXaaacaGLiWoacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaai
% ilaiaahI7aaiaawIcacaGLPaaacqGH9aqpdaWcaaqaaiaaigdaaeaa
% caaIXaGaey4kaSIaciyzaiaacIhacaGGWbWaamWaaeaacqGHsislda
% qadaqaaiabeM8a3naaBaaaleaacaaIXaaabeaakiaadIhadaWgaaWc
% baGaamOBaaqabaGccqGHRaWkcqaHjpWDdaWgaaWcbaGaaGimaaqaba
% aakiaawIcacaGLPaaaaiaawUfacaGLDbaaaaaabaGaamiuamaabmaa
% baWaaqGaaeaacaWGRbWaaSbaaSqaaiaad6gaaeqaaOGaeyypa0JaaG
% OmaaGaayjcSdGaamiEamaaBaaaleaacaWGUbaabeaakiaacYcacaWH
% 4oaacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaaIXaaabaGaaGymai
% abgUcaRiGacwgacaGG4bGaaiiCamaadmaabaGaey4kaSYaaeWaaeaa
% cqaHjpWDdaWgaaWcbaGaaGymaaqabaGccaWG4bWaaSbaaSqaaiaad6
% gaaeqaaOGaey4kaSIaeqyYdC3aaSbaaSqaaiaaicdaaeqaaaGccaGL
% OaGaayzkaaaacaGLBbGaayzxaaaaaaaaaa!7422!
\[
\begin{gathered}
P\left( {\left. {k_n = 1} \right|x_n ,{\mathbf{\theta }}} \right) = \frac{1}
{{1 + \exp \left[ { - \left( {\omega _1 x_n + \omega _0 } \right)} \right]}} \hfill \\
P\left( {\left. {k_n = 2} \right|x_n ,{\mathbf{\theta }}} \right) = \frac{1}
{{1 + \exp \left[ { + \left( {\omega _1 x_n + \omega _0 } \right)} \right]}} \hfill \\
\end{gathered}
\]](../latex_cache/f1256d14a59790f5d35c2bedc4a49bbc.png)
and give expressions for ![Formula: \[\omega _1 \]](../latex_cache/9b85d537fe39f505e5182913d97fdfb8.png) and
and ![Formula: \[\omega _0 \]](../latex_cache/dfa670f67ce3c9849cc5c143a295efac.png) .
.
Derivation:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaWaaqGaaeaacaWGRbWaaSbaaSqaaiaad6gaaeqaaOGaeyypa0Ja
% aGymaaGaayjcSdGaamiEamaaBaaaleaacaWGUbaabeaakiaacYcaca
% WH4oaacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaWGqbWaaeWaaeaa
% caWG4bWaaSbaaSqaaiaad6gaaeqaaOWaaqqaaeaacaWGRbWaaSbaaS
% qaaiaad6gaaeqaaOGaeyypa0JaaGymaiaacYcacaWH4oaacaGLhWoa
% aiaawIcacaGLPaaacaWGqbWaaeWaaeaacaWGRbWaaSbaaSqaaiaad6
% gaaeqaaOGaeyypa0JaaGymaaGaayjkaiaawMcaaaqaaiaadcfadaqa
% daqaaiaadIhadaWgaaWcbaGaamOBaaqabaaakiaawIcacaGLPaaaaa
% aaaa!598D!
\[
P\left( {\left. {k_n = 1} \right|x_n ,{\mathbf{\theta }}} \right) = \frac{{P\left( {x_n \left| {k_n = 1,{\mathbf{\theta }}} \right.} \right)P\left( {k_n = 1} \right)}}
{{P\left( {x_n } \right)}}
\]](../latex_cache/a715c20187b7d1333ddd7eac5d275abb.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamiEamaaBaaaleaacaWGUbaabeaakmaaeeaabaGaam4Aamaa
% BaaaleaacaWGUbaabeaakiabg2da9iaaigdacaGGSaGaaCiUdaGaay
% 5bSdaacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaaIXaaabaWaaOaa
% aeaacaaIYaGaeqiWdaNaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaqaba
% aaaOGaciyzaiaacIhacaGGWbWaaeWaaeaacqGHsisldaWcaaqaamaa
% bmaabaGaamiEamaaBaaaleaacaWGUbaabeaakiabgkHiTiabeY7aTn
% aaBaaaleaacaaIXaaabeaaaOGaayjkaiaawMcaamaaCaaaleqabaGa
% aGOmaaaaaOqaaiaaikdacqaHdpWCdaahaaWcbeqaaiaaikdaaaaaaa
% GccaGLOaGaayzkaaaaaa!59EC!
\[
P\left( {x_n \left| {k_n = 1,{\mathbf{\theta }}} \right.} \right) = \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x_n - \mu _1 } \right)^2 }}
{{2\sigma ^2 }}} \right)
\]](../latex_cache/fad7cf1dcafb714f7a176d734a527a09.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamiEamaaBaaaleaacaWGUbaabeaaaOGaayjkaiaawMcaaiab
% g2da9maaqahabaGaamiuamaabmaabaWaaqGaaeaacaWG4bWaaSbaaS
% qaaiaad6gaaeqaaaGccaGLiWoacaWGRbWaaSbaaSqaaiaad6gaaeqa
% aOGaeyypa0JaamyAaiaacYcacaWH4oaacaGLOaGaayzkaaGaamiuam
% aabmaabaGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaadMga
% aiaawIcacaGLPaaaaSqaaiaadMgacqGH9aqpcaaIXaaabaGaaGOmaa
% qdcqGHris5aaaa!53AA!
\[
P\left( {x_n } \right) = \sum\limits_{i = 1}^2 {P\left( {\left. {x_n } \right|k_n = i,{\mathbf{\theta }}} \right)P\left( {k_n = i} \right)}
\]](../latex_cache/4552f718d3d4a5d314db5eec6e935fe6.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb
% WaaeWaaeaadaabcaqaaiaadUgadaWgaaWcbaGaamOBaaqabaGccqGH
% 9aqpcaaIXaaacaGLiWoacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaai
% ilaiaahI7aaiaawIcacaGLPaaacqGH9aqpdaWcaaqaamaalaaabaGa
% aGymaaqaamaakaaabaGaaGOmaiabec8aWjabeo8aZnaaCaaaleqaba
% GaaGOmaaaaaeqaaaaakiGacwgacaGG4bGaaiiCamaabmaabaGaeyOe
% I0YaaSaaaeaadaqadaqaaiaadIhadaWgaaWcbaGaamOBaaqabaGccq
% GHsislcqaH8oqBdaWgaaWcbaGaaGymaaqabaaakiaawIcacaGLPaaa
% daahaaWcbeqaaiaaikdaaaaakeaacaaIYaGaeq4Wdm3aaWbaaSqabe
% aacaaIYaaaaaaaaOGaayjkaiaawMcaaiaadcfadaqadaqaaiaadUga
% daWgaaWcbaGaamOBaaqabaGccqGH9aqpcaaIXaaacaGLOaGaayzkaa
% aabaWaaSaaaeaacaaIXaaabaWaaOaaaeaacaaIYaGaeqiWdaNaeq4W
% dm3aaWbaaSqabeaacaaIYaaaaaqabaaaaOGaciyzaiaacIhacaGGWb
% WaaeWaaeaacqGHsisldaWcaaqaamaabmaabaGaamiEamaaBaaaleaa
% caWGUbaabeaakiabgkHiTiabeY7aTnaaBaaaleaacaaIXaaabeaaaO
% GaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaOqaaiaaikdacqaH
% dpWCdaahaaWcbeqaaiaaikdaaaaaaaGccaGLOaGaayzkaaGaamiuam
% aabmaabaGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaaigda
% aiaawIcacaGLPaaacqGHRaWkdaWcaaqaaiaaigdaaeaadaGcaaqaai
% aaikdacqaHapaCcqaHdpWCdaahaaWcbeqaaiaaikdaaaaabeaaaaGc
% ciGGLbGaaiiEaiaacchadaqadaqaaiabgkHiTmaalaaabaWaaeWaae
% aacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaeyOeI0IaeqiVd02aaSba
% aSqaaiaaikdaaeqaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaIYa
% aaaaGcbaGaaGOmaiabeo8aZnaaCaaaleqabaGaaGOmaaaaaaaakiaa
% wIcacaGLPaaacaWGqbWaaeWaaeaacaWGRbWaaSbaaSqaaiaad6gaae
% qaaOGaeyypa0JaaGOmaaGaayjkaiaawMcaaaaaaeaacqGH9aqpdaWc
% aaqaaiaaigdaaeaacaaIXaGaey4kaSIaciyzaiaacIhacaGGWbWaae
% WaaeaacqGHsisldaWcaaqaamaabmaabaGaamiEamaaBaaaleaacaWG
% UbaabeaakiabgkHiTiabeY7aTnaaBaaaleaacaaIYaaabeaaaOGaay
% jkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaOqaaiaaikdacqaHdpWC
% daahaaWcbeqaaiaaikdaaaaaaOGaey4kaSYaaSaaaeaadaqadaqaai
% aadIhadaWgaaWcbaGaamOBaaqabaGccqGHsislcqaH8oqBdaWgaaWc
% baGaaGymaaqabaaakiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaa
% aakeaacaaIYaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaaaOGaayjk
% aiaawMcaamaabmaabaWaaSaaaeaacaaIXaGaeyOeI0Iaamiuamaabm
% aabaGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaaigdaaiaa
% wIcacaGLPaaaaeaacaWGqbWaaeWaaeaacaWGRbWaaSbaaSqaaiaad6
% gaaeqaaOGaeyypa0JaaGymaaGaayjkaiaawMcaaaaaaiaawIcacaGL
% Paaaaaaaaaa!CC7A!
\[
\begin{gathered}
P\left( {\left. {k_n = 1} \right|x_n ,{\mathbf{\theta }}} \right) = \frac{{\frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x_n - \mu _1 } \right)^2 }}
{{2\sigma ^2 }}} \right)P\left( {k_n = 1} \right)}}
{{\frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x_n - \mu _1 } \right)^2 }}
{{2\sigma ^2 }}} \right)P\left( {k_n = 1} \right) + \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x_n - \mu _2 } \right)^2 }}
{{2\sigma ^2 }}} \right)P\left( {k_n = 2} \right)}} \hfill \\
= \frac{1}
{{1 + \exp \left( { - \frac{{\left( {x_n - \mu _2 } \right)^2 }}
{{2\sigma ^2 }} + \frac{{\left( {x_n - \mu _1 } \right)^2 }}
{{2\sigma ^2 }}} \right)\left( {\frac{{1 - P\left( {k_n = 1} \right)}}
{{P\left( {k_n = 1} \right)}}} \right)}} \hfill \\
\end{gathered}
\]](../latex_cache/1e6fdf2c5d24e2be5c59df57c14121ec.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS
% aaaeaacaaIXaaabaGaaGymaiabgUcaRiGacwgacaGG4bGaaiiCamaa
% dmaabaGaeyOeI0YaaeWaaeaadaqadaqaamaalaaabaWaaeWaaeaacq
% aH8oqBdaWgaaWcbaGaaGymaaqabaGccqGHsislcqaH8oqBdaWgaaWc
% baGaaGOmaaqabaaakiaawIcacaGLPaaaaeaacqaHdpWCdaahaaWcbe
% qaaiaaikdaaaaaaaGccaGLOaGaayzkaaGaamiEamaaBaaaleaacaWG
% UbaabeaakiabgUcaRmaabmaabaWaaSaaaeaadaqadaqaaiabeY7aTn
% aaBaaaleaacaaIYaaabeaakmaaCaaaleqabaGaaGOmaaaakiabgkHi
% TiabeY7aTnaaBaaaleaacaaIXaaabeaakmaaCaaaleqabaGaaGOmaa
% aaaOGaayjkaiaawMcaaaqaaiaaikdacqaHdpWCdaahaaWcbeqaaiaa
% ikdaaaaaaaGccaGLOaGaayzkaaaacaGLOaGaayzkaaaacaGLBbGaay
% zxaaaaaaaa!5E70!
\[
= \frac{1}
{{1 + \exp \left[ { - \left( {\left( {\frac{{\left( {\mu _1 - \mu _2 } \right)}}
{{\sigma ^2 }}} \right)x_n + \left( {\frac{{\left( {\mu _2 ^2 - \mu _1 ^2 } \right)}}
{{2\sigma ^2 }}} \right)} \right)} \right]}}
\]](../latex_cache/2cb3dc1005d19db77232acac5cfde110.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS
% aaaeaacaaIXaaabaGaaGymaiabgUcaRiGacwgacaGG4bGaaiiCamaa
% dmaabaGaeyOeI0YaaeWaaeaacqaHjpWDdaWgaaWcbaGaaGymaaqaba
% GccaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaey4kaSIaeqyYdC3aaSba
% aSqaaiaaicdaaeqaaaGccaGLOaGaayzkaaaacaGLBbGaayzxaaaaaa
% aa!4921!
\[
= \frac{1}
{{1 + \exp \left[ { - \left( {\omega _1 x_n + \omega _0 } \right)} \right]}}
\]](../latex_cache/fad0a283da2a75ecc80ae95039e225d9.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyYdC3aaS
% baaSqaaiaaigdaaeqaaOGaeyyyIO7aaSaaaeaadaqadaqaaiabeY7a
% TnaaBaaaleaacaaIXaaabeaakiabgkHiTiabeY7aTnaaBaaaleaaca
% aIYaaabeaaaOGaayjkaiaawMcaaaqaaiabeo8aZnaaCaaaleqabaGa
% aGOmaaaaaaGccaGG7aGaaCzcaiabeM8a3naaBaaaleaacaaIWaaabe
% aakiabggMi6oaalaaabaWaaeWaaeaacqaH8oqBdaWgaaWcbaGaaGOm
% aaqabaGcdaahaaWcbeqaaiaaikdaaaGccqGHsislcqaH8oqBdaWgaa
% WcbaGaaGymaaqabaGcdaahaaWcbeqaaiaaikdaaaaakiaawIcacaGL
% PaaaaeaacaaIYaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaaaaa!5809!
\[
\omega _1 \equiv \frac{{\left( {\mu _1 - \mu _2 } \right)}}
{{\sigma ^2 }}; & \omega _0 \equiv \frac{{\left( {\mu _2 ^2 - \mu _1 ^2 } \right)}}
{{2\sigma ^2 }}
\]](../latex_cache/ecb970e7b19db2f916b89d7f4f9ff62f.png)
Assume now that the means ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacq
% aH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawUhacaGL9baaaaa!3AFA!
\[
{\left\{ {\mu _k } \right\}}
\]](../latex_cache/63181a36e52687072bbbd54c4488895f.png) are not known, and that we wish to infer them from the data
are not known, and that we wish to infer them from the data ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaaca
% WG4bWaaSbaaSqaaiaad6gaaeqaaaGccaGL7bGaayzFaaWaa0baaSqa
% aiaad6gacqGH9aqpcaaIXaaabaGaamOtaaaaaaa!3DF8!
\[
\left\{ {x_n } \right\}_{n = 1}^N
\]](../latex_cache/5960b3e63e93b0eadb7f05b6597dc081.png) . (The standard deviation
. (The standard deviation ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdmhaaa!37B0!
\[
\sigma
\]](../latex_cache/0bcead44095f85d706d5bd0d3ee69019.png) is known.) In the remainder of this question we will derive an iterative algorithm for finding values for
is known.) In the remainder of this question we will derive an iterative algorithm for finding values for ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacq
% aH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawUhacaGL9baaaaa!3AFA!
\[
{\left\{ {\mu _k } \right\}}
\]](../latex_cache/63181a36e52687072bbbd54c4488895f.png) that maximize the likelihood,
that maximize the likelihood,
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaWaaiWaaeaacaWG4bWaaSbaaSqaaiaad6gaaeqaaaGccaGL7bGa
% ayzFaaWaa0baaSqaaiaad6gacqGH9aqpcaaIXaaabaGaamOtaaaakm
% aaeeaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam4Aaaqabaaakiaa
% wUhacaGL9baacaGGSaGaeq4WdmhacaGLhWoaaiaawIcacaGLPaaacq
% GH9aqpdaqeqbqaaiaadcfadaqadaqaaiaadIhadaWgaaWcbaGaamOB
% aaqabaGcdaabbaqaamaacmaabaGaeqiVd02aaSbaaSqaaiaadUgaae
% qaaaGccaGL7bGaayzFaaGaaiilaiabeo8aZbGaay5bSdaacaGLOaGa
% ayzkaaaaleaacaWGUbaabeqdcqGHpis1aOGaaiOlaaaa!5BD3!
\[
P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \prod\limits_n {P\left( {x_n \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right)} .
\]](../latex_cache/e8f09972b3500b374a1e5b0fd19ae615.png)
Let L denote the natural log of the likelihood. Show that the derivative of the log likelihood with respect to ![Formula: \[{\mu _k }\]](../latex_cache/8e114e04047dfd2df6cd90fecc90cc9d.png) is given by
is given by
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
% GHciITaeaacqGHciITcqaH8oqBdaWgaaWcbaGaam4AaaqabaaaaOGa
% amitaiabg2da9maaqafabaGaamiCamaaBaaaleaacaWGRbGaaiiFai
% aad6gaaeqaaOWaaSaaaeaadaqadaqaaiaadIhadaWgaaWcbaGaamOB
% aaqabaGccqGHsislcqaH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawI
% cacaGLPaaaaeaacqaHdpWCdaahaaWcbeqaaiaaikdaaaaaaOGaaiil
% aaWcbaGaamOBaaqab0GaeyyeIuoaaaa!4F8E!
\[
\frac{\partial }
{{\partial \mu _k }}L = \sum\limits_n {p_{k|n} \frac{{\left( {x_n - \mu _k } \right)}}
{{\sigma ^2 }},}
\]](../latex_cache/968180dae9f9ec36821998cd8cc198f2.png)
where ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
% aaleaacaWGRbGaaiiFaiaad6gaaeqaaOGaeyyyIORaamiuamaabmaa
% baGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaadUgadaabba
% qaaiaadIhadaWgaaWcbaGaamOBaaqabaGccaGGSaGaaCiUdaGaay5b
% SdaacaGLOaGaayzkaaaaaa!47DF!
\[
p_{k|n} \equiv P\left( {k_n = k\left| {x_n ,{\mathbf{\theta }}} \right.} \right)
\]](../latex_cache/1b5e0ed28e9818454709a25da45ef545.png) appeared above.
appeared above.
Derivation:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
% GHciITaeaacqGHciITcqaH8oqBdaWgaaWcbaGaam4AaaqabaaaaOGa
% ciiBaiaac6gacaWGqbWaaeWaaeaadaGadaqaaiaadIhadaWgaaWcba
% GaamOBaaqabaaakiaawUhacaGL9baadaqhaaWcbaGaamOBaiabg2da
% 9iaaigdaaeaacaWGobaaaOWaaqqaaeaadaGadaqaaiabeY7aTnaaBa
% aaleaacaWGRbaabeaaaOGaay5Eaiaaw2haaiaacYcacqaHdpWCaiaa
% wEa7aaGaayjkaiaawMcaaiabg2da9maalaaabaGaeyOaIylabaGaey
% OaIyRaeqiVd02aaSbaaSqaaiaadUgaaeqaaaaakmaaqafabaGaciiB
% aiaac6gacaWGqbWaaeWaaeaacaWG4bWaaSbaaSqaaiaad6gaaeqaaO
% WaaqqaaeaadaGadaqaaiabeY7aTnaaBaaaleaacaWGRbaabeaaaOGa
% ay5Eaiaaw2haaiaacYcacqaHdpWCaiaawEa7aaGaayjkaiaawMcaaa
% WcbaGaamOBaaqab0GaeyyeIuoaaaa!6A60!
\[
\frac{\partial }
{{\partial \mu _k }}\ln P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \frac{\partial }
{{\partial \mu _k }}\sum\limits_n {\ln P\left( {x_n \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right)}
\]](../latex_cache/d4fff688e4cb4a830395b148a0388ad0.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS
% aaaeaacqGHciITaeaacqGHciITcqaH8oqBdaWgaaWcbaGaam4Aaaqa
% baaaaOWaaabuaeaaciGGSbGaaiOBamaadmaabaWaaabuaeaacaWGWb
% WaaSbaaSqaaiaadUgaaeqaaOWaaSaaaeaacaaIXaaabaWaaOaaaeaa
% caaIYaGaeqiWdaNaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaqabaaaaO
% GaciyzaiaacIhacaGGWbWaamWaaeaacqGHsisldaWcaaqaamaabmaa
% baGaeqiVd02aaSbaaSqaaiaadUgaaeqaaOGaeyOeI0IaamiEamaaBa
% aaleaacaWGUbaabeaaaOGaayjkaiaawMcaamaaCaaaleqabaGaaGOm
% aaaaaOqaaiaaikdacqaHdpWCdaahaaWcbeqaaiaaikdaaaaaaaGcca
% GLBbGaayzxaaaaleaacaWGRbaabeqdcqGHris5aaGccaGLBbGaayzx
% aaaaleaacaWGUbaabeqdcqGHris5aaaa!6080!
\[
= \frac{\partial }
{{\partial \mu _k }}\sum\limits_n {\ln \left[ {\sum\limits_k {p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right]} } \right]}
\]](../latex_cache/86e7b4035c45e740407f4e2862f3fcca.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Zaaa
% buaeaadaWadaqaamaalaaabaGaamiCamaaBaaaleaacaWGRbaabeaa
% kmaalaaabaGaaGymaaqaamaakaaabaGaaGOmaiabec8aWjabeo8aZn
% aaCaaaleqabaGaaGOmaaaaaeqaaaaakmaalaaabaWaaeWaaeaacaWG
% 4bWaaSbaaSqaaiaad6gaaeqaaOGaeyOeI0IaeqiVd02aaSbaaSqaai
% aadUgaaeqaaaGccaGLOaGaayzkaaaabaGaeq4Wdm3aaWbaaSqabeaa
% caaIYaaaaaaakiGacwgacaGG4bGaaiiCamaadmaabaGaeyOeI0YaaS
% aaaeaadaqadaqaaiabeY7aTnaaBaaaleaacaWGRbaabeaakiabgkHi
% TiaadIhadaWgaaWcbaGaamOBaaqabaaakiaawIcacaGLPaaadaahaa
% WcbeqaaiaaikdaaaaakeaacaaIYaGaeq4Wdm3aaWbaaSqabeaacaaI
% YaaaaaaaaOGaay5waiaaw2faaaqaamaaqafabaGaamiCamaaBaaale
% aacaWGRbaabeaakmaalaaabaGaaGymaaqaamaakaaabaGaaGOmaiab
% ec8aWjabeo8aZnaaCaaaleqabaGaaGOmaaaaaeqaaaaakiGacwgaca
% GG4bGaaiiCamaadmaabaGaeyOeI0YaaSaaaeaadaqadaqaaiabeY7a
% TnaaBaaaleaacaWGRbaabeaakiabgkHiTiaadIhadaWgaaWcbaGaam
% OBaaqabaaakiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaakeaa
% caaIYaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaaaOGaay5waiaaw2
% faaaWcbaGaam4Aaaqab0GaeyyeIuoaaaaakiaawUfacaGLDbaaaSqa
% aiaad6gaaeqaniabggHiLdaaaa!7CFE!
\[
= \sum\limits_n {\left[ {\frac{{p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\frac{{\left( {x_n - \mu _k } \right)}}
{{\sigma ^2 }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right]}}
{{\sum\limits_k {p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right]} }}} \right]}
\]](../latex_cache/36d5d46d163b2f0805d07742b2476015.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaabuaeaaca
% WGWbWaaSbaaSqaaiaadUgaaeqaaOWaaSaaaeaacaaIXaaabaWaaOaa
% aeaacaaIYaGaeqiWdaNaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaqaba
% aaaOGaciyzaiaacIhacaGGWbWaamWaaeaacqGHsisldaWcaaqaamaa
% bmaabaGaeqiVd02aaSbaaSqaaiaadUgaaeqaaOGaeyOeI0IaamiEam
% aaBaaaleaacaWGUbaabeaaaOGaayjkaiaawMcaamaaCaaaleqabaGa
% aGOmaaaaaOqaaiaaikdacqaHdpWCdaahaaWcbeqaaiaaikdaaaaaaa
% GccaGLBbGaayzxaaaaleaacaWGRbaabeqdcqGHris5aOGaeyypa0Za
% aabuaeaacaWGqbWaaeWaaeaadaabcaqaaiaadIhadaWgaaWcbaGaam
% OBaaqabaaakiaawIa7aiaadUgadaWgaaWcbaGaamOBaaqabaGccqGH
% 9aqpcaWGPbGaaiilaiaahI7aaiaawIcacaGLPaaacaWGqbWaaeWaae
% aacaWGRbWaaSbaaSqaaiaad6gaaeqaaOGaeyypa0JaamyAaaGaayjk
% aiaawMcaaaWcbaGaamyAaaqab0GaeyyeIuoaaaa!6973!
\[
\sum\limits_k {p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right]} = \sum\limits_i {P\left( {\left. {x_n } \right|k_n = i,{\mathbf{\theta }}} \right)P\left( {k_n = i} \right)}
\]](../latex_cache/ac64de78a66933a927e697ce3399accb.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
% aaleaacaWGRbaabeaakmaalaaabaGaaGymaaqaamaakaaabaGaaGOm
% aiabec8aWjabeo8aZnaaCaaaleqabaGaaGOmaaaaaeqaaaaakiGacw
% gacaGG4bGaaiiCamaadmaabaGaeyOeI0YaaSaaaeaadaqadaqaaiab
% eY7aTnaaBaaaleaacaWGRbaabeaakiabgkHiTiaadIhadaWgaaWcba
% GaamOBaaqabaaakiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaa
% keaacaaIYaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaaaOGaay5wai
% aaw2faaiabg2da9iaadcfadaqadaqaaiaadUgadaWgaaWcbaGaamOB
% aaqabaGccqGH9aqpcaWGRbaacaGLOaGaayzkaaGaamiuamaabmaaba
% GaamiEamaaBaaaleaacaWGUbaabeaakmaaeeaabaGaam4AamaaBaaa
% leaacaWGUbaabeaakiabg2da9iaadUgacaGGSaGaaCiUdaGaay5bSd
% aacaGLOaGaayzkaaaaaa!6347!
\[
p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right] = P\left( {k_n = k} \right)P\left( {x_n \left| {k_n = k,{\mathbf{\theta }}} \right.} \right)
\]](../latex_cache/e7fad6f8f95484fb7540dd2f4a2fc8fc.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H49aaS
% aaaeaacqGHciITaeaacqGHciITcqaH8oqBdaWgaaWcbaGaam4Aaaqa
% baaaaOGaciiBaiaac6gacaWGqbWaaeWaaeaadaGadaqaaiaadIhada
% WgaaWcbaGaamOBaaqabaaakiaawUhacaGL9baadaqhaaWcbaGaamOB
% aiabg2da9iaaigdaaeaacaWGobaaaOWaaqqaaeaadaGadaqaaiabeY
% 7aTnaaBaaaleaacaWGRbaabeaaaOGaay5Eaiaaw2haaiaacYcacqaH
% dpWCaiaawEa7aaGaayjkaiaawMcaaiabg2da9maaqafabaWaaSaaae
% aacaWGqbWaaeWaaeaacaWGRbWaaSbaaSqaaiaad6gaaeqaaOGaeyyp
% a0Jaam4AaaGaayjkaiaawMcaaiaadcfadaqadaqaaiaadIhadaWgaa
% WcbaGaamOBaaqabaGcdaabbaqaaiaadUgadaWgaaWcbaGaamOBaaqa
% baGccqGH9aqpcaWGRbGaaiilaiaahI7aaiaawEa7aaGaayjkaiaawM
% caaaqaamaaqafabaGaamiuamaabmaabaWaaqGaaeaacaWG4bWaaSba
% aSqaaiaad6gaaeqaaaGccaGLiWoacaWGRbWaaSbaaSqaaiaad6gaae
% qaaOGaeyypa0JaamyAaiaacYcacaWH4oaacaGLOaGaayzkaaGaamiu
% amaabmaabaGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaadM
% gaaiaawIcacaGLPaaaaSqaaiaadMgaaeqaniabggHiLdaaaaWcbaGa
% amOBaaqab0GaeyyeIuoakmaalaaabaWaaeWaaeaacaWG4bWaaSbaaS
% qaaiaad6gaaeqaaOGaeyOeI0IaeqiVd02aaSbaaSqaaiaadUgaaeqa
% aaGccaGLOaGaayzkaaaabaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaa
% aaaaa!89F6!
\[
\Rightarrow \frac{\partial }
{{\partial \mu _k }}\ln P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \sum\limits_n {\frac{{P\left( {k_n = k} \right)P\left( {x_n \left| {k_n = k,{\mathbf{\theta }}} \right.} \right)}}
{{\sum\limits_i {P\left( {\left. {x_n } \right|k_n = i,{\mathbf{\theta }}} \right)P\left( {k_n = i} \right)} }}} \frac{{\left( {x_n - \mu _k } \right)}}
{{\sigma ^2 }}
\]](../latex_cache/2c3b479a4f50f6a32f51e3e0e2c7c833.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Zaaa
% buaeaacaWGWbWaaSbaaSqaaiaadUgacaGG8bGaamOBaaqabaaabaGa
% amOBaaqab0GaeyyeIuoakmaalaaabaWaaeWaaeaacaWG4bWaaSbaaS
% qaaiaad6gaaeqaaOGaeyOeI0IaeqiVd02aaSbaaSqaaiaadUgaaeqa
% aaGccaGLOaGaayzkaaaabaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaa
% aaaaa!4840!
\[
= \sum\limits_n {p_{k|n} } \frac{{\left( {x_n - \mu _k } \right)}}
{{\sigma ^2 }}
\]](../latex_cache/c8011d7a11739ee0738f1c36b33e36ea.png)
Assuming that ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdmhaaa!37B0!
\[
\sigma
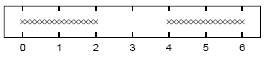
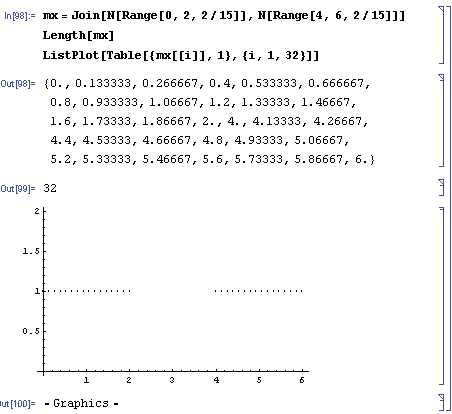
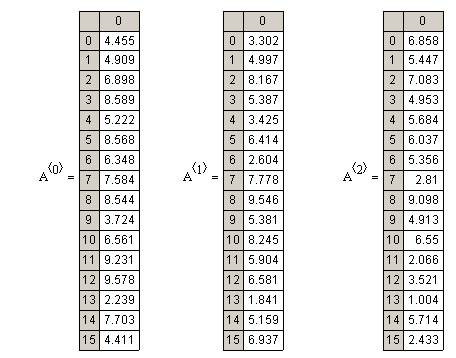
\]](../latex_cache/0bcead44095f85d706d5bd0d3ee69019.png) =1, sketch a contour plot of the likelihood function as a function of mu1 and mu2 for the data set shown above. The data set consists of 32 points. Describe the peaks in your sketch and indicate their widths.
=1, sketch a contour plot of the likelihood function as a function of mu1 and mu2 for the data set shown above. The data set consists of 32 points. Describe the peaks in your sketch and indicate their widths.
Solution:
We will be trying to plot the function
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaWaaiWaaeaacaWG4bWaaSbaaSqaaiaad6gaaeqaaaGccaGL7bGa
% ayzFaaWaa0baaSqaaiaad6gacqGH9aqpcaaIXaaabaGaamOtaaaakm
% aaeeaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam4Aaaqabaaakiaa
% wUhacaGL9baacaGGSaGaeq4WdmNaeyypa0JaaGymaaGaay5bSdaaca
% GLOaGaayzkaaaaaa!4B35!
\[
P\left( {\left\{ {x_n } \right\}_{n = 1}^32 \left| {\left\{ {\mu _k } \right\},\sigma = 1} \right.} \right)
\]](../latex_cache/71b40c661f5c9db63270e0e74a946f2e.png)
if we designate the function
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca
% aIXaaabaWaaOaaaeaacaaIYaGaeqiWdahaleqaaaaakiGacwgacaGG
% 4bGaaiiCamaabmaabaGaeyOeI0YaaSaaaeaadaqadaqaaiaadIhacq
% GHsislcqaH8oqBaiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaa
% keaacaaIYaaaaaGaayjkaiaawMcaaaaa!458F!
\[
{\frac{1}
{{\sqrt {2\pi } }}\exp \left( { - \frac{{\left( {x - \mu } \right)^2 }}
{2}} \right)}
\]](../latex_cache/2ad62d34e3684874733b4cb33953d5d3.png)
as p[x,mu] (remember that ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdmhaaa!37B0!
\[
\sigma
\]](../latex_cache/0bcead44095f85d706d5bd0d3ee69019.png) =1 and
=1 and ![Formula: \[\frac{1}{{\sqrt {2\pi } }} = {\text{0}}{\text{.3989422804014327}}\]](../latex_cache/3007395e2c673cf6173195f8f616e34e.png) ),
),
![Formula: % MathType!MTEF!2!1!+-<br />
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb<br />
% WaaeWaaeaacaWG4bGaaiiFamaacmaabaGaeqiVd0gacaGL7bGaayzF<br />
% aaGaaiilaiabeo8aZbGaayjkaiaawMcaaiabg2da9maadmaabaWaaa<br />
% bCaeaadaqadaqaaiaadchadaWgaaWcbaGaam4AaaqabaGccqGH9aqp<br />
% caGGUaGaaGynaaGaayjkaiaawMcaamaalaaabaGaaGymaaqaamaaka<br />
% aabaGaaGOmaiabec8aWnaabmaabaGaeq4Wdm3aaWbaaSqabeaacaaI<br />
% YaaaaOGaeyypa0JaaGymamaaCaaaleqabaGaaGOmaaaaaOGaayjkai<br />
% aawMcaaaWcbeaaaaGcciGGLbGaaiiEaiaacchadaqadaqaaiabgkHi<br />
% TmaalaaabaWaaeWaaeaacaWG4bGaeyOeI0IaeqiVd02aaSbaaSqaai<br />
% aadUgaaeqaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaaGc<br />
% baGaaGOmaiabeo8aZnaaCaaaleqabaGaaGOmaaaaaaaakiaawIcaca<br />
% GLPaaaaSqaaiaadUgacqGH9aqpcaaIXaaabaGaaGOmaaqdcqGHris5<br />
% aaGccaGLBbGaayzxaaaabaGaeyypa0JaaiOlaiaaiwdadaqadaqaai<br />
% aahchadaWadaqaaiaadIhacaGGSaGaamyBaiaadwhacaaIXaaacaGL<br />
% BbGaayzxaaGaey4kaSIaaCiCamaadmaabaGaamiEaiaacYcacaWGTb<br />
% GaamyDaiaaikdaaiaawUfacaGLDbaaaiaawIcacaGLPaaacqGHHjIU<br />
% caWHWbGaaCiCamaadmaabaGaamiEaiaacYcacaWGTbGaamyDaiaaig<br />
% dacaGGSaGaamyBaiaadwhacaaIYaaacaGLBbGaayzxaaaaaaa!8AA0!<br />
\[<br />
\begin{gathered}<br />
P\left( {x|\left\{ \mu \right\},\sigma } \right) = \left[ {\sum\limits_{k = 1}^2 {\left( {p_k = .5} \right)\frac{1}<br />
{{\sqrt {2\pi \left( {\sigma ^2 = 1^2 } \right)} }}\exp \left( { - \frac{{\left( {x - \mu _k } \right)^2 }}<br />
{{2\sigma ^2 }}} \right)} } \right] \hfill \\<br />
= .5\left( {{\mathbf{p}}\left[ {x,mu1} \right] + {\mathbf{p}}\left[ {x,mu2} \right]} \right) \equiv {\mathbf{pp}}\left[ {x,mu1,mu2} \right] \hfill \\ <br />
\end{gathered} <br />
\]](../latex_cache/d8547ac7bb53e78258a1e9e9b6404ee4.png)
![Formula: % MathType!MTEF!2!1!+-<br />
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb<br />
% WaaeWaaeaadaGadaqaaiaadIhadaWgaaWcbaGaamOBaaqabaaakiaa<br />
% wUhacaGL9baadaqhaaWcbaGaamOBaiabg2da9iaaigdaaeaacaWGob<br />
% aaaOWaaqqaaeaadaGadaqaaiabeY7aTnaaBaaaleaacaWGRbaabeaa<br />
% aOGaay5Eaiaaw2haaiaacYcacqaHdpWCaiaawEa7aaGaayjkaiaawM<br />
% caaiabg2da9maarafabaGaamiuamaabmaabaGaamiEamaaBaaaleaa<br />
% caWGUbaabeaakmaaeeaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam<br />
% 4AaaqabaaakiaawUhacaGL9baacaGGSaGaeq4WdmhacaGLhWoaaiaa<br />
% wIcacaGLPaaaaSqaaiaad6gaaeqaniabg+GivdaakeaacqGH9aqpda<br />
% qeqbqaaiaahchacaWHWbWaamWaaeaacaWG4bGaaiilaiaad2gacaWG<br />
% 1bGaaGymaiaacYcacaWGTbGaamyDaiaaikdaaiaawUfacaGLDbaaaS<br />
% qaaiaad6gaaeqaniabg+GivdGccqGHHjIUcaWHWbGaaCiCaiaahcha<br />
% daWadaqaaiaadIhacaGGSaGaamyBaiaadwhacaaIXaGaaiilaiaad2<br />
% gacaWG1bGaaGOmaaGaay5waiaaw2faaaaaaa!791F!<br />
\[<br />
\begin{gathered}<br />
P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \prod\limits_n {P\left( {x_n \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right)} \hfill \\<br />
= \prod\limits_n {{\mathbf{pp}}\left[ {x,mu1,mu2} \right]} \equiv {\mathbf{ppp}}\left[ {x,mu1,mu2} \right] \hfill \\ <br />
\end{gathered} <br />
\]](../latex_cache/45d43b605033a4aa279f5db4b6c5f8cb.png)
then we have:
![Formula: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb<br />% WaaeWaaeaadaGadaqaaiaadIhadaWgaaWcbaGaamOBaaqabaaakiaa<br />% wUhacaGL9baadaqhaaWcbaGaamOBaiabg2da9iaaigdaaeaacaWGob<br />% aaaOWaaqqaaeaadaGadaqaaiabeY7aTnaaBaaaleaacaWGRbaabeaa<br />% aOGaay5Eaiaaw2haaiaacYcacqaHdpWCaiaawEa7aaGaayjkaiaawM<br />% caaiabg2da9maarafabaGaamiuamaabmaabaGaamiEamaaBaaaleaa<br />% caWGUbaabeaakmaaeeaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam<br />% 4AaaqabaaakiaawUhacaGL9baacaGGSaGaeq4WdmhacaGLhWoaaiaa<br />% wIcacaGLPaaaaSqaaiaad6gaaeqaniabg+GivdaakeaacqGH9aqpda<br />% qeqbqaaiaahchacaWHWbWaamWaaeaacaWG4bGaaiilaiaad2gacaWG<br />% 1bGaaGymaiaacYcacaWGTbGaamyDaiaaikdaaiaawUfacaGLDbaaaS<br />% qaaiaad6gaaeqaniabg+GivdGccqGHHjIUcaWHWbGaaCiCaiaahcha<br />% daWadaqaaiaadIhacaGGSaGaamyBaiaadwhacaaIXaGaaiilaiaad2<br />% gacaWG1bGaaGOmaaGaay5waiaaw2faaaaaaa!791F!<br />\[<br />\begin{gathered}<br /> P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \prod\limits_n {P\left( {x_n \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right)} \hfill \\<br /> = \prod\limits_n {{\mathbf{pp}}\left[ {x,mu1,mu2} \right]} \equiv {\mathbf{ppp}}\left[ {x,mu1,mu2} \right] \hfill \\ <br />\end{gathered} <br />\]](../latex_cache/45d43b605033a4aa279f5db4b6c5f8cb.png)
And in Mathematica, these mean:
mx=Join[N[Range[0,2,2/15]],N[Range[4,6,2/15]]]
Length[mx]
ListPlot[Table[{mx[[i]],1},{i,1,32}]]
p[x_,mu_]:=0.3989422804014327` * Exp[-(mu-x)^2/2];
pp[x_,mu1_,mu2_]:=.5 (p[x,mu1]+p[x,mu2]);
ppp[xx_,mu1_,mu2_]:=Module[
{ptot=1},
For[i=1,i<=Length[xx],i++,
ppar = pp[xx[[i]],mu1,mu2];
ptot *= ppar;
(*Print[xx[[i]],"\t",ppar];*)
];
Return[ptot];
];
Plot3D[ppp[mx,mu1,mu2],{mu1,0,6},{mu2,0,6},PlotRange->{0,10^-25}];

ContourPlot[ppp[mx,mu1,mu2],{mu1,0,6},{mu2,0,6},{PlotRange->{0,10^-25},ContourLines->False,PlotPoints->250}];(*It may take a while with PlotPoints->250, so just begin with PlotPoints->25 *)
That’s all folks! (for today I guess 8) (and also, I know that I said next entry would be about the soft K-means two entries ago, but believe me, we’re coming to that, eventually 😉
Attachments: Mathematica notebook for this entry, MSWord Document (actually this one is intended for me, because in the future I may need them again)
Likelihood of Gaussian(s) – Scrap Notes
December 3, 2007 Posted by Emre S. Tasci
Given a set of N data x, ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaaca
% WG4baacaGL7bGaayzFaaWaa0baaSqaaiaadMgacqGH9aqpcaaIXaaa
% baGaamOtaaaaaaa!3CCA!
\[
{\left\{ x \right\}_{i = 1}^N }
\]](../latex_cache/36f475828683a171a142690beecf0de0.png) , the optimal parameters for a Gaussian Probability Distribution Function defined as:
, the optimal parameters for a Gaussian Probability Distribution Function defined as:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6
% gadaWadaqaaiGaccfadaqadaqaamaaeiaabaWaaiWaaeaacaWG4baa
% caGL7bGaayzFaaWaa0baaSqaaiaadMgacqGH9aqpcaaIXaaabaGaam
% OtaaaaaOGaayjcSdGaeqiVd0Maaiilaiabeo8aZbGaayjkaiaawMca
% aaGaay5waiaaw2faaiabg2da9iabgkHiTiaad6eaciGGSbGaaiOBam
% aabmaabaWaaOaaaeaacaaIYaGaeqiWdahaleqaaOGaeq4WdmhacaGL
% OaGaayzkaaGaeyOeI0YaaSGbaeaadaWadaqaaiaad6eadaqadaqaai
% abeY7aTjabgkHiTiqadIhagaqeaaGaayjkaiaawMcaamaaCaaaleqa
% baGaaGOmaaaakiabgUcaRiaadofaaiaawUfacaGLDbaaaeaacaaIYa
% Gaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaaaaa!627A!
\[
\ln \left[ {\operatorname{P} \left( {\left. {\left\{ x \right\}_{i = 1}^N } \right|\mu ,\sigma } \right)} \right] = - N\ln \left( {\sqrt {2\pi } \sigma } \right) - {{\left[ {N\left( {\mu - \bar x} \right)^2 + S} \right]} \mathord{\left/
{\vphantom {{\left[ {N\left( {\mu - \bar x} \right)^2 + S} \right]} {2\sigma ^2 }}} \right.
\kern-\nulldelimiterspace} {2\sigma ^2 }}
\]](../latex_cache/2263a9a9668dc98fdb36e2a16e2f7d17.png)
are:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacq
% aH8oqBcaGGSaGaeq4WdmhacaGL7bGaayzFaaWaaSbaaSqaaiaad2ea
% caWGHbGaamiEaiaadMgacaWGTbGaamyDaiaad2gacaWGmbGaamyAai
% aadUgacaWGLbGaamiBaiaadMgacaWGObGaam4Baiaad+gacaWGKbaa
% beaakiabg2da9maacmaabaGabmiEayaaraGaaiilamaakaaabaWaaS
% GbaeaacaWGtbaabaGaamOtaaaaaSqabaaakiaawUhacaGL9baaaaa!5316!
\[
\left\{ {\mu ,\sigma } \right\}_{MaximumLikelihood} = \left\{ {\bar x,\sqrt {{S \mathord{\left/
{\vphantom {S N}} \right.
\kern-\nulldelimiterspace} N}} } \right\}
\]](../latex_cache/fb38a9b5139084cb4210f812c71f9232.png)
with the definitions
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmiEayaara
% Gaeyypa0ZaaSaaaeaadaaeWbqaaiaadIhadaWgaaWcbaGaamOBaaqa
% baaabaGaamOBaiabg2da9iaaigdaaeaacaWGobaaniabggHiLdaake
% aacaWGobaaaiaacYcacaWLjaGaam4uaiabg2da9maaqahabaWaaeWa
% aeaacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaeyOeI0IabmiEayaara
% aacaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaaqaaiaad6gacqGH
% 9aqpcaaIXaaabaGaamOtaaqdcqGHris5aaaa!5057!
\[
\bar x = \frac{{\sum\limits_{n = 1}^N {x_n } }}
{N}, & S = \sum\limits_{n = 1}^N {\left( {x_n - \bar x} \right)^2 }
\]](../latex_cache/2306d354e1dd738ba188a23c0295b260.png)
Let’s see this in an example:
Define the data set mx:
mx={1,7,9,10,15}
Calculate the optimal mu and sigma:
dN=Length[mx];
mu=Sum[mx[[i]]/dN,{i,1,dN}];
sig =Sqrt[Sum[(mx[[i]]-mu)^2,{i,1,dN}]/dN];
Print["mu = ",N[mu]];
Print["sigma = ",N[sig]];
Now, let’s see this Gaussian Distribution Function:
<<Statistics`NormalDistribution`
ndist=NormalDistribution[mu,sig];
MultipleListPlot[Table[{x,PDF[NormalDistribution[mu,sig],x]}, {x,0,20,.04}],Table[{mx[[i]], PDF[NormalDistribution[mu,sig],mx[[i]]]},{i,5}], {PlotRange->{Automatic,{0,.1}},PlotJoined->{False,False}, SymbolStyle->{GrayLevel[.8],GrayLevel[0]}}]
.png)

3D Scatter Plot of data read from a file
November 29, 2007 Posted by Emre S. Tasci
We’re soon going to need this information when playing a game called clustering so, it’s handy to have this around.
Suppose that the data belong to the positions of some number of particles given in Cartesian coordinates. The file (let’s assume it resides in the root of the d drive, having the name "lol1.txt") looks something similar to this:
4.455 3.302 6.858
4.909 4.997 5.447
6.898 8.167 7.083
8.589 5.387 4.953
5.222 3.425 5.684
8.568 6.414 6.037
6.348 2.604 5.356
7.584 7.778 2.810
8.544 9.546 9.098
3.724 5.381 4.913
6.561 8.245 6.550
9.231 5.904 2.066
9.578 6.581 3.521
2.239 1.841 1.004
7.703 5.159 5.714
4.411 6.937 2.433
First, let’s try it in Mathematica:
m=OpenRead["d:\lol1.txt"];
k= ReadList[m,Number];
Close[m];
(k =Partition[k,3]) // TableForm
(* And you can definitely Plot it too *)
<<Graphics`Graphics3D`
PlotStyle->{{PointSize[0.04],GrayLevel[0.09]}}]
Actually, I just copied the above code from a previous entry (but I had updated it just yesterday, so it is still fresh) the output graph will look like this:
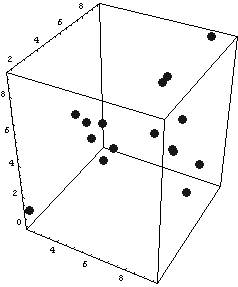
It is not that much practical to change the view angle (or most probably I don’t know how to do it) using Mathematica…
You can, for example, try something like this:
For[i=1,i<10,i+=1,ScatterPlot3D[k,PlotStyle->{{PointSize[0.04],GrayLevel[0.09]}},ViewPoint->{-2,i,2},AxesLabel->{"x","y","z"}]]
Or, if you have Mathcad with you, you can do this much simpler and more enjoyable way, too (but be warned, if I believed that Mathcad was superior to Mathematica, I would have a category for Mathcad instead of Mathematica category I’m having now – Mathcad actually from time to time makes you want to bite the keyboard! ;)! I decided to use Mathcad to visualize my scatter pattern and at once realized that, it has been nearly 5 years since I last used it. My favourite package used to be MapleV but -in my opinion- the Waterloo guys just tore it down when they switched the code language to Java. That was when our ways parted. Maple had nice graphics feature, too. So, if you’re using please send me your version of this entry… So, back to Mathcad:
First, from the "Insert…" menu, select "Component", then "File Read or Write" as the type and then select "Read from file". Browse to the designated file and make sure that "Use comma as decimal symbol" is unchecked since we’re using "." for the seperator. By the way, I’m using Mathcad2001 so it may (may?! more like surely!) be a little bit different about the options…
Attach a symbol to this file, say A so that now we have smt like:

Now, just for the fun of it, define another set like:
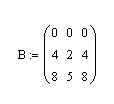
You may also check your data if you want:
Now define a 3D Scatter Plot either from the Graph Pallette, or more preferably from the Insert menu:
Fill in the data section of the plot as (A<0>,A<1>,A<2>),(B<0>,B<1>,B<2>) and it’s all yours!
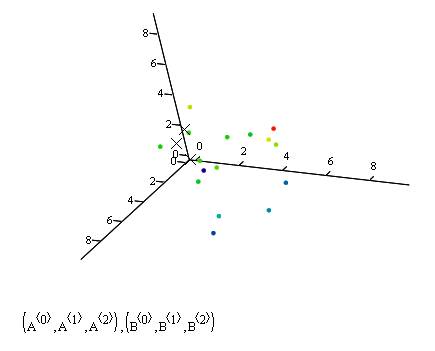
With mathcad I was able to rotate the graph whichever way I wanted and also could easily include data from different sources (like the A and B in the example) and plot them any way I wanted to. Here are the snapshots from a more "cute" plot with 500 data points:
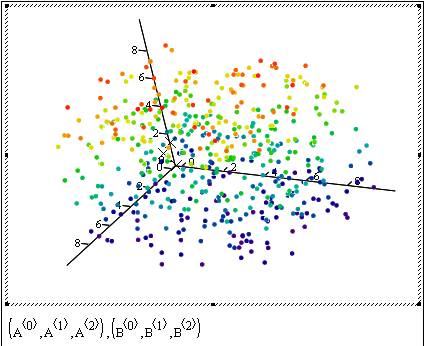
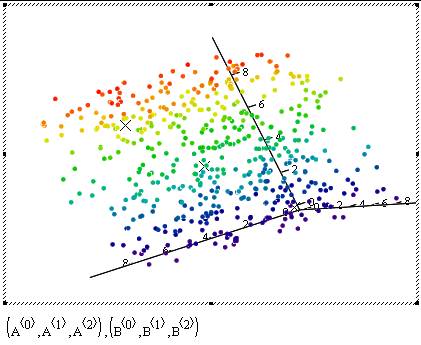
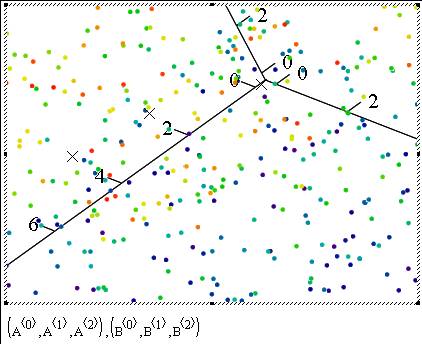
Hint for our game to be announced: Let’s call the little points in the plot as data’s and the Xs as "K-Means"
(7,4) Hamming Code
November 23, 2007 Posted by Emre S. Tasci
The (7,4) Hamming Code is a system that is used for sending bits of block length 4 (16 symbols) with redundancy resulting in transmission of blocks of 7 bits length. The first 4 bits of the transmitted information contains the original source bits and the last three contains the parity-check bits for {1,2,3}, {2,3,4} and {1,3,4} bits.
It has a transmission rate of 4/7 ~ 0.57 . Designate the source block as s, the transmission operator as G so that transmitted block t is t = GTs and parity check operator is designated as H where:
![Formula: % MathType!MTEF!2!1!+-<br> % feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br> % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br> % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br> % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br> % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCisaiabg2<br> % da9maadmaabaqbaeaGboWbaaaabaGaaGymaaqaaiaaigdaaeaacaaI<br> % XaaabaGaaGimaaqaaiaaigdaaeaacaaIWaaabaGaaGimaaqaaiaaic<br> % daaeaacaaIXaaabaGaaGymaaqaaiaaigdaaeaacaaIWaaabaGaaGym<br> % aaqaaiaaicdaaeaacaaIXaaabaGaaGimaaqaaiaaigdaaeaacaaIXa<br> % aabaGaaGimaaqaaiaaicdaaeaacaaIXaaaaaGaay5waiaaw2faaaaa<br> % !4A2B!<br> ${\bf{H}} = \left[ {\begin{array}{*{20}c}<br> 1 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\<br> 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\<br> 1 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\<br> \end{array}} \right]$<br>](../latex_cache/4588c14c4af56a662e011f912cd8a4b7.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCiuaiabg2
% da9maadmaabaqbaeaGboabaaaabaGaaGymaaqaaiaaigdaaeaacaaI
% XaaabaGaaGimaaqaaiaaicdaaeaacaaIXaaabaGaaGymaaqaaiaaig
% daaeaacaaIXaaabaGaaGimaaqaaiaaigdaaeaacaaIXaaaaaGaay5w
% aiaaw2faaaaa!4399!
\[
{\mathbf{P}} = \left[ {\begin{array}{*{20}c}
1 \hfill & 1 \hfill & 1 \hfill & 0 \hfill \\
0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\
1 \hfill & 0 \hfill & 1 \hfill & 1 \hfill \\
\end{array} } \right]
\]](../latex_cache/672a07f960375e53a05a3340ef147c53.png)
As it calculates the parities for bits, also its Modulo wrt 2 must be included. Since we’re calculating the parities for {1,2,3}, {2,3,4} and {1,3,4} bit-groups, the values of the P are easily understandable. Now, we will join the Identity Matrix of order 4 (for directly copying the first 4 values) with the P operator to construct the GT transformation (encoder) operator:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaC4ramaaCa
% aaleqabaGaamivaaaakiabg2da9maadmaabaqbaeaGbEabaaaaaeaa
% caaIXaaabaGaaGimaaqaaiaaicdaaeaacaaIWaaabaGaaGOmaaqaai
% aaigdaaeaacaaIWaaabaGaaGimaaqaaiaaicdaaeaacaaIWaaabaGa
% aGymaaqaaiaaicdaaeaacaaIWaaabaGaaGimaaqaaiaaicdaaeaaca
% aIXaaabaGaaGymaaqaaiaaigdaaeaacaaIXaaabaGaaGimaaqaaiaa
% icdaaeaacaaIXaaabaGaaGymaaqaaiaaigdaaeaacaaIXaaabaGaaG
% imaaqaaiaaigdaaeaacaaIXaaaaaGaay5waiaaw2faaaaa!505A!
\[
{\mathbf{G}}^T = \left[ {\begin{array}{*{20}c}
1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\
0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\
0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\
0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\
1 \hfill & 1 \hfill & 1 \hfill & 0 \hfill \\
0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\
1 \hfill & 0 \hfill & 1 \hfill & 1 \hfill \\
\end{array} } \right]
\]](../latex_cache/faa48ff3c983ec75ba4a7260fa7609dc.png)
and H is actually nothing but [-P I3]. It can be seen that HGTs will always result {0,0,0} in a parity check, meaning that all three parities have passed the test. So, where is the problem?
Noise: Noise is the operator that flips the values of bits randomly with an occuring probability f. Suppose that we have a source signal block of 4 bits length: {s1, s2, s3, s4}. I encode this information with calculating the parities and adding them to the end, thus coming up with a block of 7 bits length and call this block as t (for transmitted):
t=GTs (supposing t and s are given as column vectors. Otherwise, t=sG)
Now I send this packet but on the road to the receiver, the noise changes it and so, the received message, r, is the transmitted message (t) AND the noise (n):
r=t+s
Since I have got the parity information part (which may also have been affected by the noise), I compare the received data’s first 4 values with the parity information stored in the last 3 values. A very practical way of doing this is using 3 intersecting circles and placing them as:
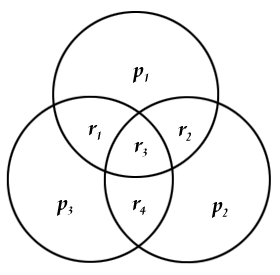
with r1-r4 representing the first values (ie, actual data) received and p1-p3 being the parity information (the last 3 values). So we place the values to their corresponding locations and easily can check if the parity matches to the related values. We can have 8 different situations at this moment. Let’s denote the z=Hr vector as the parity check result. z={0,0,0} if all three parity information agrees with the calculated ones, z={1,0,0} if only p1 is different from the calculated parity of {r1,r2,r3}, z={1,0,1} if p1 AND p3 are different from their corresponding calculated parities and so on. If there is only 1 error (ie, only one "1" and two "0") in the parity check, then it means that, the noise affected only the parity information, not the data encoded (ie, the first 4 values), so the corrupted data can be fixed by simply switching the faulty parity. If there are 2 parity check errors, this time, the value on the intersection of the corresponding parities (ie, r1 for p1&p3, r2 for p1&p2 and r4 for p2&p3,) must be switched. If z={1,1,1} then r3 should be switched.
Let’s introduce some mathematica operations and then tackle with some examples. You can just copy and paste them since there are no additional libraries required:
mGT = {{1,0,0,0},{0,1,0,0},{0,0,1,0},{0,0,0,1},{1,1,1,0},{0,1,1,1},{1,0,1,1}};
mH = {{1,1,1,0,1,0,0},{0,1,1,1,0,1,0},{1,0,1,1,0,0,1}};
(mS = {{1},{1},{1},{0}});
Mod[(mGTS=mGT . mS),2] // MatrixForm
mN ={0,0,0,0,0,0,1};
(mR = Mod[mGTS+mN,2]) // MatrixForm
mZ = Mod[mH . mR,2];
Flatten[mZ]
The first two lines define GT and H and from here, you can check a very important property being:
Mod[mH.mGT,2] // MatrixForm
equal to 0.
We introduce the 4bit data to be transmitted as mS which we had referred as s through out the text. Then we encode the data to be send with the parity info encoded as mGTS (t) add a noise mN (n) to it assuming it is corrupted in the transmission process and the data the other side receives is mR (r) consisting of the data transmitted AND the noise acted on it. mZ is the parity check result (z) (I’ve "Flatten"ed it for a better view). In the operations above, the "Mod" operator is frequently used because of our universe being a mod2 universe (2=0, 3=1, 4=0,… just 0s and 1s actually!).
So, in this example, we had s={1,1,1,0}, and this was encoded as t={1,1,1,0,1,0,0} and on its way to the happy-ending, a noise corrupted it and switched its 3rd parity information from 0 to 1. As a result of this, the recipient got its data as r={1,1,1,0,1,0,1}. But since our recipient is not that dull, a parity check is immediately applied and it was seen that z={0,0,1} meaning that, there is something wrong with the 3rd parity information, and nothing wrong with the information received at all!
Now, let’s apply all the possible noises given that only one value can be switched at a time (ie, only one 1 in the n vector with the remaining all being 0s).
For[i = 1, i <= 7, i++,
mN = {0, 0, 0, 0, 0, 0, 0} ;
mN = ReplacePart[mN, 1, i];
mR = Mod[mGTS + mN, 2];
mZ = Mod[mH . mR, 2];
Print[mN, "\t", Flatten[mZ]];
];
After this, if everything went right, you’ll see the output something like this:
{1,0,0,0,0,0,0} {1,0,1}
{0,1,0,0,0,0,0} {1,1,0}
{0,0,1,0,0,0,0} {1,1,1}
{0,0,0,1,0,0,0} {0,1,1}
{0,0,0,0,1,0,0} {1,0,0}
{0,0,0,0,0,1,0} {0,1,0}
{0,0,0,0,0,0,1} {0,0,1}
So we know exactly what went wrong at are able to correct it… Everything seems so perfect, so there must be a catch…
There is no decoding error as long as there is only 1 corruption per data block!
As the corruption number increases, there is no way of achieving the original data send with precise accuracy. Suppose that we re-send our previous signal s={1,1,1,0} which yields t={1,1,1,0,1,0,0} but this time the noise associated with the signal is n={0,1,0,0,0,0,1} so, the received signal is r={1,0,1,0,1,0,1}. When we apply the partition check, we have z={1,1,1}, which means that, there is a problem with the 3rd value and we deduce that the original message transmitted was t={1,0,0,0,1,0,1} which passes the parity check tests with success alas a wrongly decoded signal!
The probability of block error, pB is the probability that there will at least be one decoded bit that will not match the transmitted bit. A little attention must be paid about this statement. It emphasizes the decoded bit part, not the received bit. So, in our case of (4,7) Hamming Code, there won’t be a block error as long as there is only one corrupted bit in the received bit because we are able to construct the transmitted bits with certainty in that case. Only if we have two or more bits corrupted, we won’t be able to revive the original signal, so, pB scales as O(f2).
References : I have heavily benefitted from David MacKay’s resourceful book Information Theory, Inference, and Learning Algorithms which is available for free for viewing on screen.
|
Mathematica Matrix Examples
November 19, 2007 Posted by Emre S. Tasci
Mathematica Matrix Manipulation Examples
B={Range[5],Range[6,10],Range[11,15],Range[16,20]} ;
TableForm[B]
(* To extract rows 2 & 3 *)
Part[B,{2,3}] // TableForm
(* To extract cols 2 & 4 *)
Part[B, All,{2,4}] // TableForm
(* To extract the intersection of Rows 2&3 with Cols 2&4 *)
Part[B,{2,3} ,{2,4}] // TableForm
(* Selecting the values from the 2. row where B[[4]][[i]] has a specific value like <10 *)
Select[B[[2]],#<10&]
(* Selecting the values from the 2. col where B[[i]][[2]] has a specific value like <10 *)Select[Part[B,All,2],#<10&]
(* Alternative Transpose (//Equivalent to Transpose[matrixIN]//)*)
TransposeEST[matrixIN_]:=Module[
{matrixOUT},
numCols = Dimensions[matrixIN][[2]];
matrixOUT = Array[mo,numCols];
For[i=1,i<=numCols,i++,
� � � matrixOUT[[i]]=Part[matrixIN,All,i];
]
TableForm[matrixOUT];
Return[matrixOUT];
]
(* Swapping two rows *)
({B[[2]],B[[4]]}={B[[4]],B[[2]]}) // TableForm
(*Reading data from a file with a content like this:
0.642864000 0.761961000 1.665420000
5.815150000 3.603020000 1.831920000
6.409050000 7.150810000 0.966674000
5.389080000 4.989350000 6.571080000
6.044070000 4.887170000 7.005700000
6.806280000 2.766540000 4.030720000
6.676540000 0.652834000 5.729050000
1.231490000 5.754580000 0.404114000
9.722660000 7.571420000 1.133980000
8.869320000 7.574570000 4.886290000
1.221750000 8.511380000 6.201370000
2.817450000 0.216682000 6.474590000
5.638430000 7.422500000 7.381840000
8.903770000 4.192770000 0.355182000
7.073810000 1.421990000 1.606240000
7.646660000 1.979770000 3.877830000
8.239190000 1.280060000 6.705840000
4.430740000 2.016050000 5.515660000
9.771000000 2.637290000 8.423900000
8.916410000 4.900040000 2.592560000
*)
m=OpenRead["d:\lol1.txt"];
k= ReadList[m,Number];
Close[m];
(k =Partition[k,3]) // TableForm
(* And you can definitely Plot it too *)
<<Graphics`Graphics3D`
ScatterPlot3D[k,PlotStyle®{{PointSize[0.04],GrayLevel[0.09]}}]



