Some “trivial” derivations
December 4, 2007 Posted by Emre S. Tasci
Information Theory, Inference, and Learning Algorithms by David MacKay, Exercise 22.5:
A random variable x is assumed to have a probability distribution that is a mixture of two Gaussians,
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamiEaiaacYhacqaH8oqBdaWgaaWcbaGaaGymaaqabaGccaGG
% SaGaeqiVd02aaSbaaSqaaiaaikdaaeqaaOGaaiilaiabeo8aZbGaay
% jkaiaawMcaaiabg2da9maadmaabaWaaabCaeaacaWGWbWaaSbaaSqa
% aiaadUgaaeqaaOWaaSaaaeaacaaIXaaabaWaaOaaaeaacaaIYaGaeq
% iWdaNaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaqabaaaaOGaciyzaiaa
% cIhacaGGWbWaaeWaaeaacqGHsisldaWcaaqaamaabmaabaGaamiEai
% abgkHiTiabeY7aTnaaBaaaleaacaWGRbaabeaaaOGaayjkaiaawMca
% amaaCaaaleqabaGaaGOmaaaaaOqaaiaaikdacqaHdpWCdaahaaWcbe
% qaaiaaikdaaaaaaaGccaGLOaGaayzkaaaaleaacaWGRbGaeyypa0Ja
% aGymaaqaaiaaikdaa0GaeyyeIuoaaOGaay5waiaaw2faaaaa!63A5!
\[
P\left( {x|\mu _1 ,\mu _2 ,\sigma } \right) = \left[ {\sum\limits_{k = 1}^2 {p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x - \mu _k } \right)^2 }}
{{2\sigma ^2 }}} \right)} } \right]
\]](../latex_cache/02ffa24cafcda9c52b21f37689acad79.png)
where the two Gaussians are given the labels k = 1 and k = 2; the prior probability of the class label k is {p1 = 1/2, p2 = 1/2}; ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacq
% aH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawUhacaGL9baaaaa!3AFA!
\[
{\left\{ {\mu _k } \right\}}
\]](../latex_cache/63181a36e52687072bbbd54c4488895f.png) are the means of the two Gaussians; and both have standard deviation sigma. For brevity, we denote these parameters by
are the means of the two Gaussians; and both have standard deviation sigma. For brevity, we denote these parameters by
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCiUdiabgg
% Mi6oaacmaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam4Aaaqabaaa
% kiaawUhacaGL9baacaGGSaGaeq4WdmhacaGL7bGaayzFaaaaaa!42AB!
\[
{\mathbf{\theta }} \equiv \left\{ {\left\{ {\mu _k } \right\},\sigma } \right\}
\]](../latex_cache/0872f8d876f08afa90626cfb8bfd6165.png)
A data set consists of N points ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaaca
% WG4bWaaSbaaSqaaiaad6gaaeqaaaGccaGL7bGaayzFaaWaa0baaSqa
% aiaad6gacqGH9aqpcaaIXaaabaGaamOtaaaaaaa!3DF8!
\[
\left\{ {x_n } \right\}_{n = 1}^N
\]](../latex_cache/5960b3e63e93b0eadb7f05b6597dc081.png) which are assumed to be independent samples from the distribution. Let kn denote the unknown class label of the nth point.
which are assumed to be independent samples from the distribution. Let kn denote the unknown class label of the nth point.
Assuming that ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacq
% aH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawUhacaGL9baaaaa!3AFA!
\[
{\left\{ {\mu _k } \right\}}
\]](../latex_cache/63181a36e52687072bbbd54c4488895f.png) and
and ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdmhaaa!37B0!
\[
\sigma
\]](../latex_cache/0bcead44095f85d706d5bd0d3ee69019.png) are known, show that the posterior probability of the class label kn of the nth point can be written as
are known, show that the posterior probability of the class label kn of the nth point can be written as
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb
% WaaeWaaeaadaabcaqaaiaadUgadaWgaaWcbaGaamOBaaqabaGccqGH
% 9aqpcaaIXaaacaGLiWoacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaai
% ilaiaahI7aaiaawIcacaGLPaaacqGH9aqpdaWcaaqaaiaaigdaaeaa
% caaIXaGaey4kaSIaciyzaiaacIhacaGGWbWaamWaaeaacqGHsislda
% qadaqaaiabeM8a3naaBaaaleaacaaIXaaabeaakiaadIhadaWgaaWc
% baGaamOBaaqabaGccqGHRaWkcqaHjpWDdaWgaaWcbaGaaGimaaqaba
% aakiaawIcacaGLPaaaaiaawUfacaGLDbaaaaaabaGaamiuamaabmaa
% baWaaqGaaeaacaWGRbWaaSbaaSqaaiaad6gaaeqaaOGaeyypa0JaaG
% OmaaGaayjcSdGaamiEamaaBaaaleaacaWGUbaabeaakiaacYcacaWH
% 4oaacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaaIXaaabaGaaGymai
% abgUcaRiGacwgacaGG4bGaaiiCamaadmaabaGaey4kaSYaaeWaaeaa
% cqaHjpWDdaWgaaWcbaGaaGymaaqabaGccaWG4bWaaSbaaSqaaiaad6
% gaaeqaaOGaey4kaSIaeqyYdC3aaSbaaSqaaiaaicdaaeqaaaGccaGL
% OaGaayzkaaaacaGLBbGaayzxaaaaaaaaaa!7422!
\[
\begin{gathered}
P\left( {\left. {k_n = 1} \right|x_n ,{\mathbf{\theta }}} \right) = \frac{1}
{{1 + \exp \left[ { - \left( {\omega _1 x_n + \omega _0 } \right)} \right]}} \hfill \\
P\left( {\left. {k_n = 2} \right|x_n ,{\mathbf{\theta }}} \right) = \frac{1}
{{1 + \exp \left[ { + \left( {\omega _1 x_n + \omega _0 } \right)} \right]}} \hfill \\
\end{gathered}
\]](../latex_cache/f1256d14a59790f5d35c2bedc4a49bbc.png)
and give expressions for ![Formula: \[\omega _1 \]](../latex_cache/9b85d537fe39f505e5182913d97fdfb8.png) and
and ![Formula: \[\omega _0 \]](../latex_cache/dfa670f67ce3c9849cc5c143a295efac.png) .
.
Derivation:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaWaaqGaaeaacaWGRbWaaSbaaSqaaiaad6gaaeqaaOGaeyypa0Ja
% aGymaaGaayjcSdGaamiEamaaBaaaleaacaWGUbaabeaakiaacYcaca
% WH4oaacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaWGqbWaaeWaaeaa
% caWG4bWaaSbaaSqaaiaad6gaaeqaaOWaaqqaaeaacaWGRbWaaSbaaS
% qaaiaad6gaaeqaaOGaeyypa0JaaGymaiaacYcacaWH4oaacaGLhWoa
% aiaawIcacaGLPaaacaWGqbWaaeWaaeaacaWGRbWaaSbaaSqaaiaad6
% gaaeqaaOGaeyypa0JaaGymaaGaayjkaiaawMcaaaqaaiaadcfadaqa
% daqaaiaadIhadaWgaaWcbaGaamOBaaqabaaakiaawIcacaGLPaaaaa
% aaaa!598D!
\[
P\left( {\left. {k_n = 1} \right|x_n ,{\mathbf{\theta }}} \right) = \frac{{P\left( {x_n \left| {k_n = 1,{\mathbf{\theta }}} \right.} \right)P\left( {k_n = 1} \right)}}
{{P\left( {x_n } \right)}}
\]](../latex_cache/a715c20187b7d1333ddd7eac5d275abb.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamiEamaaBaaaleaacaWGUbaabeaakmaaeeaabaGaam4Aamaa
% BaaaleaacaWGUbaabeaakiabg2da9iaaigdacaGGSaGaaCiUdaGaay
% 5bSdaacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaaIXaaabaWaaOaa
% aeaacaaIYaGaeqiWdaNaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaqaba
% aaaOGaciyzaiaacIhacaGGWbWaaeWaaeaacqGHsisldaWcaaqaamaa
% bmaabaGaamiEamaaBaaaleaacaWGUbaabeaakiabgkHiTiabeY7aTn
% aaBaaaleaacaaIXaaabeaaaOGaayjkaiaawMcaamaaCaaaleqabaGa
% aGOmaaaaaOqaaiaaikdacqaHdpWCdaahaaWcbeqaaiaaikdaaaaaaa
% GccaGLOaGaayzkaaaaaa!59EC!
\[
P\left( {x_n \left| {k_n = 1,{\mathbf{\theta }}} \right.} \right) = \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x_n - \mu _1 } \right)^2 }}
{{2\sigma ^2 }}} \right)
\]](../latex_cache/fad7cf1dcafb714f7a176d734a527a09.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamiEamaaBaaaleaacaWGUbaabeaaaOGaayjkaiaawMcaaiab
% g2da9maaqahabaGaamiuamaabmaabaWaaqGaaeaacaWG4bWaaSbaaS
% qaaiaad6gaaeqaaaGccaGLiWoacaWGRbWaaSbaaSqaaiaad6gaaeqa
% aOGaeyypa0JaamyAaiaacYcacaWH4oaacaGLOaGaayzkaaGaamiuam
% aabmaabaGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaadMga
% aiaawIcacaGLPaaaaSqaaiaadMgacqGH9aqpcaaIXaaabaGaaGOmaa
% qdcqGHris5aaaa!53AA!
\[
P\left( {x_n } \right) = \sum\limits_{i = 1}^2 {P\left( {\left. {x_n } \right|k_n = i,{\mathbf{\theta }}} \right)P\left( {k_n = i} \right)}
\]](../latex_cache/4552f718d3d4a5d314db5eec6e935fe6.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb
% WaaeWaaeaadaabcaqaaiaadUgadaWgaaWcbaGaamOBaaqabaGccqGH
% 9aqpcaaIXaaacaGLiWoacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaai
% ilaiaahI7aaiaawIcacaGLPaaacqGH9aqpdaWcaaqaamaalaaabaGa
% aGymaaqaamaakaaabaGaaGOmaiabec8aWjabeo8aZnaaCaaaleqaba
% GaaGOmaaaaaeqaaaaakiGacwgacaGG4bGaaiiCamaabmaabaGaeyOe
% I0YaaSaaaeaadaqadaqaaiaadIhadaWgaaWcbaGaamOBaaqabaGccq
% GHsislcqaH8oqBdaWgaaWcbaGaaGymaaqabaaakiaawIcacaGLPaaa
% daahaaWcbeqaaiaaikdaaaaakeaacaaIYaGaeq4Wdm3aaWbaaSqabe
% aacaaIYaaaaaaaaOGaayjkaiaawMcaaiaadcfadaqadaqaaiaadUga
% daWgaaWcbaGaamOBaaqabaGccqGH9aqpcaaIXaaacaGLOaGaayzkaa
% aabaWaaSaaaeaacaaIXaaabaWaaOaaaeaacaaIYaGaeqiWdaNaeq4W
% dm3aaWbaaSqabeaacaaIYaaaaaqabaaaaOGaciyzaiaacIhacaGGWb
% WaaeWaaeaacqGHsisldaWcaaqaamaabmaabaGaamiEamaaBaaaleaa
% caWGUbaabeaakiabgkHiTiabeY7aTnaaBaaaleaacaaIXaaabeaaaO
% GaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaOqaaiaaikdacqaH
% dpWCdaahaaWcbeqaaiaaikdaaaaaaaGccaGLOaGaayzkaaGaamiuam
% aabmaabaGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaaigda
% aiaawIcacaGLPaaacqGHRaWkdaWcaaqaaiaaigdaaeaadaGcaaqaai
% aaikdacqaHapaCcqaHdpWCdaahaaWcbeqaaiaaikdaaaaabeaaaaGc
% ciGGLbGaaiiEaiaacchadaqadaqaaiabgkHiTmaalaaabaWaaeWaae
% aacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaeyOeI0IaeqiVd02aaSba
% aSqaaiaaikdaaeqaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaIYa
% aaaaGcbaGaaGOmaiabeo8aZnaaCaaaleqabaGaaGOmaaaaaaaakiaa
% wIcacaGLPaaacaWGqbWaaeWaaeaacaWGRbWaaSbaaSqaaiaad6gaae
% qaaOGaeyypa0JaaGOmaaGaayjkaiaawMcaaaaaaeaacqGH9aqpdaWc
% aaqaaiaaigdaaeaacaaIXaGaey4kaSIaciyzaiaacIhacaGGWbWaae
% WaaeaacqGHsisldaWcaaqaamaabmaabaGaamiEamaaBaaaleaacaWG
% UbaabeaakiabgkHiTiabeY7aTnaaBaaaleaacaaIYaaabeaaaOGaay
% jkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaOqaaiaaikdacqaHdpWC
% daahaaWcbeqaaiaaikdaaaaaaOGaey4kaSYaaSaaaeaadaqadaqaai
% aadIhadaWgaaWcbaGaamOBaaqabaGccqGHsislcqaH8oqBdaWgaaWc
% baGaaGymaaqabaaakiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaa
% aakeaacaaIYaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaaaOGaayjk
% aiaawMcaamaabmaabaWaaSaaaeaacaaIXaGaeyOeI0Iaamiuamaabm
% aabaGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaaigdaaiaa
% wIcacaGLPaaaaeaacaWGqbWaaeWaaeaacaWGRbWaaSbaaSqaaiaad6
% gaaeqaaOGaeyypa0JaaGymaaGaayjkaiaawMcaaaaaaiaawIcacaGL
% Paaaaaaaaaa!CC7A!
\[
\begin{gathered}
P\left( {\left. {k_n = 1} \right|x_n ,{\mathbf{\theta }}} \right) = \frac{{\frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x_n - \mu _1 } \right)^2 }}
{{2\sigma ^2 }}} \right)P\left( {k_n = 1} \right)}}
{{\frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x_n - \mu _1 } \right)^2 }}
{{2\sigma ^2 }}} \right)P\left( {k_n = 1} \right) + \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x_n - \mu _2 } \right)^2 }}
{{2\sigma ^2 }}} \right)P\left( {k_n = 2} \right)}} \hfill \\
= \frac{1}
{{1 + \exp \left( { - \frac{{\left( {x_n - \mu _2 } \right)^2 }}
{{2\sigma ^2 }} + \frac{{\left( {x_n - \mu _1 } \right)^2 }}
{{2\sigma ^2 }}} \right)\left( {\frac{{1 - P\left( {k_n = 1} \right)}}
{{P\left( {k_n = 1} \right)}}} \right)}} \hfill \\
\end{gathered}
\]](../latex_cache/1e6fdf2c5d24e2be5c59df57c14121ec.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS
% aaaeaacaaIXaaabaGaaGymaiabgUcaRiGacwgacaGG4bGaaiiCamaa
% dmaabaGaeyOeI0YaaeWaaeaadaqadaqaamaalaaabaWaaeWaaeaacq
% aH8oqBdaWgaaWcbaGaaGymaaqabaGccqGHsislcqaH8oqBdaWgaaWc
% baGaaGOmaaqabaaakiaawIcacaGLPaaaaeaacqaHdpWCdaahaaWcbe
% qaaiaaikdaaaaaaaGccaGLOaGaayzkaaGaamiEamaaBaaaleaacaWG
% UbaabeaakiabgUcaRmaabmaabaWaaSaaaeaadaqadaqaaiabeY7aTn
% aaBaaaleaacaaIYaaabeaakmaaCaaaleqabaGaaGOmaaaakiabgkHi
% TiabeY7aTnaaBaaaleaacaaIXaaabeaakmaaCaaaleqabaGaaGOmaa
% aaaOGaayjkaiaawMcaaaqaaiaaikdacqaHdpWCdaahaaWcbeqaaiaa
% ikdaaaaaaaGccaGLOaGaayzkaaaacaGLOaGaayzkaaaacaGLBbGaay
% zxaaaaaaaa!5E70!
\[
= \frac{1}
{{1 + \exp \left[ { - \left( {\left( {\frac{{\left( {\mu _1 - \mu _2 } \right)}}
{{\sigma ^2 }}} \right)x_n + \left( {\frac{{\left( {\mu _2 ^2 - \mu _1 ^2 } \right)}}
{{2\sigma ^2 }}} \right)} \right)} \right]}}
\]](../latex_cache/2cb3dc1005d19db77232acac5cfde110.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS
% aaaeaacaaIXaaabaGaaGymaiabgUcaRiGacwgacaGG4bGaaiiCamaa
% dmaabaGaeyOeI0YaaeWaaeaacqaHjpWDdaWgaaWcbaGaaGymaaqaba
% GccaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaey4kaSIaeqyYdC3aaSba
% aSqaaiaaicdaaeqaaaGccaGLOaGaayzkaaaacaGLBbGaayzxaaaaaa
% aa!4921!
\[
= \frac{1}
{{1 + \exp \left[ { - \left( {\omega _1 x_n + \omega _0 } \right)} \right]}}
\]](../latex_cache/fad0a283da2a75ecc80ae95039e225d9.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyYdC3aaS
% baaSqaaiaaigdaaeqaaOGaeyyyIO7aaSaaaeaadaqadaqaaiabeY7a
% TnaaBaaaleaacaaIXaaabeaakiabgkHiTiabeY7aTnaaBaaaleaaca
% aIYaaabeaaaOGaayjkaiaawMcaaaqaaiabeo8aZnaaCaaaleqabaGa
% aGOmaaaaaaGccaGG7aGaaCzcaiabeM8a3naaBaaaleaacaaIWaaabe
% aakiabggMi6oaalaaabaWaaeWaaeaacqaH8oqBdaWgaaWcbaGaaGOm
% aaqabaGcdaahaaWcbeqaaiaaikdaaaGccqGHsislcqaH8oqBdaWgaa
% WcbaGaaGymaaqabaGcdaahaaWcbeqaaiaaikdaaaaakiaawIcacaGL
% PaaaaeaacaaIYaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaaaaa!5809!
\[
\omega _1 \equiv \frac{{\left( {\mu _1 - \mu _2 } \right)}}
{{\sigma ^2 }}; & \omega _0 \equiv \frac{{\left( {\mu _2 ^2 - \mu _1 ^2 } \right)}}
{{2\sigma ^2 }}
\]](../latex_cache/ecb970e7b19db2f916b89d7f4f9ff62f.png)
Assume now that the means ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacq
% aH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawUhacaGL9baaaaa!3AFA!
\[
{\left\{ {\mu _k } \right\}}
\]](../latex_cache/63181a36e52687072bbbd54c4488895f.png) are not known, and that we wish to infer them from the data
are not known, and that we wish to infer them from the data ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaaca
% WG4bWaaSbaaSqaaiaad6gaaeqaaaGccaGL7bGaayzFaaWaa0baaSqa
% aiaad6gacqGH9aqpcaaIXaaabaGaamOtaaaaaaa!3DF8!
\[
\left\{ {x_n } \right\}_{n = 1}^N
\]](../latex_cache/5960b3e63e93b0eadb7f05b6597dc081.png) . (The standard deviation
. (The standard deviation ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdmhaaa!37B0!
\[
\sigma
\]](../latex_cache/0bcead44095f85d706d5bd0d3ee69019.png) is known.) In the remainder of this question we will derive an iterative algorithm for finding values for
is known.) In the remainder of this question we will derive an iterative algorithm for finding values for ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacq
% aH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawUhacaGL9baaaaa!3AFA!
\[
{\left\{ {\mu _k } \right\}}
\]](../latex_cache/63181a36e52687072bbbd54c4488895f.png) that maximize the likelihood,
that maximize the likelihood,
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaWaaiWaaeaacaWG4bWaaSbaaSqaaiaad6gaaeqaaaGccaGL7bGa
% ayzFaaWaa0baaSqaaiaad6gacqGH9aqpcaaIXaaabaGaamOtaaaakm
% aaeeaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam4Aaaqabaaakiaa
% wUhacaGL9baacaGGSaGaeq4WdmhacaGLhWoaaiaawIcacaGLPaaacq
% GH9aqpdaqeqbqaaiaadcfadaqadaqaaiaadIhadaWgaaWcbaGaamOB
% aaqabaGcdaabbaqaamaacmaabaGaeqiVd02aaSbaaSqaaiaadUgaae
% qaaaGccaGL7bGaayzFaaGaaiilaiabeo8aZbGaay5bSdaacaGLOaGa
% ayzkaaaaleaacaWGUbaabeqdcqGHpis1aOGaaiOlaaaa!5BD3!
\[
P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \prod\limits_n {P\left( {x_n \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right)} .
\]](../latex_cache/e8f09972b3500b374a1e5b0fd19ae615.png)
Let L denote the natural log of the likelihood. Show that the derivative of the log likelihood with respect to ![Formula: \[{\mu _k }\]](../latex_cache/8e114e04047dfd2df6cd90fecc90cc9d.png) is given by
is given by
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
% GHciITaeaacqGHciITcqaH8oqBdaWgaaWcbaGaam4AaaqabaaaaOGa
% amitaiabg2da9maaqafabaGaamiCamaaBaaaleaacaWGRbGaaiiFai
% aad6gaaeqaaOWaaSaaaeaadaqadaqaaiaadIhadaWgaaWcbaGaamOB
% aaqabaGccqGHsislcqaH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawI
% cacaGLPaaaaeaacqaHdpWCdaahaaWcbeqaaiaaikdaaaaaaOGaaiil
% aaWcbaGaamOBaaqab0GaeyyeIuoaaaa!4F8E!
\[
\frac{\partial }
{{\partial \mu _k }}L = \sum\limits_n {p_{k|n} \frac{{\left( {x_n - \mu _k } \right)}}
{{\sigma ^2 }},}
\]](../latex_cache/968180dae9f9ec36821998cd8cc198f2.png)
where ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
% aaleaacaWGRbGaaiiFaiaad6gaaeqaaOGaeyyyIORaamiuamaabmaa
% baGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaadUgadaabba
% qaaiaadIhadaWgaaWcbaGaamOBaaqabaGccaGGSaGaaCiUdaGaay5b
% SdaacaGLOaGaayzkaaaaaa!47DF!
\[
p_{k|n} \equiv P\left( {k_n = k\left| {x_n ,{\mathbf{\theta }}} \right.} \right)
\]](../latex_cache/1b5e0ed28e9818454709a25da45ef545.png) appeared above.
appeared above.
Derivation:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
% GHciITaeaacqGHciITcqaH8oqBdaWgaaWcbaGaam4AaaqabaaaaOGa
% ciiBaiaac6gacaWGqbWaaeWaaeaadaGadaqaaiaadIhadaWgaaWcba
% GaamOBaaqabaaakiaawUhacaGL9baadaqhaaWcbaGaamOBaiabg2da
% 9iaaigdaaeaacaWGobaaaOWaaqqaaeaadaGadaqaaiabeY7aTnaaBa
% aaleaacaWGRbaabeaaaOGaay5Eaiaaw2haaiaacYcacqaHdpWCaiaa
% wEa7aaGaayjkaiaawMcaaiabg2da9maalaaabaGaeyOaIylabaGaey
% OaIyRaeqiVd02aaSbaaSqaaiaadUgaaeqaaaaakmaaqafabaGaciiB
% aiaac6gacaWGqbWaaeWaaeaacaWG4bWaaSbaaSqaaiaad6gaaeqaaO
% WaaqqaaeaadaGadaqaaiabeY7aTnaaBaaaleaacaWGRbaabeaaaOGa
% ay5Eaiaaw2haaiaacYcacqaHdpWCaiaawEa7aaGaayjkaiaawMcaaa
% WcbaGaamOBaaqab0GaeyyeIuoaaaa!6A60!
\[
\frac{\partial }
{{\partial \mu _k }}\ln P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \frac{\partial }
{{\partial \mu _k }}\sum\limits_n {\ln P\left( {x_n \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right)}
\]](../latex_cache/d4fff688e4cb4a830395b148a0388ad0.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS
% aaaeaacqGHciITaeaacqGHciITcqaH8oqBdaWgaaWcbaGaam4Aaaqa
% baaaaOWaaabuaeaaciGGSbGaaiOBamaadmaabaWaaabuaeaacaWGWb
% WaaSbaaSqaaiaadUgaaeqaaOWaaSaaaeaacaaIXaaabaWaaOaaaeaa
% caaIYaGaeqiWdaNaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaqabaaaaO
% GaciyzaiaacIhacaGGWbWaamWaaeaacqGHsisldaWcaaqaamaabmaa
% baGaeqiVd02aaSbaaSqaaiaadUgaaeqaaOGaeyOeI0IaamiEamaaBa
% aaleaacaWGUbaabeaaaOGaayjkaiaawMcaamaaCaaaleqabaGaaGOm
% aaaaaOqaaiaaikdacqaHdpWCdaahaaWcbeqaaiaaikdaaaaaaaGcca
% GLBbGaayzxaaaaleaacaWGRbaabeqdcqGHris5aaGccaGLBbGaayzx
% aaaaleaacaWGUbaabeqdcqGHris5aaaa!6080!
\[
= \frac{\partial }
{{\partial \mu _k }}\sum\limits_n {\ln \left[ {\sum\limits_k {p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right]} } \right]}
\]](../latex_cache/86e7b4035c45e740407f4e2862f3fcca.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Zaaa
% buaeaadaWadaqaamaalaaabaGaamiCamaaBaaaleaacaWGRbaabeaa
% kmaalaaabaGaaGymaaqaamaakaaabaGaaGOmaiabec8aWjabeo8aZn
% aaCaaaleqabaGaaGOmaaaaaeqaaaaakmaalaaabaWaaeWaaeaacaWG
% 4bWaaSbaaSqaaiaad6gaaeqaaOGaeyOeI0IaeqiVd02aaSbaaSqaai
% aadUgaaeqaaaGccaGLOaGaayzkaaaabaGaeq4Wdm3aaWbaaSqabeaa
% caaIYaaaaaaakiGacwgacaGG4bGaaiiCamaadmaabaGaeyOeI0YaaS
% aaaeaadaqadaqaaiabeY7aTnaaBaaaleaacaWGRbaabeaakiabgkHi
% TiaadIhadaWgaaWcbaGaamOBaaqabaaakiaawIcacaGLPaaadaahaa
% WcbeqaaiaaikdaaaaakeaacaaIYaGaeq4Wdm3aaWbaaSqabeaacaaI
% YaaaaaaaaOGaay5waiaaw2faaaqaamaaqafabaGaamiCamaaBaaale
% aacaWGRbaabeaakmaalaaabaGaaGymaaqaamaakaaabaGaaGOmaiab
% ec8aWjabeo8aZnaaCaaaleqabaGaaGOmaaaaaeqaaaaakiGacwgaca
% GG4bGaaiiCamaadmaabaGaeyOeI0YaaSaaaeaadaqadaqaaiabeY7a
% TnaaBaaaleaacaWGRbaabeaakiabgkHiTiaadIhadaWgaaWcbaGaam
% OBaaqabaaakiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaakeaa
% caaIYaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaaaOGaay5waiaaw2
% faaaWcbaGaam4Aaaqab0GaeyyeIuoaaaaakiaawUfacaGLDbaaaSqa
% aiaad6gaaeqaniabggHiLdaaaa!7CFE!
\[
= \sum\limits_n {\left[ {\frac{{p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\frac{{\left( {x_n - \mu _k } \right)}}
{{\sigma ^2 }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right]}}
{{\sum\limits_k {p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right]} }}} \right]}
\]](../latex_cache/36d5d46d163b2f0805d07742b2476015.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaabuaeaaca
% WGWbWaaSbaaSqaaiaadUgaaeqaaOWaaSaaaeaacaaIXaaabaWaaOaa
% aeaacaaIYaGaeqiWdaNaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaqaba
% aaaOGaciyzaiaacIhacaGGWbWaamWaaeaacqGHsisldaWcaaqaamaa
% bmaabaGaeqiVd02aaSbaaSqaaiaadUgaaeqaaOGaeyOeI0IaamiEam
% aaBaaaleaacaWGUbaabeaaaOGaayjkaiaawMcaamaaCaaaleqabaGa
% aGOmaaaaaOqaaiaaikdacqaHdpWCdaahaaWcbeqaaiaaikdaaaaaaa
% GccaGLBbGaayzxaaaaleaacaWGRbaabeqdcqGHris5aOGaeyypa0Za
% aabuaeaacaWGqbWaaeWaaeaadaabcaqaaiaadIhadaWgaaWcbaGaam
% OBaaqabaaakiaawIa7aiaadUgadaWgaaWcbaGaamOBaaqabaGccqGH
% 9aqpcaWGPbGaaiilaiaahI7aaiaawIcacaGLPaaacaWGqbWaaeWaae
% aacaWGRbWaaSbaaSqaaiaad6gaaeqaaOGaeyypa0JaamyAaaGaayjk
% aiaawMcaaaWcbaGaamyAaaqab0GaeyyeIuoaaaa!6973!
\[
\sum\limits_k {p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right]} = \sum\limits_i {P\left( {\left. {x_n } \right|k_n = i,{\mathbf{\theta }}} \right)P\left( {k_n = i} \right)}
\]](../latex_cache/ac64de78a66933a927e697ce3399accb.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
% aaleaacaWGRbaabeaakmaalaaabaGaaGymaaqaamaakaaabaGaaGOm
% aiabec8aWjabeo8aZnaaCaaaleqabaGaaGOmaaaaaeqaaaaakiGacw
% gacaGG4bGaaiiCamaadmaabaGaeyOeI0YaaSaaaeaadaqadaqaaiab
% eY7aTnaaBaaaleaacaWGRbaabeaakiabgkHiTiaadIhadaWgaaWcba
% GaamOBaaqabaaakiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaa
% keaacaaIYaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaaaOGaay5wai
% aaw2faaiabg2da9iaadcfadaqadaqaaiaadUgadaWgaaWcbaGaamOB
% aaqabaGccqGH9aqpcaWGRbaacaGLOaGaayzkaaGaamiuamaabmaaba
% GaamiEamaaBaaaleaacaWGUbaabeaakmaaeeaabaGaam4AamaaBaaa
% leaacaWGUbaabeaakiabg2da9iaadUgacaGGSaGaaCiUdaGaay5bSd
% aacaGLOaGaayzkaaaaaa!6347!
\[
p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right] = P\left( {k_n = k} \right)P\left( {x_n \left| {k_n = k,{\mathbf{\theta }}} \right.} \right)
\]](../latex_cache/e7fad6f8f95484fb7540dd2f4a2fc8fc.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H49aaS
% aaaeaacqGHciITaeaacqGHciITcqaH8oqBdaWgaaWcbaGaam4Aaaqa
% baaaaOGaciiBaiaac6gacaWGqbWaaeWaaeaadaGadaqaaiaadIhada
% WgaaWcbaGaamOBaaqabaaakiaawUhacaGL9baadaqhaaWcbaGaamOB
% aiabg2da9iaaigdaaeaacaWGobaaaOWaaqqaaeaadaGadaqaaiabeY
% 7aTnaaBaaaleaacaWGRbaabeaaaOGaay5Eaiaaw2haaiaacYcacqaH
% dpWCaiaawEa7aaGaayjkaiaawMcaaiabg2da9maaqafabaWaaSaaae
% aacaWGqbWaaeWaaeaacaWGRbWaaSbaaSqaaiaad6gaaeqaaOGaeyyp
% a0Jaam4AaaGaayjkaiaawMcaaiaadcfadaqadaqaaiaadIhadaWgaa
% WcbaGaamOBaaqabaGcdaabbaqaaiaadUgadaWgaaWcbaGaamOBaaqa
% baGccqGH9aqpcaWGRbGaaiilaiaahI7aaiaawEa7aaGaayjkaiaawM
% caaaqaamaaqafabaGaamiuamaabmaabaWaaqGaaeaacaWG4bWaaSba
% aSqaaiaad6gaaeqaaaGccaGLiWoacaWGRbWaaSbaaSqaaiaad6gaae
% qaaOGaeyypa0JaamyAaiaacYcacaWH4oaacaGLOaGaayzkaaGaamiu
% amaabmaabaGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaadM
% gaaiaawIcacaGLPaaaaSqaaiaadMgaaeqaniabggHiLdaaaaWcbaGa
% amOBaaqab0GaeyyeIuoakmaalaaabaWaaeWaaeaacaWG4bWaaSbaaS
% qaaiaad6gaaeqaaOGaeyOeI0IaeqiVd02aaSbaaSqaaiaadUgaaeqa
% aaGccaGLOaGaayzkaaaabaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaa
% aaaaa!89F6!
\[
\Rightarrow \frac{\partial }
{{\partial \mu _k }}\ln P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \sum\limits_n {\frac{{P\left( {k_n = k} \right)P\left( {x_n \left| {k_n = k,{\mathbf{\theta }}} \right.} \right)}}
{{\sum\limits_i {P\left( {\left. {x_n } \right|k_n = i,{\mathbf{\theta }}} \right)P\left( {k_n = i} \right)} }}} \frac{{\left( {x_n - \mu _k } \right)}}
{{\sigma ^2 }}
\]](../latex_cache/2c3b479a4f50f6a32f51e3e0e2c7c833.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Zaaa
% buaeaacaWGWbWaaSbaaSqaaiaadUgacaGG8bGaamOBaaqabaaabaGa
% amOBaaqab0GaeyyeIuoakmaalaaabaWaaeWaaeaacaWG4bWaaSbaaS
% qaaiaad6gaaeqaaOGaeyOeI0IaeqiVd02aaSbaaSqaaiaadUgaaeqa
% aaGccaGLOaGaayzkaaaabaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaa
% aaaaa!4840!
\[
= \sum\limits_n {p_{k|n} } \frac{{\left( {x_n - \mu _k } \right)}}
{{\sigma ^2 }}
\]](../latex_cache/c8011d7a11739ee0738f1c36b33e36ea.png)
Assuming that ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdmhaaa!37B0!
\[
\sigma
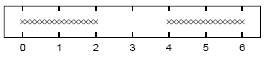
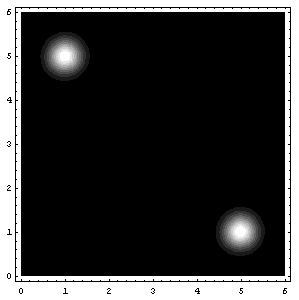
\]](../latex_cache/0bcead44095f85d706d5bd0d3ee69019.png) =1, sketch a contour plot of the likelihood function as a function of mu1 and mu2 for the data set shown above. The data set consists of 32 points. Describe the peaks in your sketch and indicate their widths.
=1, sketch a contour plot of the likelihood function as a function of mu1 and mu2 for the data set shown above. The data set consists of 32 points. Describe the peaks in your sketch and indicate their widths.
Solution:
We will be trying to plot the function
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaWaaiWaaeaacaWG4bWaaSbaaSqaaiaad6gaaeqaaaGccaGL7bGa
% ayzFaaWaa0baaSqaaiaad6gacqGH9aqpcaaIXaaabaGaamOtaaaakm
% aaeeaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam4Aaaqabaaakiaa
% wUhacaGL9baacaGGSaGaeq4WdmNaeyypa0JaaGymaaGaay5bSdaaca
% GLOaGaayzkaaaaaa!4B35!
\[
P\left( {\left\{ {x_n } \right\}_{n = 1}^32 \left| {\left\{ {\mu _k } \right\},\sigma = 1} \right.} \right)
\]](../latex_cache/71b40c661f5c9db63270e0e74a946f2e.png)
if we designate the function
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca
% aIXaaabaWaaOaaaeaacaaIYaGaeqiWdahaleqaaaaakiGacwgacaGG
% 4bGaaiiCamaabmaabaGaeyOeI0YaaSaaaeaadaqadaqaaiaadIhacq
% GHsislcqaH8oqBaiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaa
% keaacaaIYaaaaaGaayjkaiaawMcaaaaa!458F!
\[
{\frac{1}
{{\sqrt {2\pi } }}\exp \left( { - \frac{{\left( {x - \mu } \right)^2 }}
{2}} \right)}
\]](../latex_cache/2ad62d34e3684874733b4cb33953d5d3.png)
as p[x,mu] (remember that ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdmhaaa!37B0!
\[
\sigma
\]](../latex_cache/0bcead44095f85d706d5bd0d3ee69019.png) =1 and
=1 and ![Formula: \[\frac{1}{{\sqrt {2\pi } }} = {\text{0}}{\text{.3989422804014327}}\]](../latex_cache/3007395e2c673cf6173195f8f616e34e.png) ),
),
![Formula: % MathType!MTEF!2!1!+-<br />
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb<br />
% WaaeWaaeaacaWG4bGaaiiFamaacmaabaGaeqiVd0gacaGL7bGaayzF<br />
% aaGaaiilaiabeo8aZbGaayjkaiaawMcaaiabg2da9maadmaabaWaaa<br />
% bCaeaadaqadaqaaiaadchadaWgaaWcbaGaam4AaaqabaGccqGH9aqp<br />
% caGGUaGaaGynaaGaayjkaiaawMcaamaalaaabaGaaGymaaqaamaaka<br />
% aabaGaaGOmaiabec8aWnaabmaabaGaeq4Wdm3aaWbaaSqabeaacaaI<br />
% YaaaaOGaeyypa0JaaGymamaaCaaaleqabaGaaGOmaaaaaOGaayjkai<br />
% aawMcaaaWcbeaaaaGcciGGLbGaaiiEaiaacchadaqadaqaaiabgkHi<br />
% TmaalaaabaWaaeWaaeaacaWG4bGaeyOeI0IaeqiVd02aaSbaaSqaai<br />
% aadUgaaeqaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaaGc<br />
% baGaaGOmaiabeo8aZnaaCaaaleqabaGaaGOmaaaaaaaakiaawIcaca<br />
% GLPaaaaSqaaiaadUgacqGH9aqpcaaIXaaabaGaaGOmaaqdcqGHris5<br />
% aaGccaGLBbGaayzxaaaabaGaeyypa0JaaiOlaiaaiwdadaqadaqaai<br />
% aahchadaWadaqaaiaadIhacaGGSaGaamyBaiaadwhacaaIXaaacaGL<br />
% BbGaayzxaaGaey4kaSIaaCiCamaadmaabaGaamiEaiaacYcacaWGTb<br />
% GaamyDaiaaikdaaiaawUfacaGLDbaaaiaawIcacaGLPaaacqGHHjIU<br />
% caWHWbGaaCiCamaadmaabaGaamiEaiaacYcacaWGTbGaamyDaiaaig<br />
% dacaGGSaGaamyBaiaadwhacaaIYaaacaGLBbGaayzxaaaaaaa!8AA0!<br />
\[<br />
\begin{gathered}<br />
P\left( {x|\left\{ \mu \right\},\sigma } \right) = \left[ {\sum\limits_{k = 1}^2 {\left( {p_k = .5} \right)\frac{1}<br />
{{\sqrt {2\pi \left( {\sigma ^2 = 1^2 } \right)} }}\exp \left( { - \frac{{\left( {x - \mu _k } \right)^2 }}<br />
{{2\sigma ^2 }}} \right)} } \right] \hfill \\<br />
= .5\left( {{\mathbf{p}}\left[ {x,mu1} \right] + {\mathbf{p}}\left[ {x,mu2} \right]} \right) \equiv {\mathbf{pp}}\left[ {x,mu1,mu2} \right] \hfill \\ <br />
\end{gathered} <br />
\]](../latex_cache/d8547ac7bb53e78258a1e9e9b6404ee4.png)
![Formula: % MathType!MTEF!2!1!+-<br />
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb<br />
% WaaeWaaeaadaGadaqaaiaadIhadaWgaaWcbaGaamOBaaqabaaakiaa<br />
% wUhacaGL9baadaqhaaWcbaGaamOBaiabg2da9iaaigdaaeaacaWGob<br />
% aaaOWaaqqaaeaadaGadaqaaiabeY7aTnaaBaaaleaacaWGRbaabeaa<br />
% aOGaay5Eaiaaw2haaiaacYcacqaHdpWCaiaawEa7aaGaayjkaiaawM<br />
% caaiabg2da9maarafabaGaamiuamaabmaabaGaamiEamaaBaaaleaa<br />
% caWGUbaabeaakmaaeeaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam<br />
% 4AaaqabaaakiaawUhacaGL9baacaGGSaGaeq4WdmhacaGLhWoaaiaa<br />
% wIcacaGLPaaaaSqaaiaad6gaaeqaniabg+GivdaakeaacqGH9aqpda<br />
% qeqbqaaiaahchacaWHWbWaamWaaeaacaWG4bGaaiilaiaad2gacaWG<br />
% 1bGaaGymaiaacYcacaWGTbGaamyDaiaaikdaaiaawUfacaGLDbaaaS<br />
% qaaiaad6gaaeqaniabg+GivdGccqGHHjIUcaWHWbGaaCiCaiaahcha<br />
% daWadaqaaiaadIhacaGGSaGaamyBaiaadwhacaaIXaGaaiilaiaad2<br />
% gacaWG1bGaaGOmaaGaay5waiaaw2faaaaaaa!791F!<br />
\[<br />
\begin{gathered}<br />
P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \prod\limits_n {P\left( {x_n \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right)} \hfill \\<br />
= \prod\limits_n {{\mathbf{pp}}\left[ {x,mu1,mu2} \right]} \equiv {\mathbf{ppp}}\left[ {x,mu1,mu2} \right] \hfill \\ <br />
\end{gathered} <br />
\]](../latex_cache/45d43b605033a4aa279f5db4b6c5f8cb.png)
then we have:
![Formula: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb<br />% WaaeWaaeaadaGadaqaaiaadIhadaWgaaWcbaGaamOBaaqabaaakiaa<br />% wUhacaGL9baadaqhaaWcbaGaamOBaiabg2da9iaaigdaaeaacaWGob<br />% aaaOWaaqqaaeaadaGadaqaaiabeY7aTnaaBaaaleaacaWGRbaabeaa<br />% aOGaay5Eaiaaw2haaiaacYcacqaHdpWCaiaawEa7aaGaayjkaiaawM<br />% caaiabg2da9maarafabaGaamiuamaabmaabaGaamiEamaaBaaaleaa<br />% caWGUbaabeaakmaaeeaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam<br />% 4AaaqabaaakiaawUhacaGL9baacaGGSaGaeq4WdmhacaGLhWoaaiaa<br />% wIcacaGLPaaaaSqaaiaad6gaaeqaniabg+GivdaakeaacqGH9aqpda<br />% qeqbqaaiaahchacaWHWbWaamWaaeaacaWG4bGaaiilaiaad2gacaWG<br />% 1bGaaGymaiaacYcacaWGTbGaamyDaiaaikdaaiaawUfacaGLDbaaaS<br />% qaaiaad6gaaeqaniabg+GivdGccqGHHjIUcaWHWbGaaCiCaiaahcha<br />% daWadaqaaiaadIhacaGGSaGaamyBaiaadwhacaaIXaGaaiilaiaad2<br />% gacaWG1bGaaGOmaaGaay5waiaaw2faaaaaaa!791F!<br />\[<br />\begin{gathered}<br /> P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \prod\limits_n {P\left( {x_n \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right)} \hfill \\<br /> = \prod\limits_n {{\mathbf{pp}}\left[ {x,mu1,mu2} \right]} \equiv {\mathbf{ppp}}\left[ {x,mu1,mu2} \right] \hfill \\ <br />\end{gathered} <br />\]](../latex_cache/45d43b605033a4aa279f5db4b6c5f8cb.png)
And in Mathematica, these mean:
mx=Join[N[Range[0,2,2/15]],N[Range[4,6,2/15]]]
Length[mx]
ListPlot[Table[{mx[[i]],1},{i,1,32}]]
p[x_,mu_]:=0.3989422804014327` * Exp[-(mu-x)^2/2];
pp[x_,mu1_,mu2_]:=.5 (p[x,mu1]+p[x,mu2]);
ppp[xx_,mu1_,mu2_]:=Module[
{ptot=1},
For[i=1,i<=Length[xx],i++,
ppar = pp[xx[[i]],mu1,mu2];
ptot *= ppar;
(*Print[xx[[i]],"\t",ppar];*)
];
Return[ptot];
];
Plot3D[ppp[mx,mu1,mu2],{mu1,0,6},{mu2,0,6},PlotRange->{0,10^-25}];

ContourPlot[ppp[mx,mu1,mu2],{mu1,0,6},{mu2,0,6},{PlotRange->{0,10^-25},ContourLines->False,PlotPoints->250}];(*It may take a while with PlotPoints->250, so just begin with PlotPoints->25 *)
That’s all folks! (for today I guess 8) (and also, I know that I said next entry would be about the soft K-means two entries ago, but believe me, we’re coming to that, eventually 😉
Attachments: Mathematica notebook for this entry, MSWord Document (actually this one is intended for me, because in the future I may need them again)
Likelihood of Gaussian(s) – Scrap Notes
December 3, 2007 Posted by Emre S. Tasci
Given a set of N data x, ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaaca
% WG4baacaGL7bGaayzFaaWaa0baaSqaaiaadMgacqGH9aqpcaaIXaaa
% baGaamOtaaaaaaa!3CCA!
\[
{\left\{ x \right\}_{i = 1}^N }
\]](../latex_cache/36f475828683a171a142690beecf0de0.png) , the optimal parameters for a Gaussian Probability Distribution Function defined as:
, the optimal parameters for a Gaussian Probability Distribution Function defined as:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6
% gadaWadaqaaiGaccfadaqadaqaamaaeiaabaWaaiWaaeaacaWG4baa
% caGL7bGaayzFaaWaa0baaSqaaiaadMgacqGH9aqpcaaIXaaabaGaam
% OtaaaaaOGaayjcSdGaeqiVd0Maaiilaiabeo8aZbGaayjkaiaawMca
% aaGaay5waiaaw2faaiabg2da9iabgkHiTiaad6eaciGGSbGaaiOBam
% aabmaabaWaaOaaaeaacaaIYaGaeqiWdahaleqaaOGaeq4WdmhacaGL
% OaGaayzkaaGaeyOeI0YaaSGbaeaadaWadaqaaiaad6eadaqadaqaai
% abeY7aTjabgkHiTiqadIhagaqeaaGaayjkaiaawMcaamaaCaaaleqa
% baGaaGOmaaaakiabgUcaRiaadofaaiaawUfacaGLDbaaaeaacaaIYa
% Gaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaaaaa!627A!
\[
\ln \left[ {\operatorname{P} \left( {\left. {\left\{ x \right\}_{i = 1}^N } \right|\mu ,\sigma } \right)} \right] = - N\ln \left( {\sqrt {2\pi } \sigma } \right) - {{\left[ {N\left( {\mu - \bar x} \right)^2 + S} \right]} \mathord{\left/
{\vphantom {{\left[ {N\left( {\mu - \bar x} \right)^2 + S} \right]} {2\sigma ^2 }}} \right.
\kern-\nulldelimiterspace} {2\sigma ^2 }}
\]](../latex_cache/2263a9a9668dc98fdb36e2a16e2f7d17.png)
are:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacq
% aH8oqBcaGGSaGaeq4WdmhacaGL7bGaayzFaaWaaSbaaSqaaiaad2ea
% caWGHbGaamiEaiaadMgacaWGTbGaamyDaiaad2gacaWGmbGaamyAai
% aadUgacaWGLbGaamiBaiaadMgacaWGObGaam4Baiaad+gacaWGKbaa
% beaakiabg2da9maacmaabaGabmiEayaaraGaaiilamaakaaabaWaaS
% GbaeaacaWGtbaabaGaamOtaaaaaSqabaaakiaawUhacaGL9baaaaa!5316!
\[
\left\{ {\mu ,\sigma } \right\}_{MaximumLikelihood} = \left\{ {\bar x,\sqrt {{S \mathord{\left/
{\vphantom {S N}} \right.
\kern-\nulldelimiterspace} N}} } \right\}
\]](../latex_cache/fb38a9b5139084cb4210f812c71f9232.png)
with the definitions
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmiEayaara
% Gaeyypa0ZaaSaaaeaadaaeWbqaaiaadIhadaWgaaWcbaGaamOBaaqa
% baaabaGaamOBaiabg2da9iaaigdaaeaacaWGobaaniabggHiLdaake
% aacaWGobaaaiaacYcacaWLjaGaam4uaiabg2da9maaqahabaWaaeWa
% aeaacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaeyOeI0IabmiEayaara
% aacaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaaqaaiaad6gacqGH
% 9aqpcaaIXaaabaGaamOtaaqdcqGHris5aaaa!5057!
\[
\bar x = \frac{{\sum\limits_{n = 1}^N {x_n } }}
{N}, & S = \sum\limits_{n = 1}^N {\left( {x_n - \bar x} \right)^2 }
\]](../latex_cache/2306d354e1dd738ba188a23c0295b260.png)
Let’s see this in an example:
Define the data set mx:
mx={1,7,9,10,15}
Calculate the optimal mu and sigma:
dN=Length[mx];
mu=Sum[mx[[i]]/dN,{i,1,dN}];
sig =Sqrt[Sum[(mx[[i]]-mu)^2,{i,1,dN}]/dN];
Print["mu = ",N[mu]];
Print["sigma = ",N[sig]];
Now, let’s see this Gaussian Distribution Function:
<<Statistics`NormalDistribution`
ndist=NormalDistribution[mu,sig];
MultipleListPlot[Table[{x,PDF[NormalDistribution[mu,sig],x]}, {x,0,20,.04}],Table[{mx[[i]], PDF[NormalDistribution[mu,sig],mx[[i]]]},{i,5}], {PlotRange->{Automatic,{0,.1}},PlotJoined->{False,False}, SymbolStyle->{GrayLevel[.8],GrayLevel[0]}}]
.png)

K-means Clustering – the hard way…
Posted by Emre S. Tasci
Clustering (or grouping) items using a defined similarity of selected properties is an effective way to classify the data, but also (and probably more important) aspect of clustering is to pick up abnormal pieces that are different from the other clusterable "herd". These exceptions may be the ones that we’re looking (or unlooking) for!
There is this simple clustering method called K-means Clustering. Suppose that you have N particles (atoms/people/books/shapes) defined by 3 properties (coordinates/{height, weight, eye color}/{title,number of sold copies,price}/{number of sides,color,size}). You want to classify them into K groups. A way of doing this involves the K-means Clustering algorithm. I have listed some examples to various items & their properties, but from now on, for clarity and easy visionalizing, I will stick to the first one (atoms with 3 coordinates, and while we’re at it, let’s take the coordinates as Cartesian coordinates).
The algorithm is simple: You introduce K means into the midst of the N items. Then apply the distance criteria for each means upon the data and relate the item to the nearest mean to it. Store this relations between the means and the items using a responsibility list (array, vector) for each means of size (dimension) N (number of items).
Let’s define some notation at this point:
- Designate the position of the kth mean by mk.
- Designate the position of the jth item by xj.
- Designate the responsibility list of the kth mean by rk such that the responsibility between that kth mean and the jth item is stored in the jth element of rk. If rk[j] is equal to 1, then it means that this mean is the closest mean to the item and 0 means that, some other mean is closer to this item so, it is not included in this mean’s responsibility.
The algorithm can be built in 3 steps:
0. Ä°nitialize the means. (Randomly or well calculated)
1. Analyze: Check the distances between the means and the items. Assign the items to their nearest mean’s responsibility list.
2. Move: Move the means to the center of mass of the items each is responsible for. (If a mean has no item it is responsible for, then just leave it where it is.)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCyBamaaBa
% aaleaacaWGRbaabeaakiabg2da9maalaaabaWaaabCaeaacaWGYbWa
% aSbaaSqaaiaadUgaaeqaaOWaamWaaeaacaWGPbaacaGLBbGaayzxaa
% GaeyyXICTaaCiEamaaBaaaleaacaWGPbaabeaaaeaacaWGPbGaeyyp
% a0JaaGymaaqaaiaad6eaa0GaeyyeIuoaaOqaamaaqahabaGaamOCam
% aaBaaaleaacaWGRbaabeaakmaadmaabaGaamyAaaGaay5waiaaw2fa
% aaWcbaGaamyAaiabg2da9iaaigdaaeaacaWGobaaniabggHiLdaaaa
% aa!5305!
\[
{\mathbf{m}}_k = \frac{{\sum\limits_{i = 1}^N {r_k \left[ i \right] \cdot {\mathbf{x}}_i } }}
{{\sum\limits_{i = 1}^N {r_k \left[ i \right]} }}
\]](../latex_cache/3afbfab99a3616e1407006b18917f01d.png)
3. Check: If one or more mean’s position has changed, then go to 1, if not exit.
That’s all about it. I have written a C++ code for this algorithm. It employs an object called kmean (can you guess what it is for? ) which has the properties and methods as:
class kmean
{
private:
unsigned int id,n;//"id" is for the unique identifier and "n" is the total number of items in the world.
double x,y,z;//coordinates of the mean
gsl_vector * r;//responsibility list of the mean
char buffer [150];//some dummy variable to use in the "whereis" method
unsigned int r_tott;//total number of data points this mean is responsible for
public:
kmean(int ID,double X, double Y, double Z,unsigned int N);
~kmean();
//kmean self(void);
int move(double X, double Y, double Z);//moves the mean to the point(X,Y,Z)
int calculate_distances(gsl_matrix *MatrixIN, int N, gsl_matrix *distances);//calculates the distances of the "N" items with their positions defined in "MatrixIN" and writes these values to the "distances" matrix
char * whereis(void);//returns the position of the mean in a formatted string
double XX(void) {return x;}//returns the x-component of the mean’s position
double YY(void) {return y;}//returns the y-component of the mean’s position
double ZZ(void) {return z;}//returns the z-component of the mean’s position
int II(void) {return id;}//returns the mean’s id
int NN(void) {return n;}//returns the number of items in the world (as the mean knows it)
int RR(void);//prints out the responsibility list (used for debugging purposes actually)
gsl_vector * RRV(void) {return r;}//returns the responsibility list
int set_r(int index, bool included);//sets the "index"th element of the responsibility list as the bool "included". (ie, registers the "index". item as whether it belongs or not belongs to the mean)
int moveCoM(gsl_matrix *MatrixIN);//moves the mean to the center of mass of the items it is responsible for
int RTOT(void) {return r_tott;}//returns the total number of items the mean is responsible for
};
int check_distances(gsl_matrix* distances, int numberOfWorldElements, kmean **means);//checks the "distances" matrix elements for the means in the "means" array and registers each item in the responsibility list of the nearest mean.
double distance(double a1, double a2,double a3,double b1,double b2,double b3);//distance criteria is defined with this function
Now that we have the essential kmean object, the rest of the code is actually just details. Additionaly, I’ve included a random world generator (and by world, I mean N items and their 3 coordinates, don’t be misled). So essentialy, in the main code, we have the following lines for the analyze section:
for (i=0;i<dK;i++)
means[i]->calculate_distances(m,dN,distances);
check_distances(distances,dN,means);
which first calculates the distances between each mean (defined as elements of the means[] array) and item (defined as the rows of the m matrice with dNx4 dimension (1st col: id, cols 2,3,4: coordinates) and writes the distances into the distances matrice (of dimensions dNxdK) via the calculate_distances(…) method. dN is the total number of items and dK is the total number of means. Then analyzes the distances matrice, finds the minimum of each row (because rows represent the items and columns represent the means) and registers the item as 1 in the nearest means’s responsibility list, and as 0 in the other means’ lists via the check_distances(…) method.
Then, the code executes its move section:
for(i=0; i<dK; i++)
{
means[i]->moveCoM(m);
[…]
}
which simply moves the means to the center of mass of the items they’re responsible for. This section is followed by the checkSufficiency section which simply decides if we should go for one more iteration or just call it quits.
counter++;
if(counter>=dMaxCounter) {f_maxed = true;goto finalize;}
gsl_matrix_sub(prevMeanPositions,currMeanPositions);
if(gsl_matrix_isnull(prevMeanPositions)) goto finalize;
[…]
goto analyze;
as you can see, it checks for two things: whether a predefined iteration limit has been reached or, if at least one (two 😉 of the means moved in the last iteration. finalize is the section where some tidying up is processed (freeing up the memory, closing of the open files, etc…)
The code uses two external libraries: the Gnu Scientific Library (GSL) and the Templatized C++ Command Line Parser Library (TCLAP). While GSL is essential for the matrix operations and the structs I have intensely used, TCLAP is used for a practical and efficient solution considering the argument parsing. If you have enough reasons for reading this blog and this entry up to this line and (a tiny probability but, anyway) have not heard about GSL before, you MUST check it out. For TCLAP, I can say that, it has become a habit for me since it is very easy to use. About what it does, it enables you to enable the external variables that may be defined in the command execution even if you know nothing about argument parsing. I strictly recommend it (and thank to Michael E. Smoot again 8).
The program can be invoked with the following arguments:
D:\source\cpp\Kmeans>kmeans –help
USAGE:
kmeans -n <int> -k <int> [-s <unsigned long int>] [-o <output file>]
[-m <int>] [-q] [–] [–version] [-h]
Where:
-n <int>, –numberofelements <int>
(required) total number of elements (required)
-k <int>, –numberofmeans <int>
(required) total number of means (required)
-s <unsigned long int>, –seed <unsigned long int>
seed for random number generator (default: timer)
-o <output file>, –output <output file>
output file basename (default: "temp")
-m <int>, –maxcounter <int>
maximum number of steps allowed (default: 30)
-q, –quiet
no output to screen is generated
–, –ignore_rest
Ignores the rest of the labeled arguments following this flag.
–version
Displays version information and exits.
-h, –help
Displays usage information and exits.
K-Means by Emre S. Tasci, <…@tudelft.nl> 2007
The code outputs various files:
<project-name>.means.txt : Coordinates of the means evolution in the iterations
<project-name>.meansfinal.txt : Final coordinates of the means
<project-name>.report : A summary of the process
<project-name>.world.dat : The "world" matrice in Mathematica Write format
<project-name>.world.txt : Coordinates of the items (ie, the "world" matrice in XYZ format)
<project-name>-mean-#-resp.txt : Coordinates of the items belonging to the #. mean
and one last remark to those who are not that much accustomed to coding in C++: Do not forget to include the "include" directories!
Check the following command and modify it according to your directory locations (I do it in the Windows-way 🙂
g++ -o kmeans.exe kmeans.cpp -I c:\GnuWin32\include -L c:\GnuWin32\lib -lgsl -lgslcblas -lm
(If you are not keen on modifying the code and your operating system is Windows, you also have the option to download the compiled binary from here)
The source files can be obtained from here.
And, the output of an example with 4000 items and 20 means can be obtained here, while the output of a tinier example with 100 items and 2 means can be obtained here.
I’m planning to continue with the soft version of the K-Means algorithm for the next time…
References: Information Theory, Inference, and Learning Algorithms by David MacKay
Bayesian Probabilities & Inference – Another example
November 27, 2007 Posted by Emre S. Tasci
Yesterday, I told my battalion-buddy, Andy about the pregnancy example and, he recalled another example, with the shuffling of the three cups and a ball in one of them. The situation is proposed like this:
The dealer puts the ball in one of the cups and shuffles it so fast that at one point you lose the track and absolutely have no idea which cup has the ball. So, you pick a cup randomly (let’s say the first cup) but for the moment, don’t look inside. At this point, the dealer says, he will remove one of the remaining two cups and he guarantees you that, the one he removes does not have the ball. He even bestows you the opportunity to change your mind and pick the other one if you like. The question is this: Should you
a) Stick to the one you’ve selected or,
b) Switch to the other one or,
c) (a) or (b) – what does it matter?
Today, while I was studying MacKay’s book Theory, Inference, and Learning Algorithms, I came upon to the same example and couldn’t refrain myself from including it on this blog.
First, let’s solve the problem with simple notation. Let’s say that, initially we have picked the first cup, the probability that this cup has the ball is 1/3. There are two possibilities: Whether in reality the 1st cup has the ball indeed, or not.
i) 1st cup has the ball (1/3 of all the times): With this situation, it doesn’t matter which of the two cups remaining is removed.
ii) 1st cup doesn’t have the ball (2/3 of all the times): This time, the dealer removes the one, and the remaining cup has the ball.
So, to summarize, left with the two cups, there’s a 1/3 probability that the ball is within the cup we have chosen in the beginning while there’s the 2/3 probability that the ball is within the other cup. So, switching is the advantegous (did I spell it correctly? Don’t think so.. ) / To put it in other words: option (b) must be preffered to option (a) and actually, option (c) is wrong.
Now, let’s compute the same thing with the formal notations:
Let Hi be define the situation that the ball is in cup i. D denotes the removed cup (either 2 or 3). Now, initially the ball can be in any of the three cups with equal probabilities so
![Formula: % MathType!MTEF!2!1!+-<br />
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm<br />
% aabaGaamisamaaBaaaleaacaaIXaaabeaaaOGaayjkaiaawMcaaiab<br />
% g2da9iaadcfadaqadaqaaiaadIeadaWgaaWcbaGaaGymaaqabaaaki<br />
% aawIcacaGLPaaacqGH9aqpcaWGqbWaaeWaaeaacaWGibWaaSbaaSqa<br />
% aiaaigdaaeqaaaGccaGLOaGaayzkaaGaeyypa0ZaaSqaaSqaaiaaig<br />
% daaeaacaaIZaaaaaaa!46E7!<br />
\[<br />
P\left( {H_1 } \right) = P\left( {H_1 } \right) = P\left( {H_1 } \right) = \tfrac{1}<br />
{3}<br />
\]<br />](../latex_cache/ad1a07b9d6fc3e0f068887aff30c0ec3.png)
Now, since we have selected the 1st cup, either 2nd or the 3rd cup will be removed. And we have three cases for the ball position:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaqGaaeaafa
% qabeGabaaabaGaamiuaiaacIcacaWGebGaeyypa0JaaGOmaiaacYha
% caWGibWaaSbaaSqaaiaaigdaaeqaaOGaaiykaiabg2da9maaleaale
% aacaaIXaaabaGaaGOmaaaaaOqaaiaadcfacaGGOaGaamiraiabg2da
% 9iaaiodacaGG8bGaamisamaaBaaaleaacaaIXaaabeaakiaacMcacq
% GH9aqpdaWcbaWcbaGaaGymaaqaaiaaikdaaaaaaaGccaGLiWoafaqa
% beGabaaabaGaamiuaiaacIcacaWGebGaeyypa0JaaGOmaiaacYhaca
% WGibWaaSbaaSqaaiaaikdaaeqaaOGaaiykaiabg2da9iaaicdaaeaa
% caWGqbGaaiikaiaadseacqGH9aqpcaaIZaGaaiiFaiaadIeadaWgaa
% WcbaGaaGOmaaqabaGccaGGPaGaeyypa0JaaGymaaaadaabbaqaauaa
% beqaceaaaeaacaWGqbGaaiikaiaadseacqGH9aqpcaaIYaGaaiiFai
% aadIeadaWgaaWcbaGaaG4maaqabaGccaGGPaGaeyypa0JaaGymaaqa
% aiaadcfacaGGOaGaamiraiabg2da9iaaiodacaGG8bGaamisamaaBa
% aaleaacaaIZaaabeaakiaacMcacqGH9aqpcaaIWaaaaaGaay5bSdaa
% aa!7259!
\[
\left. {\begin{array}{*{20}c}
{P(D = 2|H_1 ) = \tfrac{1}
{2}} \\
{P(D = 3|H_1 ) = \tfrac{1}
{2}} \\
\end{array} } \right|\begin{array}{*{20}c}
{P(D = 2|H_2 ) = 0} \\
{P(D = 3|H_2 ) = 1} \\
\end{array} \left| {\begin{array}{*{20}c}
{P(D = 2|H_3 ) = 1} \\
{P(D = 3|H_3 ) = 0} \\
\end{array} } \right.
\]](../latex_cache/4fc864c6872eb6452e816e7eadc00fdd.png)
The first column represents that the ball is in our selected cup, so it doesn’t matter which of the remaining cups the dealer will remove. Each of the remaining cup has the same probability to be removed which is 0.5. The second column is the situation when the ball is in the second cup. Since it is in the second cup, the dealer will be forced to remove the third cup (ie P(D=3|H2)=1 ).Third column is similar to the second column.
Let’s suppose that, the dealer removed the third cup. With the 3rd cup removed, the probability that the ball is in the i. cup is given by: (remember that Hi represents the situation that the ball is in the i. cup)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamisamaaBaaaleaacaWGPbaabeaakiaacYhacaWGebGaeyyp
% a0JaaG4maaGaayjkaiaawMcaaiabg2da9maalaaabaGaamiuamaabm
% aabaGaamiraiabg2da9iaaiodacaGG8bGaamisamaaBaaaleaacaWG
% PbaabeaaaOGaayjkaiaawMcaaiaadcfadaqadaqaaiaadIeadaWgaa
% WcbaGaamyAaaqabaaakiaawIcacaGLPaaaaeaacaWGqbWaaeWaaeaa
% caWGebGaeyypa0JaaG4maaGaayjkaiaawMcaaaaaaaa!4FF2!
\[
P\left( {H_i |D = 3} \right) = \frac{{P\left( {D = 3|H_i } \right)P\left( {H_i } \right)}}
{{P\left( {D = 3} \right)}}
\]](../latex_cache/34a6b3faa776ca6104636141b00e21d8.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaqGaaeaaca
% WGqbWaaeWaaeaacaWGibWaaSbaaSqaaiaaigdaaeqaaOGaaiiFaiaa
% dseacqGH9aqpcaaIZaaacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaada
% WcbaWcbaGaaGymaaqaaiaaikdaaaGccqGHflY1daWcbaWcbaGaaGym
% aaqaaiaaiodaaaaakeaacaWGqbWaaeWaaeaacaWGebGaeyypa0JaaG
% 4maaGaayjkaiaawMcaaaaaaiaawIa7aiaadcfadaqadaqaaiaadIea
% daWgaaWcbaGaaGOmaaqabaGccaGG8bGaamiraiabg2da9iaaiodaai
% aawIcacaGLPaaacqGH9aqpdaWcaaqaaiaaigdacqGHflY1daWcbaWc
% baGaaGymaaqaaiaaiodaaaaakeaacaWGqbWaaeWaaeaacaWGebGaey
% ypa0JaaG4maaGaayjkaiaawMcaaaaadaabbaqaaiaadcfadaqadaqa
% aiaadIeadaWgaaWcbaGaaGOmaaqabaGccaGG8bGaamiraiabg2da9i
% aaiodaaiaawIcacaGLPaaacqGH9aqpdaWcaaqaaiaaicdacqGHflY1
% daWcbaWcbaGaaGymaaqaaiaaiodaaaaakeaacaWGqbWaaeWaaeaaca
% WGebGaeyypa0JaaG4maaGaayjkaiaawMcaaaaaaiaawEa7aaaa!70DB!
\[
\left. {P\left( {H_1 |D = 3} \right) = \frac{{\tfrac{1}
{2} \cdot \tfrac{1}
{3}}}
{{P\left( {D = 3} \right)}}} \right|P\left( {H_2 |D = 3} \right) = \frac{{1 \cdot \tfrac{1}
{3}}}
{{P\left( {D = 3} \right)}}\left| {P\left( {H_2 |D = 3} \right) = \frac{{0 \cdot \tfrac{1}
{3}}}
{{P\left( {D = 3} \right)}}} \right.
\]](../latex_cache/d28519eef1c192c02bd65d0840ec790b.png)
for our purposes, P(D=3) is not relevant, because we are looking for the comparison of the first two probabilities (P(D=3) = 0.5, by the way since it is either D=2 or D=3).
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca
% WGqbWaaeWaaeaacaWGibWaaSbaaSqaaiaaigdaaeqaaOGaaiiFaiaa
% dseacqGH9aqpcaaIZaaacaGLOaGaayzkaaaabaGaamiuamaabmaaba
% GaamisamaaBaaaleaacaaIYaaabeaakiaacYhacaWGebGaeyypa0Ja
% aG4maaGaayjkaiaawMcaaaaacqGH9aqpdaWcaaqaaiaaigdaaeaaca
% aIYaaaaaaa!47DB!
\[
\frac{{P\left( {H_1 |D = 3} \right)}}
{{P\left( {H_2 |D = 3} \right)}} = \frac{1}
{2}
\]](../latex_cache/b0d88841dfc32e38f97cc991beb7a930.png)
meaning that it is 2 times more likely that the ball is in the other cup than the one we initially had selected.
Like John, Jo’s funny boyfriend in the previous bayesian example, used in context to show the unlikeliness of the "presumed" logical derivation, MacKay introduces the concept of one million cups instead of the three. Suppose you have selected one cup among the one million cups. Then, the dealer removes 999,998 cups and you’re left with the one you’ve initially chosen and the 432,238th cup. Would you now switch, or stick to the one you had chosen?
Bayesian Inference – An introduction with an example
November 26, 2007 Posted by Emre S. Tasci
Suppose that Jo (of Example 2.3 in MacKay’s previously mentioned book), decided to take a test to see whether she’s pregnant or not. She applies a test that is 95% reliable, that is if she’s indeed pregnant, than there is a 5% chance that the test will result otherwise and if she’s indeed NOT pregnant, the test will tell her that she’s pregnant again by a 5% chance (The other two options are test concluding as positive on pregnancy when she’s indeed pregnant by 95% of all the time, and test reports negative on pregnancy when she’s actually not pregnant by again 95% of all the time). Suppose that she is applying contraceptive drug with a 1% fail ratio.
Now comes the question: Jo takes the test and the test says that she’s pregnant. Now what is the probability that she’s indeed pregnant?
I would definitely not write down this example if the answer was 95% percent as you may or may not have guessed but, it really is tempting to guess the probability as 95% the first time.
The solution (as given in the aforementioned book) is:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaabbeaacaWGqb
% GaaiikaiaadshacaWGLbGaam4CaiaadshacaGG6aGaaGymaiaacYha
% caWGWbGaamOCaiaadwgacaWGNbGaaiOoaiaaigdacaGGPaGaeyypa0
% ZaaSaaaeaacaWGqbGaaiikaiaadchacaWGYbGaamyzaiaadEgacaGG
% 6aGaaGymaiaacYhacaWG0bGaamyzaiaadohacaWG0bGaaiOoaiaaig
% dacaGGPaGaamiuaiaacIcacaWGWbGaamOCaiaadwgacaWGNbGaaiOo
% aiaaigdacaGGPaaabaGaamiuaiaacIcacaWG0bGaamyzaiaadohaca
% WG0bGaaiOoaiaaigdacaGGPaaaaaqaaiabg2da9maalaaabaGaamiu
% aiaacIcacaWGWbGaamOCaiaadwgacaWGNbGaaiOoaiaaigdacaGG8b
% GaamiDaiaadwgacaWGZbGaamiDaiaacQdacaaIXaGaaiykaiaadcfa
% caGGOaGaamiCaiaadkhacaWGLbGaam4zaiaacQdacaaIXaGaaiykaa
% qaamaaqafabaGaamiuaiaacIcacaWG0bGaamyzaiaadohacaWG0bGa
% aiOoaiaaigdacaGG8bGaamiCaiaadkhacaWGLbGaam4zaiaacQdaca
% WGPbGaaiykaiaadcfacaGGOaGaamiCaiaadkhacaWGLbGaam4zaiaa
% cQdacaWGPbGaaiykaaWcbaGaamyAaaqab0GaeyyeIuoaaaaakeaacq
% GH9aqpdaWcaaqaaiaaicdacaGGUaGaaGyoaiaaiwdacqGHxdaTcaaI
% WaGaaiOlaiaaicdacaaIXaaabaGaaGimaiaac6cacaaI5aGaaGynai
% abgEna0kaaicdacaGGUaGaaGimaiaaigdacqGHRaWkcaaIWaGaaiOl
% aiaaicdacaaI1aGaey41aqRaaGimaiaac6cacaaI5aGaaGyoaaaaae
% aacqGH9aqpcaaIWaGaaiOlaiaaigdacaaI2aaaaaa!ADD3!
\[
\begin{gathered}
P(test:1|preg:1) = \frac{{P(preg:1|test:1)P(preg:1)}}
{{P(test:1)}} \\
= \frac{{P(preg:1|test:1)P(preg:1)}}
{{\sum\limits_i {P(test:1|preg:i)P(preg:i)} }} \\
= \frac{{0.95 \times 0.01}}
{{0.95 \times 0.01 + 0.05 \times 0.99}} \\
= 0.16 \\
\end{gathered}
\]](../latex_cache/6453cf859b172f767097226e22e99927.png)
where P(b:bj|a:ai) represents the probability of b having the value bj given that a=ai. So Jo has P(test:1|preg=1) = 16% meaning that given that Jo is actually pregnant, the test would give the positive result by a probability of 16%. So we took into account both the test’s and the contra-ceptive’s reliabilities. If this doesn’t make sense and you still want to stick with the somehow more logical looking 95%, think the same example but this time starring John, Jo’s humorous boyfriend who as a joke applied the test and came with a positive result on pregnancy. Now, do you still say that John is 95% pregnant? I guess not Just plug in 0 for P(preg:1) to the equation above and enjoy the outcoming likelihood of John being non-pregnant equaling to 0…
The thing to keep in mind is the probability of a being some value ai when b is bj is not equal to the probability of b being bj when a is equal to ai.


