Some “trivial” derivations
December 4, 2007 Posted by Emre S. Tasci
Information Theory, Inference, and Learning Algorithms by David MacKay, Exercise 22.5:
A random variable x is assumed to have a probability distribution that is a mixture of two Gaussians,
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamiEaiaacYhacqaH8oqBdaWgaaWcbaGaaGymaaqabaGccaGG
% SaGaeqiVd02aaSbaaSqaaiaaikdaaeqaaOGaaiilaiabeo8aZbGaay
% jkaiaawMcaaiabg2da9maadmaabaWaaabCaeaacaWGWbWaaSbaaSqa
% aiaadUgaaeqaaOWaaSaaaeaacaaIXaaabaWaaOaaaeaacaaIYaGaeq
% iWdaNaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaqabaaaaOGaciyzaiaa
% cIhacaGGWbWaaeWaaeaacqGHsisldaWcaaqaamaabmaabaGaamiEai
% abgkHiTiabeY7aTnaaBaaaleaacaWGRbaabeaaaOGaayjkaiaawMca
% amaaCaaaleqabaGaaGOmaaaaaOqaaiaaikdacqaHdpWCdaahaaWcbe
% qaaiaaikdaaaaaaaGccaGLOaGaayzkaaaaleaacaWGRbGaeyypa0Ja
% aGymaaqaaiaaikdaa0GaeyyeIuoaaOGaay5waiaaw2faaaaa!63A5!
\[
P\left( {x|\mu _1 ,\mu _2 ,\sigma } \right) = \left[ {\sum\limits_{k = 1}^2 {p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x - \mu _k } \right)^2 }}
{{2\sigma ^2 }}} \right)} } \right]
\]](../latex_cache/02ffa24cafcda9c52b21f37689acad79.png)
where the two Gaussians are given the labels k = 1 and k = 2; the prior probability of the class label k is {p1 = 1/2, p2 = 1/2}; ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacq
% aH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawUhacaGL9baaaaa!3AFA!
\[
{\left\{ {\mu _k } \right\}}
\]](../latex_cache/63181a36e52687072bbbd54c4488895f.png) are the means of the two Gaussians; and both have standard deviation sigma. For brevity, we denote these parameters by
are the means of the two Gaussians; and both have standard deviation sigma. For brevity, we denote these parameters by
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCiUdiabgg
% Mi6oaacmaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam4Aaaqabaaa
% kiaawUhacaGL9baacaGGSaGaeq4WdmhacaGL7bGaayzFaaaaaa!42AB!
\[
{\mathbf{\theta }} \equiv \left\{ {\left\{ {\mu _k } \right\},\sigma } \right\}
\]](../latex_cache/0872f8d876f08afa90626cfb8bfd6165.png)
A data set consists of N points ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaaca
% WG4bWaaSbaaSqaaiaad6gaaeqaaaGccaGL7bGaayzFaaWaa0baaSqa
% aiaad6gacqGH9aqpcaaIXaaabaGaamOtaaaaaaa!3DF8!
\[
\left\{ {x_n } \right\}_{n = 1}^N
\]](../latex_cache/5960b3e63e93b0eadb7f05b6597dc081.png) which are assumed to be independent samples from the distribution. Let kn denote the unknown class label of the nth point.
which are assumed to be independent samples from the distribution. Let kn denote the unknown class label of the nth point.
Assuming that ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacq
% aH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawUhacaGL9baaaaa!3AFA!
\[
{\left\{ {\mu _k } \right\}}
\]](../latex_cache/63181a36e52687072bbbd54c4488895f.png) and
and ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdmhaaa!37B0!
\[
\sigma
\]](../latex_cache/0bcead44095f85d706d5bd0d3ee69019.png) are known, show that the posterior probability of the class label kn of the nth point can be written as
are known, show that the posterior probability of the class label kn of the nth point can be written as
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb
% WaaeWaaeaadaabcaqaaiaadUgadaWgaaWcbaGaamOBaaqabaGccqGH
% 9aqpcaaIXaaacaGLiWoacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaai
% ilaiaahI7aaiaawIcacaGLPaaacqGH9aqpdaWcaaqaaiaaigdaaeaa
% caaIXaGaey4kaSIaciyzaiaacIhacaGGWbWaamWaaeaacqGHsislda
% qadaqaaiabeM8a3naaBaaaleaacaaIXaaabeaakiaadIhadaWgaaWc
% baGaamOBaaqabaGccqGHRaWkcqaHjpWDdaWgaaWcbaGaaGimaaqaba
% aakiaawIcacaGLPaaaaiaawUfacaGLDbaaaaaabaGaamiuamaabmaa
% baWaaqGaaeaacaWGRbWaaSbaaSqaaiaad6gaaeqaaOGaeyypa0JaaG
% OmaaGaayjcSdGaamiEamaaBaaaleaacaWGUbaabeaakiaacYcacaWH
% 4oaacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaaIXaaabaGaaGymai
% abgUcaRiGacwgacaGG4bGaaiiCamaadmaabaGaey4kaSYaaeWaaeaa
% cqaHjpWDdaWgaaWcbaGaaGymaaqabaGccaWG4bWaaSbaaSqaaiaad6
% gaaeqaaOGaey4kaSIaeqyYdC3aaSbaaSqaaiaaicdaaeqaaaGccaGL
% OaGaayzkaaaacaGLBbGaayzxaaaaaaaaaa!7422!
\[
\begin{gathered}
P\left( {\left. {k_n = 1} \right|x_n ,{\mathbf{\theta }}} \right) = \frac{1}
{{1 + \exp \left[ { - \left( {\omega _1 x_n + \omega _0 } \right)} \right]}} \hfill \\
P\left( {\left. {k_n = 2} \right|x_n ,{\mathbf{\theta }}} \right) = \frac{1}
{{1 + \exp \left[ { + \left( {\omega _1 x_n + \omega _0 } \right)} \right]}} \hfill \\
\end{gathered}
\]](../latex_cache/f1256d14a59790f5d35c2bedc4a49bbc.png)
and give expressions for ![Formula: \[\omega _1 \]](../latex_cache/9b85d537fe39f505e5182913d97fdfb8.png) and
and ![Formula: \[\omega _0 \]](../latex_cache/dfa670f67ce3c9849cc5c143a295efac.png) .
.
Derivation:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaWaaqGaaeaacaWGRbWaaSbaaSqaaiaad6gaaeqaaOGaeyypa0Ja
% aGymaaGaayjcSdGaamiEamaaBaaaleaacaWGUbaabeaakiaacYcaca
% WH4oaacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaWGqbWaaeWaaeaa
% caWG4bWaaSbaaSqaaiaad6gaaeqaaOWaaqqaaeaacaWGRbWaaSbaaS
% qaaiaad6gaaeqaaOGaeyypa0JaaGymaiaacYcacaWH4oaacaGLhWoa
% aiaawIcacaGLPaaacaWGqbWaaeWaaeaacaWGRbWaaSbaaSqaaiaad6
% gaaeqaaOGaeyypa0JaaGymaaGaayjkaiaawMcaaaqaaiaadcfadaqa
% daqaaiaadIhadaWgaaWcbaGaamOBaaqabaaakiaawIcacaGLPaaaaa
% aaaa!598D!
\[
P\left( {\left. {k_n = 1} \right|x_n ,{\mathbf{\theta }}} \right) = \frac{{P\left( {x_n \left| {k_n = 1,{\mathbf{\theta }}} \right.} \right)P\left( {k_n = 1} \right)}}
{{P\left( {x_n } \right)}}
\]](../latex_cache/a715c20187b7d1333ddd7eac5d275abb.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamiEamaaBaaaleaacaWGUbaabeaakmaaeeaabaGaam4Aamaa
% BaaaleaacaWGUbaabeaakiabg2da9iaaigdacaGGSaGaaCiUdaGaay
% 5bSdaacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaaIXaaabaWaaOaa
% aeaacaaIYaGaeqiWdaNaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaqaba
% aaaOGaciyzaiaacIhacaGGWbWaaeWaaeaacqGHsisldaWcaaqaamaa
% bmaabaGaamiEamaaBaaaleaacaWGUbaabeaakiabgkHiTiabeY7aTn
% aaBaaaleaacaaIXaaabeaaaOGaayjkaiaawMcaamaaCaaaleqabaGa
% aGOmaaaaaOqaaiaaikdacqaHdpWCdaahaaWcbeqaaiaaikdaaaaaaa
% GccaGLOaGaayzkaaaaaa!59EC!
\[
P\left( {x_n \left| {k_n = 1,{\mathbf{\theta }}} \right.} \right) = \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x_n - \mu _1 } \right)^2 }}
{{2\sigma ^2 }}} \right)
\]](../latex_cache/fad7cf1dcafb714f7a176d734a527a09.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaGaamiEamaaBaaaleaacaWGUbaabeaaaOGaayjkaiaawMcaaiab
% g2da9maaqahabaGaamiuamaabmaabaWaaqGaaeaacaWG4bWaaSbaaS
% qaaiaad6gaaeqaaaGccaGLiWoacaWGRbWaaSbaaSqaaiaad6gaaeqa
% aOGaeyypa0JaamyAaiaacYcacaWH4oaacaGLOaGaayzkaaGaamiuam
% aabmaabaGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaadMga
% aiaawIcacaGLPaaaaSqaaiaadMgacqGH9aqpcaaIXaaabaGaaGOmaa
% qdcqGHris5aaaa!53AA!
\[
P\left( {x_n } \right) = \sum\limits_{i = 1}^2 {P\left( {\left. {x_n } \right|k_n = i,{\mathbf{\theta }}} \right)P\left( {k_n = i} \right)}
\]](../latex_cache/4552f718d3d4a5d314db5eec6e935fe6.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb
% WaaeWaaeaadaabcaqaaiaadUgadaWgaaWcbaGaamOBaaqabaGccqGH
% 9aqpcaaIXaaacaGLiWoacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaai
% ilaiaahI7aaiaawIcacaGLPaaacqGH9aqpdaWcaaqaamaalaaabaGa
% aGymaaqaamaakaaabaGaaGOmaiabec8aWjabeo8aZnaaCaaaleqaba
% GaaGOmaaaaaeqaaaaakiGacwgacaGG4bGaaiiCamaabmaabaGaeyOe
% I0YaaSaaaeaadaqadaqaaiaadIhadaWgaaWcbaGaamOBaaqabaGccq
% GHsislcqaH8oqBdaWgaaWcbaGaaGymaaqabaaakiaawIcacaGLPaaa
% daahaaWcbeqaaiaaikdaaaaakeaacaaIYaGaeq4Wdm3aaWbaaSqabe
% aacaaIYaaaaaaaaOGaayjkaiaawMcaaiaadcfadaqadaqaaiaadUga
% daWgaaWcbaGaamOBaaqabaGccqGH9aqpcaaIXaaacaGLOaGaayzkaa
% aabaWaaSaaaeaacaaIXaaabaWaaOaaaeaacaaIYaGaeqiWdaNaeq4W
% dm3aaWbaaSqabeaacaaIYaaaaaqabaaaaOGaciyzaiaacIhacaGGWb
% WaaeWaaeaacqGHsisldaWcaaqaamaabmaabaGaamiEamaaBaaaleaa
% caWGUbaabeaakiabgkHiTiabeY7aTnaaBaaaleaacaaIXaaabeaaaO
% GaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaOqaaiaaikdacqaH
% dpWCdaahaaWcbeqaaiaaikdaaaaaaaGccaGLOaGaayzkaaGaamiuam
% aabmaabaGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaaigda
% aiaawIcacaGLPaaacqGHRaWkdaWcaaqaaiaaigdaaeaadaGcaaqaai
% aaikdacqaHapaCcqaHdpWCdaahaaWcbeqaaiaaikdaaaaabeaaaaGc
% ciGGLbGaaiiEaiaacchadaqadaqaaiabgkHiTmaalaaabaWaaeWaae
% aacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaeyOeI0IaeqiVd02aaSba
% aSqaaiaaikdaaeqaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaIYa
% aaaaGcbaGaaGOmaiabeo8aZnaaCaaaleqabaGaaGOmaaaaaaaakiaa
% wIcacaGLPaaacaWGqbWaaeWaaeaacaWGRbWaaSbaaSqaaiaad6gaae
% qaaOGaeyypa0JaaGOmaaGaayjkaiaawMcaaaaaaeaacqGH9aqpdaWc
% aaqaaiaaigdaaeaacaaIXaGaey4kaSIaciyzaiaacIhacaGGWbWaae
% WaaeaacqGHsisldaWcaaqaamaabmaabaGaamiEamaaBaaaleaacaWG
% UbaabeaakiabgkHiTiabeY7aTnaaBaaaleaacaaIYaaabeaaaOGaay
% jkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaOqaaiaaikdacqaHdpWC
% daahaaWcbeqaaiaaikdaaaaaaOGaey4kaSYaaSaaaeaadaqadaqaai
% aadIhadaWgaaWcbaGaamOBaaqabaGccqGHsislcqaH8oqBdaWgaaWc
% baGaaGymaaqabaaakiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaa
% aakeaacaaIYaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaaaOGaayjk
% aiaawMcaamaabmaabaWaaSaaaeaacaaIXaGaeyOeI0Iaamiuamaabm
% aabaGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaaigdaaiaa
% wIcacaGLPaaaaeaacaWGqbWaaeWaaeaacaWGRbWaaSbaaSqaaiaad6
% gaaeqaaOGaeyypa0JaaGymaaGaayjkaiaawMcaaaaaaiaawIcacaGL
% Paaaaaaaaaa!CC7A!
\[
\begin{gathered}
P\left( {\left. {k_n = 1} \right|x_n ,{\mathbf{\theta }}} \right) = \frac{{\frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x_n - \mu _1 } \right)^2 }}
{{2\sigma ^2 }}} \right)P\left( {k_n = 1} \right)}}
{{\frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x_n - \mu _1 } \right)^2 }}
{{2\sigma ^2 }}} \right)P\left( {k_n = 1} \right) + \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left( { - \frac{{\left( {x_n - \mu _2 } \right)^2 }}
{{2\sigma ^2 }}} \right)P\left( {k_n = 2} \right)}} \hfill \\
= \frac{1}
{{1 + \exp \left( { - \frac{{\left( {x_n - \mu _2 } \right)^2 }}
{{2\sigma ^2 }} + \frac{{\left( {x_n - \mu _1 } \right)^2 }}
{{2\sigma ^2 }}} \right)\left( {\frac{{1 - P\left( {k_n = 1} \right)}}
{{P\left( {k_n = 1} \right)}}} \right)}} \hfill \\
\end{gathered}
\]](../latex_cache/1e6fdf2c5d24e2be5c59df57c14121ec.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS
% aaaeaacaaIXaaabaGaaGymaiabgUcaRiGacwgacaGG4bGaaiiCamaa
% dmaabaGaeyOeI0YaaeWaaeaadaqadaqaamaalaaabaWaaeWaaeaacq
% aH8oqBdaWgaaWcbaGaaGymaaqabaGccqGHsislcqaH8oqBdaWgaaWc
% baGaaGOmaaqabaaakiaawIcacaGLPaaaaeaacqaHdpWCdaahaaWcbe
% qaaiaaikdaaaaaaaGccaGLOaGaayzkaaGaamiEamaaBaaaleaacaWG
% UbaabeaakiabgUcaRmaabmaabaWaaSaaaeaadaqadaqaaiabeY7aTn
% aaBaaaleaacaaIYaaabeaakmaaCaaaleqabaGaaGOmaaaakiabgkHi
% TiabeY7aTnaaBaaaleaacaaIXaaabeaakmaaCaaaleqabaGaaGOmaa
% aaaOGaayjkaiaawMcaaaqaaiaaikdacqaHdpWCdaahaaWcbeqaaiaa
% ikdaaaaaaaGccaGLOaGaayzkaaaacaGLOaGaayzkaaaacaGLBbGaay
% zxaaaaaaaa!5E70!
\[
= \frac{1}
{{1 + \exp \left[ { - \left( {\left( {\frac{{\left( {\mu _1 - \mu _2 } \right)}}
{{\sigma ^2 }}} \right)x_n + \left( {\frac{{\left( {\mu _2 ^2 - \mu _1 ^2 } \right)}}
{{2\sigma ^2 }}} \right)} \right)} \right]}}
\]](../latex_cache/2cb3dc1005d19db77232acac5cfde110.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS
% aaaeaacaaIXaaabaGaaGymaiabgUcaRiGacwgacaGG4bGaaiiCamaa
% dmaabaGaeyOeI0YaaeWaaeaacqaHjpWDdaWgaaWcbaGaaGymaaqaba
% GccaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaey4kaSIaeqyYdC3aaSba
% aSqaaiaaicdaaeqaaaGccaGLOaGaayzkaaaacaGLBbGaayzxaaaaaa
% aa!4921!
\[
= \frac{1}
{{1 + \exp \left[ { - \left( {\omega _1 x_n + \omega _0 } \right)} \right]}}
\]](../latex_cache/fad0a283da2a75ecc80ae95039e225d9.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyYdC3aaS
% baaSqaaiaaigdaaeqaaOGaeyyyIO7aaSaaaeaadaqadaqaaiabeY7a
% TnaaBaaaleaacaaIXaaabeaakiabgkHiTiabeY7aTnaaBaaaleaaca
% aIYaaabeaaaOGaayjkaiaawMcaaaqaaiabeo8aZnaaCaaaleqabaGa
% aGOmaaaaaaGccaGG7aGaaCzcaiabeM8a3naaBaaaleaacaaIWaaabe
% aakiabggMi6oaalaaabaWaaeWaaeaacqaH8oqBdaWgaaWcbaGaaGOm
% aaqabaGcdaahaaWcbeqaaiaaikdaaaGccqGHsislcqaH8oqBdaWgaa
% WcbaGaaGymaaqabaGcdaahaaWcbeqaaiaaikdaaaaakiaawIcacaGL
% PaaaaeaacaaIYaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaaaaa!5809!
\[
\omega _1 \equiv \frac{{\left( {\mu _1 - \mu _2 } \right)}}
{{\sigma ^2 }}; & \omega _0 \equiv \frac{{\left( {\mu _2 ^2 - \mu _1 ^2 } \right)}}
{{2\sigma ^2 }}
\]](../latex_cache/ecb970e7b19db2f916b89d7f4f9ff62f.png)
Assume now that the means ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacq
% aH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawUhacaGL9baaaaa!3AFA!
\[
{\left\{ {\mu _k } \right\}}
\]](../latex_cache/63181a36e52687072bbbd54c4488895f.png) are not known, and that we wish to infer them from the data
are not known, and that we wish to infer them from the data ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaaca
% WG4bWaaSbaaSqaaiaad6gaaeqaaaGccaGL7bGaayzFaaWaa0baaSqa
% aiaad6gacqGH9aqpcaaIXaaabaGaamOtaaaaaaa!3DF8!
\[
\left\{ {x_n } \right\}_{n = 1}^N
\]](../latex_cache/5960b3e63e93b0eadb7f05b6597dc081.png) . (The standard deviation
. (The standard deviation ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdmhaaa!37B0!
\[
\sigma
\]](../latex_cache/0bcead44095f85d706d5bd0d3ee69019.png) is known.) In the remainder of this question we will derive an iterative algorithm for finding values for
is known.) In the remainder of this question we will derive an iterative algorithm for finding values for ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacq
% aH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawUhacaGL9baaaaa!3AFA!
\[
{\left\{ {\mu _k } \right\}}
\]](../latex_cache/63181a36e52687072bbbd54c4488895f.png) that maximize the likelihood,
that maximize the likelihood,
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaWaaiWaaeaacaWG4bWaaSbaaSqaaiaad6gaaeqaaaGccaGL7bGa
% ayzFaaWaa0baaSqaaiaad6gacqGH9aqpcaaIXaaabaGaamOtaaaakm
% aaeeaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam4Aaaqabaaakiaa
% wUhacaGL9baacaGGSaGaeq4WdmhacaGLhWoaaiaawIcacaGLPaaacq
% GH9aqpdaqeqbqaaiaadcfadaqadaqaaiaadIhadaWgaaWcbaGaamOB
% aaqabaGcdaabbaqaamaacmaabaGaeqiVd02aaSbaaSqaaiaadUgaae
% qaaaGccaGL7bGaayzFaaGaaiilaiabeo8aZbGaay5bSdaacaGLOaGa
% ayzkaaaaleaacaWGUbaabeqdcqGHpis1aOGaaiOlaaaa!5BD3!
\[
P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \prod\limits_n {P\left( {x_n \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right)} .
\]](../latex_cache/e8f09972b3500b374a1e5b0fd19ae615.png)
Let L denote the natural log of the likelihood. Show that the derivative of the log likelihood with respect to ![Formula: \[{\mu _k }\]](../latex_cache/8e114e04047dfd2df6cd90fecc90cc9d.png) is given by
is given by
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
% GHciITaeaacqGHciITcqaH8oqBdaWgaaWcbaGaam4AaaqabaaaaOGa
% amitaiabg2da9maaqafabaGaamiCamaaBaaaleaacaWGRbGaaiiFai
% aad6gaaeqaaOWaaSaaaeaadaqadaqaaiaadIhadaWgaaWcbaGaamOB
% aaqabaGccqGHsislcqaH8oqBdaWgaaWcbaGaam4AaaqabaaakiaawI
% cacaGLPaaaaeaacqaHdpWCdaahaaWcbeqaaiaaikdaaaaaaOGaaiil
% aaWcbaGaamOBaaqab0GaeyyeIuoaaaa!4F8E!
\[
\frac{\partial }
{{\partial \mu _k }}L = \sum\limits_n {p_{k|n} \frac{{\left( {x_n - \mu _k } \right)}}
{{\sigma ^2 }},}
\]](../latex_cache/968180dae9f9ec36821998cd8cc198f2.png)
where ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
% aaleaacaWGRbGaaiiFaiaad6gaaeqaaOGaeyyyIORaamiuamaabmaa
% baGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaadUgadaabba
% qaaiaadIhadaWgaaWcbaGaamOBaaqabaGccaGGSaGaaCiUdaGaay5b
% SdaacaGLOaGaayzkaaaaaa!47DF!
\[
p_{k|n} \equiv P\left( {k_n = k\left| {x_n ,{\mathbf{\theta }}} \right.} \right)
\]](../latex_cache/1b5e0ed28e9818454709a25da45ef545.png) appeared above.
appeared above.
Derivation:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
% GHciITaeaacqGHciITcqaH8oqBdaWgaaWcbaGaam4AaaqabaaaaOGa
% ciiBaiaac6gacaWGqbWaaeWaaeaadaGadaqaaiaadIhadaWgaaWcba
% GaamOBaaqabaaakiaawUhacaGL9baadaqhaaWcbaGaamOBaiabg2da
% 9iaaigdaaeaacaWGobaaaOWaaqqaaeaadaGadaqaaiabeY7aTnaaBa
% aaleaacaWGRbaabeaaaOGaay5Eaiaaw2haaiaacYcacqaHdpWCaiaa
% wEa7aaGaayjkaiaawMcaaiabg2da9maalaaabaGaeyOaIylabaGaey
% OaIyRaeqiVd02aaSbaaSqaaiaadUgaaeqaaaaakmaaqafabaGaciiB
% aiaac6gacaWGqbWaaeWaaeaacaWG4bWaaSbaaSqaaiaad6gaaeqaaO
% WaaqqaaeaadaGadaqaaiabeY7aTnaaBaaaleaacaWGRbaabeaaaOGa
% ay5Eaiaaw2haaiaacYcacqaHdpWCaiaawEa7aaGaayjkaiaawMcaaa
% WcbaGaamOBaaqab0GaeyyeIuoaaaa!6A60!
\[
\frac{\partial }
{{\partial \mu _k }}\ln P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \frac{\partial }
{{\partial \mu _k }}\sum\limits_n {\ln P\left( {x_n \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right)}
\]](../latex_cache/d4fff688e4cb4a830395b148a0388ad0.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS
% aaaeaacqGHciITaeaacqGHciITcqaH8oqBdaWgaaWcbaGaam4Aaaqa
% baaaaOWaaabuaeaaciGGSbGaaiOBamaadmaabaWaaabuaeaacaWGWb
% WaaSbaaSqaaiaadUgaaeqaaOWaaSaaaeaacaaIXaaabaWaaOaaaeaa
% caaIYaGaeqiWdaNaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaqabaaaaO
% GaciyzaiaacIhacaGGWbWaamWaaeaacqGHsisldaWcaaqaamaabmaa
% baGaeqiVd02aaSbaaSqaaiaadUgaaeqaaOGaeyOeI0IaamiEamaaBa
% aaleaacaWGUbaabeaaaOGaayjkaiaawMcaamaaCaaaleqabaGaaGOm
% aaaaaOqaaiaaikdacqaHdpWCdaahaaWcbeqaaiaaikdaaaaaaaGcca
% GLBbGaayzxaaaaleaacaWGRbaabeqdcqGHris5aaGccaGLBbGaayzx
% aaaaleaacaWGUbaabeqdcqGHris5aaaa!6080!
\[
= \frac{\partial }
{{\partial \mu _k }}\sum\limits_n {\ln \left[ {\sum\limits_k {p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right]} } \right]}
\]](../latex_cache/86e7b4035c45e740407f4e2862f3fcca.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Zaaa
% buaeaadaWadaqaamaalaaabaGaamiCamaaBaaaleaacaWGRbaabeaa
% kmaalaaabaGaaGymaaqaamaakaaabaGaaGOmaiabec8aWjabeo8aZn
% aaCaaaleqabaGaaGOmaaaaaeqaaaaakmaalaaabaWaaeWaaeaacaWG
% 4bWaaSbaaSqaaiaad6gaaeqaaOGaeyOeI0IaeqiVd02aaSbaaSqaai
% aadUgaaeqaaaGccaGLOaGaayzkaaaabaGaeq4Wdm3aaWbaaSqabeaa
% caaIYaaaaaaakiGacwgacaGG4bGaaiiCamaadmaabaGaeyOeI0YaaS
% aaaeaadaqadaqaaiabeY7aTnaaBaaaleaacaWGRbaabeaakiabgkHi
% TiaadIhadaWgaaWcbaGaamOBaaqabaaakiaawIcacaGLPaaadaahaa
% WcbeqaaiaaikdaaaaakeaacaaIYaGaeq4Wdm3aaWbaaSqabeaacaaI
% YaaaaaaaaOGaay5waiaaw2faaaqaamaaqafabaGaamiCamaaBaaale
% aacaWGRbaabeaakmaalaaabaGaaGymaaqaamaakaaabaGaaGOmaiab
% ec8aWjabeo8aZnaaCaaaleqabaGaaGOmaaaaaeqaaaaakiGacwgaca
% GG4bGaaiiCamaadmaabaGaeyOeI0YaaSaaaeaadaqadaqaaiabeY7a
% TnaaBaaaleaacaWGRbaabeaakiabgkHiTiaadIhadaWgaaWcbaGaam
% OBaaqabaaakiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaakeaa
% caaIYaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaaaOGaay5waiaaw2
% faaaWcbaGaam4Aaaqab0GaeyyeIuoaaaaakiaawUfacaGLDbaaaSqa
% aiaad6gaaeqaniabggHiLdaaaa!7CFE!
\[
= \sum\limits_n {\left[ {\frac{{p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\frac{{\left( {x_n - \mu _k } \right)}}
{{\sigma ^2 }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right]}}
{{\sum\limits_k {p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right]} }}} \right]}
\]](../latex_cache/36d5d46d163b2f0805d07742b2476015.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaabuaeaaca
% WGWbWaaSbaaSqaaiaadUgaaeqaaOWaaSaaaeaacaaIXaaabaWaaOaa
% aeaacaaIYaGaeqiWdaNaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaqaba
% aaaOGaciyzaiaacIhacaGGWbWaamWaaeaacqGHsisldaWcaaqaamaa
% bmaabaGaeqiVd02aaSbaaSqaaiaadUgaaeqaaOGaeyOeI0IaamiEam
% aaBaaaleaacaWGUbaabeaaaOGaayjkaiaawMcaamaaCaaaleqabaGa
% aGOmaaaaaOqaaiaaikdacqaHdpWCdaahaaWcbeqaaiaaikdaaaaaaa
% GccaGLBbGaayzxaaaaleaacaWGRbaabeqdcqGHris5aOGaeyypa0Za
% aabuaeaacaWGqbWaaeWaaeaadaabcaqaaiaadIhadaWgaaWcbaGaam
% OBaaqabaaakiaawIa7aiaadUgadaWgaaWcbaGaamOBaaqabaGccqGH
% 9aqpcaWGPbGaaiilaiaahI7aaiaawIcacaGLPaaacaWGqbWaaeWaae
% aacaWGRbWaaSbaaSqaaiaad6gaaeqaaOGaeyypa0JaamyAaaGaayjk
% aiaawMcaaaWcbaGaamyAaaqab0GaeyyeIuoaaaa!6973!
\[
\sum\limits_k {p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right]} = \sum\limits_i {P\left( {\left. {x_n } \right|k_n = i,{\mathbf{\theta }}} \right)P\left( {k_n = i} \right)}
\]](../latex_cache/ac64de78a66933a927e697ce3399accb.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
% aaleaacaWGRbaabeaakmaalaaabaGaaGymaaqaamaakaaabaGaaGOm
% aiabec8aWjabeo8aZnaaCaaaleqabaGaaGOmaaaaaeqaaaaakiGacw
% gacaGG4bGaaiiCamaadmaabaGaeyOeI0YaaSaaaeaadaqadaqaaiab
% eY7aTnaaBaaaleaacaWGRbaabeaakiabgkHiTiaadIhadaWgaaWcba
% GaamOBaaqabaaakiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaa
% keaacaaIYaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaaaOGaay5wai
% aaw2faaiabg2da9iaadcfadaqadaqaaiaadUgadaWgaaWcbaGaamOB
% aaqabaGccqGH9aqpcaWGRbaacaGLOaGaayzkaaGaamiuamaabmaaba
% GaamiEamaaBaaaleaacaWGUbaabeaakmaaeeaabaGaam4AamaaBaaa
% leaacaWGUbaabeaakiabg2da9iaadUgacaGGSaGaaCiUdaGaay5bSd
% aacaGLOaGaayzkaaaaaa!6347!
\[
p_k \frac{1}
{{\sqrt {2\pi \sigma ^2 } }}\exp \left[ { - \frac{{\left( {\mu _k - x_n } \right)^2 }}
{{2\sigma ^2 }}} \right] = P\left( {k_n = k} \right)P\left( {x_n \left| {k_n = k,{\mathbf{\theta }}} \right.} \right)
\]](../latex_cache/e7fad6f8f95484fb7540dd2f4a2fc8fc.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H49aaS
% aaaeaacqGHciITaeaacqGHciITcqaH8oqBdaWgaaWcbaGaam4Aaaqa
% baaaaOGaciiBaiaac6gacaWGqbWaaeWaaeaadaGadaqaaiaadIhada
% WgaaWcbaGaamOBaaqabaaakiaawUhacaGL9baadaqhaaWcbaGaamOB
% aiabg2da9iaaigdaaeaacaWGobaaaOWaaqqaaeaadaGadaqaaiabeY
% 7aTnaaBaaaleaacaWGRbaabeaaaOGaay5Eaiaaw2haaiaacYcacqaH
% dpWCaiaawEa7aaGaayjkaiaawMcaaiabg2da9maaqafabaWaaSaaae
% aacaWGqbWaaeWaaeaacaWGRbWaaSbaaSqaaiaad6gaaeqaaOGaeyyp
% a0Jaam4AaaGaayjkaiaawMcaaiaadcfadaqadaqaaiaadIhadaWgaa
% WcbaGaamOBaaqabaGcdaabbaqaaiaadUgadaWgaaWcbaGaamOBaaqa
% baGccqGH9aqpcaWGRbGaaiilaiaahI7aaiaawEa7aaGaayjkaiaawM
% caaaqaamaaqafabaGaamiuamaabmaabaWaaqGaaeaacaWG4bWaaSba
% aSqaaiaad6gaaeqaaaGccaGLiWoacaWGRbWaaSbaaSqaaiaad6gaae
% qaaOGaeyypa0JaamyAaiaacYcacaWH4oaacaGLOaGaayzkaaGaamiu
% amaabmaabaGaam4AamaaBaaaleaacaWGUbaabeaakiabg2da9iaadM
% gaaiaawIcacaGLPaaaaSqaaiaadMgaaeqaniabggHiLdaaaaWcbaGa
% amOBaaqab0GaeyyeIuoakmaalaaabaWaaeWaaeaacaWG4bWaaSbaaS
% qaaiaad6gaaeqaaOGaeyOeI0IaeqiVd02aaSbaaSqaaiaadUgaaeqa
% aaGccaGLOaGaayzkaaaabaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaa
% aaaaa!89F6!
\[
\Rightarrow \frac{\partial }
{{\partial \mu _k }}\ln P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \sum\limits_n {\frac{{P\left( {k_n = k} \right)P\left( {x_n \left| {k_n = k,{\mathbf{\theta }}} \right.} \right)}}
{{\sum\limits_i {P\left( {\left. {x_n } \right|k_n = i,{\mathbf{\theta }}} \right)P\left( {k_n = i} \right)} }}} \frac{{\left( {x_n - \mu _k } \right)}}
{{\sigma ^2 }}
\]](../latex_cache/2c3b479a4f50f6a32f51e3e0e2c7c833.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Zaaa
% buaeaacaWGWbWaaSbaaSqaaiaadUgacaGG8bGaamOBaaqabaaabaGa
% amOBaaqab0GaeyyeIuoakmaalaaabaWaaeWaaeaacaWG4bWaaSbaaS
% qaaiaad6gaaeqaaOGaeyOeI0IaeqiVd02aaSbaaSqaaiaadUgaaeqa
% aaGccaGLOaGaayzkaaaabaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaa
% aaaaa!4840!
\[
= \sum\limits_n {p_{k|n} } \frac{{\left( {x_n - \mu _k } \right)}}
{{\sigma ^2 }}
\]](../latex_cache/c8011d7a11739ee0738f1c36b33e36ea.png)
Assuming that ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdmhaaa!37B0!
\[
\sigma
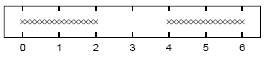
\]](../latex_cache/0bcead44095f85d706d5bd0d3ee69019.png) =1, sketch a contour plot of the likelihood function as a function of mu1 and mu2 for the data set shown above. The data set consists of 32 points. Describe the peaks in your sketch and indicate their widths.
=1, sketch a contour plot of the likelihood function as a function of mu1 and mu2 for the data set shown above. The data set consists of 32 points. Describe the peaks in your sketch and indicate their widths.
Solution:
We will be trying to plot the function
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
% aabaWaaiWaaeaacaWG4bWaaSbaaSqaaiaad6gaaeqaaaGccaGL7bGa
% ayzFaaWaa0baaSqaaiaad6gacqGH9aqpcaaIXaaabaGaamOtaaaakm
% aaeeaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam4Aaaqabaaakiaa
% wUhacaGL9baacaGGSaGaeq4WdmNaeyypa0JaaGymaaGaay5bSdaaca
% GLOaGaayzkaaaaaa!4B35!
\[
P\left( {\left\{ {x_n } \right\}_{n = 1}^32 \left| {\left\{ {\mu _k } \right\},\sigma = 1} \right.} \right)
\]](../latex_cache/71b40c661f5c9db63270e0e74a946f2e.png)
if we designate the function
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca
% aIXaaabaWaaOaaaeaacaaIYaGaeqiWdahaleqaaaaakiGacwgacaGG
% 4bGaaiiCamaabmaabaGaeyOeI0YaaSaaaeaadaqadaqaaiaadIhacq
% GHsislcqaH8oqBaiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaa
% keaacaaIYaaaaaGaayjkaiaawMcaaaaa!458F!
\[
{\frac{1}
{{\sqrt {2\pi } }}\exp \left( { - \frac{{\left( {x - \mu } \right)^2 }}
{2}} \right)}
\]](../latex_cache/2ad62d34e3684874733b4cb33953d5d3.png)
as p[x,mu] (remember that ![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdmhaaa!37B0!
\[
\sigma
\]](../latex_cache/0bcead44095f85d706d5bd0d3ee69019.png) =1 and
=1 and ![Formula: \[\frac{1}{{\sqrt {2\pi } }} = {\text{0}}{\text{.3989422804014327}}\]](../latex_cache/3007395e2c673cf6173195f8f616e34e.png) ),
),
![Formula: % MathType!MTEF!2!1!+-<br />
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb<br />
% WaaeWaaeaacaWG4bGaaiiFamaacmaabaGaeqiVd0gacaGL7bGaayzF<br />
% aaGaaiilaiabeo8aZbGaayjkaiaawMcaaiabg2da9maadmaabaWaaa<br />
% bCaeaadaqadaqaaiaadchadaWgaaWcbaGaam4AaaqabaGccqGH9aqp<br />
% caGGUaGaaGynaaGaayjkaiaawMcaamaalaaabaGaaGymaaqaamaaka<br />
% aabaGaaGOmaiabec8aWnaabmaabaGaeq4Wdm3aaWbaaSqabeaacaaI<br />
% YaaaaOGaeyypa0JaaGymamaaCaaaleqabaGaaGOmaaaaaOGaayjkai<br />
% aawMcaaaWcbeaaaaGcciGGLbGaaiiEaiaacchadaqadaqaaiabgkHi<br />
% TmaalaaabaWaaeWaaeaacaWG4bGaeyOeI0IaeqiVd02aaSbaaSqaai<br />
% aadUgaaeqaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaaGc<br />
% baGaaGOmaiabeo8aZnaaCaaaleqabaGaaGOmaaaaaaaakiaawIcaca<br />
% GLPaaaaSqaaiaadUgacqGH9aqpcaaIXaaabaGaaGOmaaqdcqGHris5<br />
% aaGccaGLBbGaayzxaaaabaGaeyypa0JaaiOlaiaaiwdadaqadaqaai<br />
% aahchadaWadaqaaiaadIhacaGGSaGaamyBaiaadwhacaaIXaaacaGL<br />
% BbGaayzxaaGaey4kaSIaaCiCamaadmaabaGaamiEaiaacYcacaWGTb<br />
% GaamyDaiaaikdaaiaawUfacaGLDbaaaiaawIcacaGLPaaacqGHHjIU<br />
% caWHWbGaaCiCamaadmaabaGaamiEaiaacYcacaWGTbGaamyDaiaaig<br />
% dacaGGSaGaamyBaiaadwhacaaIYaaacaGLBbGaayzxaaaaaaa!8AA0!<br />
\[<br />
\begin{gathered}<br />
P\left( {x|\left\{ \mu \right\},\sigma } \right) = \left[ {\sum\limits_{k = 1}^2 {\left( {p_k = .5} \right)\frac{1}<br />
{{\sqrt {2\pi \left( {\sigma ^2 = 1^2 } \right)} }}\exp \left( { - \frac{{\left( {x - \mu _k } \right)^2 }}<br />
{{2\sigma ^2 }}} \right)} } \right] \hfill \\<br />
= .5\left( {{\mathbf{p}}\left[ {x,mu1} \right] + {\mathbf{p}}\left[ {x,mu2} \right]} \right) \equiv {\mathbf{pp}}\left[ {x,mu1,mu2} \right] \hfill \\ <br />
\end{gathered} <br />
\]](../latex_cache/d8547ac7bb53e78258a1e9e9b6404ee4.png)
![Formula: % MathType!MTEF!2!1!+-<br />
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb<br />
% WaaeWaaeaadaGadaqaaiaadIhadaWgaaWcbaGaamOBaaqabaaakiaa<br />
% wUhacaGL9baadaqhaaWcbaGaamOBaiabg2da9iaaigdaaeaacaWGob<br />
% aaaOWaaqqaaeaadaGadaqaaiabeY7aTnaaBaaaleaacaWGRbaabeaa<br />
% aOGaay5Eaiaaw2haaiaacYcacqaHdpWCaiaawEa7aaGaayjkaiaawM<br />
% caaiabg2da9maarafabaGaamiuamaabmaabaGaamiEamaaBaaaleaa<br />
% caWGUbaabeaakmaaeeaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam<br />
% 4AaaqabaaakiaawUhacaGL9baacaGGSaGaeq4WdmhacaGLhWoaaiaa<br />
% wIcacaGLPaaaaSqaaiaad6gaaeqaniabg+GivdaakeaacqGH9aqpda<br />
% qeqbqaaiaahchacaWHWbWaamWaaeaacaWG4bGaaiilaiaad2gacaWG<br />
% 1bGaaGymaiaacYcacaWGTbGaamyDaiaaikdaaiaawUfacaGLDbaaaS<br />
% qaaiaad6gaaeqaniabg+GivdGccqGHHjIUcaWHWbGaaCiCaiaahcha<br />
% daWadaqaaiaadIhacaGGSaGaamyBaiaadwhacaaIXaGaaiilaiaad2<br />
% gacaWG1bGaaGOmaaGaay5waiaaw2faaaaaaa!791F!<br />
\[<br />
\begin{gathered}<br />
P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \prod\limits_n {P\left( {x_n \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right)} \hfill \\<br />
= \prod\limits_n {{\mathbf{pp}}\left[ {x,mu1,mu2} \right]} \equiv {\mathbf{ppp}}\left[ {x,mu1,mu2} \right] \hfill \\ <br />
\end{gathered} <br />
\]](../latex_cache/45d43b605033a4aa279f5db4b6c5f8cb.png)
then we have:
![Formula: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGqb<br />% WaaeWaaeaadaGadaqaaiaadIhadaWgaaWcbaGaamOBaaqabaaakiaa<br />% wUhacaGL9baadaqhaaWcbaGaamOBaiabg2da9iaaigdaaeaacaWGob<br />% aaaOWaaqqaaeaadaGadaqaaiabeY7aTnaaBaaaleaacaWGRbaabeaa<br />% aOGaay5Eaiaaw2haaiaacYcacqaHdpWCaiaawEa7aaGaayjkaiaawM<br />% caaiabg2da9maarafabaGaamiuamaabmaabaGaamiEamaaBaaaleaa<br />% caWGUbaabeaakmaaeeaabaWaaiWaaeaacqaH8oqBdaWgaaWcbaGaam<br />% 4AaaqabaaakiaawUhacaGL9baacaGGSaGaeq4WdmhacaGLhWoaaiaa<br />% wIcacaGLPaaaaSqaaiaad6gaaeqaniabg+GivdaakeaacqGH9aqpda<br />% qeqbqaaiaahchacaWHWbWaamWaaeaacaWG4bGaaiilaiaad2gacaWG<br />% 1bGaaGymaiaacYcacaWGTbGaamyDaiaaikdaaiaawUfacaGLDbaaaS<br />% qaaiaad6gaaeqaniabg+GivdGccqGHHjIUcaWHWbGaaCiCaiaahcha<br />% daWadaqaaiaadIhacaGGSaGaamyBaiaadwhacaaIXaGaaiilaiaad2<br />% gacaWG1bGaaGOmaaGaay5waiaaw2faaaaaaa!791F!<br />\[<br />\begin{gathered}<br /> P\left( {\left\{ {x_n } \right\}_{n = 1}^N \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right) = \prod\limits_n {P\left( {x_n \left| {\left\{ {\mu _k } \right\},\sigma } \right.} \right)} \hfill \\<br /> = \prod\limits_n {{\mathbf{pp}}\left[ {x,mu1,mu2} \right]} \equiv {\mathbf{ppp}}\left[ {x,mu1,mu2} \right] \hfill \\ <br />\end{gathered} <br />\]](../latex_cache/45d43b605033a4aa279f5db4b6c5f8cb.png)
And in Mathematica, these mean:
mx=Join[N[Range[0,2,2/15]],N[Range[4,6,2/15]]]
Length[mx]
ListPlot[Table[{mx[[i]],1},{i,1,32}]]
p[x_,mu_]:=0.3989422804014327` * Exp[-(mu-x)^2/2];
pp[x_,mu1_,mu2_]:=.5 (p[x,mu1]+p[x,mu2]);
ppp[xx_,mu1_,mu2_]:=Module[
{ptot=1},
For[i=1,i<=Length[xx],i++,
ppar = pp[xx[[i]],mu1,mu2];
ptot *= ppar;
(*Print[xx[[i]],"\t",ppar];*)
];
Return[ptot];
];
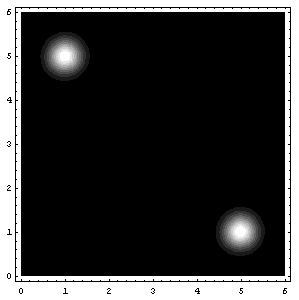
Plot3D[ppp[mx,mu1,mu2],{mu1,0,6},{mu2,0,6},PlotRange->{0,10^-25}];

ContourPlot[ppp[mx,mu1,mu2],{mu1,0,6},{mu2,0,6},{PlotRange->{0,10^-25},ContourLines->False,PlotPoints->250}];(*It may take a while with PlotPoints->250, so just begin with PlotPoints->25 *)
That’s all folks! (for today I guess 8) (and also, I know that I said next entry would be about the soft K-means two entries ago, but believe me, we’re coming to that, eventually 😉
Attachments: Mathematica notebook for this entry, MSWord Document (actually this one is intended for me, because in the future I may need them again)



Leave a Reply