Lewis “Powering the Planet” MRS Bulletin 32 808 2007
November 27, 2007 Posted by Emre S. Tasci
Powering the Planet / Nathan S. Lewis
MRS Bulletin 32 808 2007
(Recommended by Prof. Thijsse)
This article is an edited transcript based on the plenary presentation given by Nathan S. Lewis (California Institute of Technology) on April 11, 2007, at the Materials Research Society Spring Meeting in San Fransisco.
- Richard Smalley’s collaborator.
- The problem is not the extinction of fossil based fuels, they will be available for the future (roughly 50-150 years for oil / 200-600 years of natural gas / 2000 years of coal). "This does not even include the methane clathrates, off the continental shelves, which are estimated to exist in comparable quantities to all of the oil, coal and gas on our planet combined."
- The article focuses on the planet in the year 2050:
I chose 2050 for two reasons. First, achieving results in the energy industry is a much longer-term endeavor than, say, achieving results in the information technology business. In IT, for example, you can build a Web site and only a few years later become a Google. If you build a coalfired power plant, however, it will take about 40 years to pay itself off and deliver a reasonable return on investment. The energy infrastructure that we build in the next 10 years, therefore, is going to determine, by and large, what our planet’s energy mix is going to look like in 2050. The second reason for choosing 2050 is that today’s population wants to know what our planet’s energy picture is going to look like within a timeframe meaningful to them—the next 30 to 40 years.
- The real problem is the CO2 emission. If we stop emitting carbondioxide as of this moment, it will be about 350 ppm by 2050. Even 550 ppm rate looks pretty hard to obtain. "We do not know, except through climate models, what the implications of driving the atmospheric CO2 concentrations to any of these levels will be. There are about six major climate models, all differing from each other in detail."
- What can be done?
1 – Nuclear Power – Insufficient.
2 – Carbon sequestration – Very insufficient. "The U.S. department of Energy is doing work on carbon sequestration, with the goal of creating 1 gigaton of storage by 2025 and 4 gigatons total by 2050. Since the United State’s annual carbon emissions are 1.5 gigaton per year, the total DOE goal for 50 years from now is commensurate with a few years’ worth of current emissions.
3 – Renewable Carbon-Neutral Energy Sources – Highly insufficient. Not the time, nor the areas are available for this to work. But we should head to the sun. "To put that another way, more energy from the sun hits the earth in one hour than all of the energy consumed on our planet in an entire year." Also there is some debate about using geothermal energy but the the low temperature difference that will practically let us extract much less than a few terrawats sustainably over the 11.6 TW of sustainable global heat energy. - Solar cells / sun energy collectors must be cheaper about 1-10$/m2. Also the energy can not be stored efficiently. We can store it by pumping water uphill for example, but by comparison, we will need to pump 50000 gallons of water uphill for 100 m to replace 1 gallon of gasoline.
- Energy solutions for the future:
1 – Photovoltaics – Efficient but highly expensive.
2 – Semiconductor/Liquid Junctions – Promising.
3 – Photosynthesis – Must be researched for better efficiency. - Energy saving : "Any realistic energy program would start with energy efficiency, because saving energy costs much less than making energy. Because of all the inefficiencies in the energy supply chain, for every 1 J of energy that is saved at the end, 4-5 J is avoided from being produced."
- The problem is severe and critical and there isn’t much time to act:
Advocates of developing carbon-free energy alternatives believe that this is a project at which we cannot afford to fail because there is only one chance to get it right. For them, the question is whether or not, if the project went ahead, it could be completed in the time we have remaining. Because CO2 is extremely long-lived, there are not actually 50 years left to deal with the problem. To put this in perspective, consider the following comparisons. If we do not build the next "nano-widget," the world is going to stay the same overt he next 50 years – it will not be better, perhaps, but it will not be worse, either. Even if we do not develop a cure for cancer in 50 years, the world is going to stay basically the same, in spite of the tragedy caused by that disease. If we do not fix our energy problem within the next 20 years, however, we can, as scientists, say with absolute certainty that the world will simply not be the same, and that it will change in a way that, to our best knowledge, will affect life on our planet for the next 3000 years. What this cange will be, we do not precisely know. That is a risk management question. We simply know that no human will ever have experienced what we will within those 50 years, and the unmitigated results will last for a time scale comparable to modern human history.
If, on the other hand, we decided to do something about our energy problem, I am fairly optimistic we could succeed. As I have outlined, there are no new principles at play here. This challenge is not like trying to figure out how to build an atomic bomb, when we did not know the physics of bomb-building in the first place—which was the situation at the start of the Manhattan Project. We know how to build solar cells; they have a 30-year warranty. We have an existence proof with photosynthesis. We know the components of how to capture and store sunlight. We simply do not yet know how to make these processes cost-effective, over this scale.
Here, our funding priorities also come into the picture. In the United States, we spend $28 billion on health, but only about $28 million on basic solar research. Currently, we spend more money buying gas at the pump in one hour than we spend funding basic solar research in our country over an entire year. Yet, in that same hour, more energy from the sun is hitting the Earth than all of the energy consumed on our planet in that year. The same cannot be said of any other energy source. On the other hand, we need to explore all credible energy options that we believe could work at scale because we do not know which ones will work yet. In the end, we will need a mix of energy sources to meet the 10–20 TW demand, and we should be doing all we can to see that it works and works at scale, now and in the future. We have established that, as time goes on, we are going to require energy and we are going to require it in increasing amounts. I can say with confidence therefore, as Dr. Smalley did, that energy is the biggest scientific and technological problem facing our planet in the next 50 years.
Bayesian Inference – An introduction with an example
November 26, 2007 Posted by Emre S. Tasci
Suppose that Jo (of Example 2.3 in MacKay’s previously mentioned book), decided to take a test to see whether she’s pregnant or not. She applies a test that is 95% reliable, that is if she’s indeed pregnant, than there is a 5% chance that the test will result otherwise and if she’s indeed NOT pregnant, the test will tell her that she’s pregnant again by a 5% chance (The other two options are test concluding as positive on pregnancy when she’s indeed pregnant by 95% of all the time, and test reports negative on pregnancy when she’s actually not pregnant by again 95% of all the time). Suppose that she is applying contraceptive drug with a 1% fail ratio.
Now comes the question: Jo takes the test and the test says that she’s pregnant. Now what is the probability that she’s indeed pregnant?
I would definitely not write down this example if the answer was 95% percent as you may or may not have guessed but, it really is tempting to guess the probability as 95% the first time.
The solution (as given in the aforementioned book) is:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaabbeaacaWGqb
% GaaiikaiaadshacaWGLbGaam4CaiaadshacaGG6aGaaGymaiaacYha
% caWGWbGaamOCaiaadwgacaWGNbGaaiOoaiaaigdacaGGPaGaeyypa0
% ZaaSaaaeaacaWGqbGaaiikaiaadchacaWGYbGaamyzaiaadEgacaGG
% 6aGaaGymaiaacYhacaWG0bGaamyzaiaadohacaWG0bGaaiOoaiaaig
% dacaGGPaGaamiuaiaacIcacaWGWbGaamOCaiaadwgacaWGNbGaaiOo
% aiaaigdacaGGPaaabaGaamiuaiaacIcacaWG0bGaamyzaiaadohaca
% WG0bGaaiOoaiaaigdacaGGPaaaaaqaaiabg2da9maalaaabaGaamiu
% aiaacIcacaWGWbGaamOCaiaadwgacaWGNbGaaiOoaiaaigdacaGG8b
% GaamiDaiaadwgacaWGZbGaamiDaiaacQdacaaIXaGaaiykaiaadcfa
% caGGOaGaamiCaiaadkhacaWGLbGaam4zaiaacQdacaaIXaGaaiykaa
% qaamaaqafabaGaamiuaiaacIcacaWG0bGaamyzaiaadohacaWG0bGa
% aiOoaiaaigdacaGG8bGaamiCaiaadkhacaWGLbGaam4zaiaacQdaca
% WGPbGaaiykaiaadcfacaGGOaGaamiCaiaadkhacaWGLbGaam4zaiaa
% cQdacaWGPbGaaiykaaWcbaGaamyAaaqab0GaeyyeIuoaaaaakeaacq
% GH9aqpdaWcaaqaaiaaicdacaGGUaGaaGyoaiaaiwdacqGHxdaTcaaI
% WaGaaiOlaiaaicdacaaIXaaabaGaaGimaiaac6cacaaI5aGaaGynai
% abgEna0kaaicdacaGGUaGaaGimaiaaigdacqGHRaWkcaaIWaGaaiOl
% aiaaicdacaaI1aGaey41aqRaaGimaiaac6cacaaI5aGaaGyoaaaaae
% aacqGH9aqpcaaIWaGaaiOlaiaaigdacaaI2aaaaaa!ADD3!
\[
\begin{gathered}
P(test:1|preg:1) = \frac{{P(preg:1|test:1)P(preg:1)}}
{{P(test:1)}} \\
= \frac{{P(preg:1|test:1)P(preg:1)}}
{{\sum\limits_i {P(test:1|preg:i)P(preg:i)} }} \\
= \frac{{0.95 \times 0.01}}
{{0.95 \times 0.01 + 0.05 \times 0.99}} \\
= 0.16 \\
\end{gathered}
\]](../latex_cache/6453cf859b172f767097226e22e99927.png)
where P(b:bj|a:ai) represents the probability of b having the value bj given that a=ai. So Jo has P(test:1|preg=1) = 16% meaning that given that Jo is actually pregnant, the test would give the positive result by a probability of 16%. So we took into account both the test’s and the contra-ceptive’s reliabilities. If this doesn’t make sense and you still want to stick with the somehow more logical looking 95%, think the same example but this time starring John, Jo’s humorous boyfriend who as a joke applied the test and came with a positive result on pregnancy. Now, do you still say that John is 95% pregnant? I guess not Just plug in 0 for P(preg:1) to the equation above and enjoy the outcoming likelihood of John being non-pregnant equaling to 0…
The thing to keep in mind is the probability of a being some value ai when b is bj is not equal to the probability of b being bj when a is equal to ai.
(7,4) Hamming Code
November 23, 2007 Posted by Emre S. Tasci
The (7,4) Hamming Code is a system that is used for sending bits of block length 4 (16 symbols) with redundancy resulting in transmission of blocks of 7 bits length. The first 4 bits of the transmitted information contains the original source bits and the last three contains the parity-check bits for {1,2,3}, {2,3,4} and {1,3,4} bits.
It has a transmission rate of 4/7 ~ 0.57 . Designate the source block as s, the transmission operator as G so that transmitted block t is t = GTs and parity check operator is designated as H where:
![Formula: % MathType!MTEF!2!1!+-<br> % feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br> % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br> % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br> % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br> % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCisaiabg2<br> % da9maadmaabaqbaeaGboWbaaaabaGaaGymaaqaaiaaigdaaeaacaaI<br> % XaaabaGaaGimaaqaaiaaigdaaeaacaaIWaaabaGaaGimaaqaaiaaic<br> % daaeaacaaIXaaabaGaaGymaaqaaiaaigdaaeaacaaIWaaabaGaaGym<br> % aaqaaiaaicdaaeaacaaIXaaabaGaaGimaaqaaiaaigdaaeaacaaIXa<br> % aabaGaaGimaaqaaiaaicdaaeaacaaIXaaaaaGaay5waiaaw2faaaaa<br> % !4A2B!<br> ${\bf{H}} = \left[ {\begin{array}{*{20}c}<br> 1 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\<br> 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\<br> 1 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\<br> \end{array}} \right]$<br>](../latex_cache/4588c14c4af56a662e011f912cd8a4b7.png)
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCiuaiabg2
% da9maadmaabaqbaeaGboabaaaabaGaaGymaaqaaiaaigdaaeaacaaI
% XaaabaGaaGimaaqaaiaaicdaaeaacaaIXaaabaGaaGymaaqaaiaaig
% daaeaacaaIXaaabaGaaGimaaqaaiaaigdaaeaacaaIXaaaaaGaay5w
% aiaaw2faaaaa!4399!
\[
{\mathbf{P}} = \left[ {\begin{array}{*{20}c}
1 \hfill & 1 \hfill & 1 \hfill & 0 \hfill \\
0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\
1 \hfill & 0 \hfill & 1 \hfill & 1 \hfill \\
\end{array} } \right]
\]](../latex_cache/672a07f960375e53a05a3340ef147c53.png)
As it calculates the parities for bits, also its Modulo wrt 2 must be included. Since we’re calculating the parities for {1,2,3}, {2,3,4} and {1,3,4} bit-groups, the values of the P are easily understandable. Now, we will join the Identity Matrix of order 4 (for directly copying the first 4 values) with the P operator to construct the GT transformation (encoder) operator:
![Formula: % MathType!MTEF!2!1!+-
% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaC4ramaaCa
% aaleqabaGaamivaaaakiabg2da9maadmaabaqbaeaGbEabaaaaaeaa
% caaIXaaabaGaaGimaaqaaiaaicdaaeaacaaIWaaabaGaaGOmaaqaai
% aaigdaaeaacaaIWaaabaGaaGimaaqaaiaaicdaaeaacaaIWaaabaGa
% aGymaaqaaiaaicdaaeaacaaIWaaabaGaaGimaaqaaiaaicdaaeaaca
% aIXaaabaGaaGymaaqaaiaaigdaaeaacaaIXaaabaGaaGimaaqaaiaa
% icdaaeaacaaIXaaabaGaaGymaaqaaiaaigdaaeaacaaIXaaabaGaaG
% imaaqaaiaaigdaaeaacaaIXaaaaaGaay5waiaaw2faaaaa!505A!
\[
{\mathbf{G}}^T = \left[ {\begin{array}{*{20}c}
1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\
0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\
0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\
0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\
1 \hfill & 1 \hfill & 1 \hfill & 0 \hfill \\
0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\
1 \hfill & 0 \hfill & 1 \hfill & 1 \hfill \\
\end{array} } \right]
\]](../latex_cache/faa48ff3c983ec75ba4a7260fa7609dc.png)
and H is actually nothing but [-P I3]. It can be seen that HGTs will always result {0,0,0} in a parity check, meaning that all three parities have passed the test. So, where is the problem?
Noise: Noise is the operator that flips the values of bits randomly with an occuring probability f. Suppose that we have a source signal block of 4 bits length: {s1, s2, s3, s4}. I encode this information with calculating the parities and adding them to the end, thus coming up with a block of 7 bits length and call this block as t (for transmitted):
t=GTs (supposing t and s are given as column vectors. Otherwise, t=sG)
Now I send this packet but on the road to the receiver, the noise changes it and so, the received message, r, is the transmitted message (t) AND the noise (n):
r=t+s
Since I have got the parity information part (which may also have been affected by the noise), I compare the received data’s first 4 values with the parity information stored in the last 3 values. A very practical way of doing this is using 3 intersecting circles and placing them as:
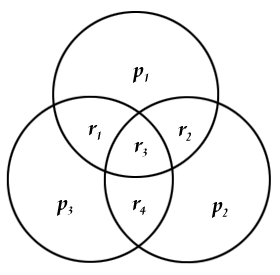
with r1-r4 representing the first values (ie, actual data) received and p1-p3 being the parity information (the last 3 values). So we place the values to their corresponding locations and easily can check if the parity matches to the related values. We can have 8 different situations at this moment. Let’s denote the z=Hr vector as the parity check result. z={0,0,0} if all three parity information agrees with the calculated ones, z={1,0,0} if only p1 is different from the calculated parity of {r1,r2,r3}, z={1,0,1} if p1 AND p3 are different from their corresponding calculated parities and so on. If there is only 1 error (ie, only one "1" and two "0") in the parity check, then it means that, the noise affected only the parity information, not the data encoded (ie, the first 4 values), so the corrupted data can be fixed by simply switching the faulty parity. If there are 2 parity check errors, this time, the value on the intersection of the corresponding parities (ie, r1 for p1&p3, r2 for p1&p2 and r4 for p2&p3,) must be switched. If z={1,1,1} then r3 should be switched.
Let’s introduce some mathematica operations and then tackle with some examples. You can just copy and paste them since there are no additional libraries required:
mGT = {{1,0,0,0},{0,1,0,0},{0,0,1,0},{0,0,0,1},{1,1,1,0},{0,1,1,1},{1,0,1,1}};
mH = {{1,1,1,0,1,0,0},{0,1,1,1,0,1,0},{1,0,1,1,0,0,1}};
(mS = {{1},{1},{1},{0}});
Mod[(mGTS=mGT . mS),2] // MatrixForm
mN ={0,0,0,0,0,0,1};
(mR = Mod[mGTS+mN,2]) // MatrixForm
mZ = Mod[mH . mR,2];
Flatten[mZ]
The first two lines define GT and H and from here, you can check a very important property being:
Mod[mH.mGT,2] // MatrixForm
equal to 0.
We introduce the 4bit data to be transmitted as mS which we had referred as s through out the text. Then we encode the data to be send with the parity info encoded as mGTS (t) add a noise mN (n) to it assuming it is corrupted in the transmission process and the data the other side receives is mR (r) consisting of the data transmitted AND the noise acted on it. mZ is the parity check result (z) (I’ve "Flatten"ed it for a better view). In the operations above, the "Mod" operator is frequently used because of our universe being a mod2 universe (2=0, 3=1, 4=0,… just 0s and 1s actually!).
So, in this example, we had s={1,1,1,0}, and this was encoded as t={1,1,1,0,1,0,0} and on its way to the happy-ending, a noise corrupted it and switched its 3rd parity information from 0 to 1. As a result of this, the recipient got its data as r={1,1,1,0,1,0,1}. But since our recipient is not that dull, a parity check is immediately applied and it was seen that z={0,0,1} meaning that, there is something wrong with the 3rd parity information, and nothing wrong with the information received at all!
Now, let’s apply all the possible noises given that only one value can be switched at a time (ie, only one 1 in the n vector with the remaining all being 0s).
For[i = 1, i <= 7, i++,
mN = {0, 0, 0, 0, 0, 0, 0} ;
mN = ReplacePart[mN, 1, i];
mR = Mod[mGTS + mN, 2];
mZ = Mod[mH . mR, 2];
Print[mN, "\t", Flatten[mZ]];
];
After this, if everything went right, you’ll see the output something like this:
{1,0,0,0,0,0,0} {1,0,1}
{0,1,0,0,0,0,0} {1,1,0}
{0,0,1,0,0,0,0} {1,1,1}
{0,0,0,1,0,0,0} {0,1,1}
{0,0,0,0,1,0,0} {1,0,0}
{0,0,0,0,0,1,0} {0,1,0}
{0,0,0,0,0,0,1} {0,0,1}
So we know exactly what went wrong at are able to correct it… Everything seems so perfect, so there must be a catch…
There is no decoding error as long as there is only 1 corruption per data block!
As the corruption number increases, there is no way of achieving the original data send with precise accuracy. Suppose that we re-send our previous signal s={1,1,1,0} which yields t={1,1,1,0,1,0,0} but this time the noise associated with the signal is n={0,1,0,0,0,0,1} so, the received signal is r={1,0,1,0,1,0,1}. When we apply the partition check, we have z={1,1,1}, which means that, there is a problem with the 3rd value and we deduce that the original message transmitted was t={1,0,0,0,1,0,1} which passes the parity check tests with success alas a wrongly decoded signal!
The probability of block error, pB is the probability that there will at least be one decoded bit that will not match the transmitted bit. A little attention must be paid about this statement. It emphasizes the decoded bit part, not the received bit. So, in our case of (4,7) Hamming Code, there won’t be a block error as long as there is only one corrupted bit in the received bit because we are able to construct the transmitted bits with certainty in that case. Only if we have two or more bits corrupted, we won’t be able to revive the original signal, so, pB scales as O(f2).
References : I have heavily benefitted from David MacKay’s resourceful book Information Theory, Inference, and Learning Algorithms which is available for free for viewing on screen.
|
A Crash Course on Information Gain & some other DataMining terms and How To Get There
November 21, 2007 Posted by Emre S. Tasci
Suppose that you have -let’s say- 5 pipelines outputting Boolean values seemingly randomly such as:

Now, we will be looking for a possible relation between these variables -let’s name that {a,b,c,d,e}� (Suppose that we do not know that the first 3 variables (a,b,c)� are randomly tossed, while the 4th (d)� is just “a AND b” and the 5th one (e) is actually “NOT a”).
- We look for different possible values of each variable and store them in an array called posVals (as obvius, from “Possible Values”). In our example, each of the variables can have only two values, so our posVals array will look something like this:

- Now that we know the possible outcomes for each of the variables, we calculate the probability of each of these values by simply counting them and then dividing to the total number of output. As an example, for the 3rd variable,� there are four 0’s and 6 1’s totaling 10 values. So, the probability of a chosen value to be 0 would be 4 out of 10 and 6/10 for 1. We store the probabilities in an array called probs this time which is like
�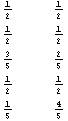
In the� 3rd row, the probabilities for the c variable are stored in the order presented in the posVals array (check the 3rd row of posVals to see that the first value is 1 and the second is 0). You can object the unnecessity of storing the second row of probs because, the second row is always equal to 1-probs[[1]] (I will be using the Mathematica notation for array elements, with a[[1]] meaning the 1st row if a is a matrix, or 1st element if a is a 1-D List; a[[1]][[3]] meaning the element on the first row and third column of the matrix a), but it is only a specific case that we are dealing with Boolean outputs. Yes,� a variable’s probability always equals to the sum of the probabilities of all the other variables subtracted from 1 but we will keep record of all the probabilities for practical reasons. - Now we will calculate the entropy for each variable. Entropy is a measure of order in a distribution and a higher entropy corresponds to a more disordered system. For our means, we will calculate the entropy as
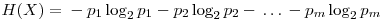
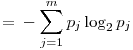
In these formulas, H represents the entropy, represents the probability of the jth value for variable X. Let’s store this values in the entropies array.
represents the probability of the jth value for variable X. Let’s store this values in the entropies array. - Special Conditional Entropy,
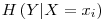 � is defined as the entropy of the Y variable values for which the corresponding X variable values equal to
� is defined as the entropy of the Y variable values for which the corresponding X variable values equal to 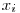 .� For� our given example, let’s calculate H(d|a=1): Searching through the data, we see that, a=1 for rows: {1,3,4,7,10} and the values of d in these rows correspond to: {1,0,0,0,1}. Let’s assume this set ({1,0,0,0,1}) as a brand new set and go on from here.� Applying the definition of the entropy given in the 3rd step, we have:
.� For� our given example, let’s calculate H(d|a=1): Searching through the data, we see that, a=1 for rows: {1,3,4,7,10} and the values of d in these rows correspond to: {1,0,0,0,1}. Let’s assume this set ({1,0,0,0,1}) as a brand new set and go on from here.� Applying the definition of the entropy given in the 3rd step, we have:
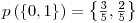
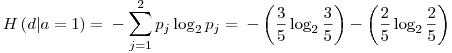
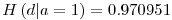
- Conditional Entropy,
 is the entropy including all the possible values of the variable being tested (X)� as having a relation to the� targeted� variable (Y). It is calculated as:
is the entropy including all the possible values of the variable being tested (X)� as having a relation to the� targeted� variable (Y). It is calculated as:
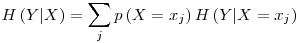
Again, if we look at our example, since we have H(d|a=1) =� 0.970951, p(a=1) = 0.5 ; and if we calculate H(d|a=0) in a similar way as in step 4, we find H(d|a=0) = 0 and taking
we find that H(d|a) = 0.5 x 0.970951 + 0.5 x 0 = 0.4854755 - Information Gain,
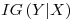 – is a measure of the effect a variable (X)� is having against� a targetted variable (Y) with the information on the entropy of the targetted variable itself (H(Y))� taken into account. It is calculated as:
– is a measure of the effect a variable (X)� is having against� a targetted variable (Y) with the information on the entropy of the targetted variable itself (H(Y))� taken into account. It is calculated as:

For our example , H(d) = 0.721928 and we calculated H(d|a=0) = 0.4854755 so, IG(d|a) = 0.236453. Summing up, for the data (of 10 for each variable)� presented in step 1, we have the Information Gain Table as:
| X |
IG(e|X) |
X |
IG(d|X) |
X |
IG(c|X) |
| a |
1.0 |
a |
0.236453 |
a |
0.124511 |
| b |
0.0290494 |
b |
0.236453 |
b |
0.0 |
| c |
0.124511 |
c |
0.00740339 |
d |
0.00740339 |
| d |
0.236453 |
e |
0.236453 |
e |
0.124511 |
| X |
IG(b|X) |
X |
IG(a|X) |
| a |
0.0290494 |
b |
0.0290494 |
| c |
0.0 |
c |
0.124511 |
| d |
0.236453 |
d |
0.236453 |
| e |
0.0290494 |
e |
1.0 |
And here are the results for 1000 values per variable instead of 10:
| X |
IG(e|X) |
X |
IG(d|X) |
X |
IG(c|X) |
| a |
0.996257 |
a |
0.327922 |
a |
0.000500799 |
| b |
0.000716169 |
b |
0.29628 |
b |
0.00224924 |
| c |
0.000500799 |
c |
0.000982332 |
d |
0.000982332 |
| d |
0.327922 |
e |
0.327922 |
e |
0.000500799 |
| X |
IG(b|X) |
X |
IG(a|X) |
| a |
0.000716169 |
b |
0.000716169 |
| c |
0.00224924 |
c |
0.000500799 |
| d |
0.29628 |
d |
0.327922 |
| e |
0.000716169 |
e |
0.996257 |
What can we say about the relationships from these Information Gain results?
- H(Y|X) = H(X|Y) – Is this valid for this specific case or is it valid for� general?
- Variable a: We can most probably guess a if we had known e, and it is somehow correlated with d.
- Variable b: It is correlated with d.
- Variable c: There doesn’t seem to be any correlation.
- Variable d: It is equally correlated with a&e and also correlated with b very closely to that correlation with a&e.
- Variable e: It is VERY strongly correlated with a and� it is somehow correlated with d.
Let’s take it on from here, with the variable d:
This is the IG table for 10000 data per each variable:
| X |
IG(d|X) |
| a |
0.30458 |
| b |
0.297394 |
| c |
0.00014876 |
| e |
0.30458 |
This is the IG table for 100000 data per each variable:
| X |
IG(d|X) |
| a |
0.309947 |
| b |
0.309937 |
| c |
1.97347×10^-6 |
| e |
0.309947 |
You can download the Mathematica sheet for this example : Information Gain Example
You will also need the two libraries (Matrix & DataMining) to run the example.
Mathematica Matrix Examples
November 19, 2007 Posted by Emre S. Tasci
Mathematica Matrix Manipulation Examples
B={Range[5],Range[6,10],Range[11,15],Range[16,20]} ;
TableForm[B]
(* To extract rows 2 & 3 *)
Part[B,{2,3}] // TableForm
(* To extract cols 2 & 4 *)
Part[B, All,{2,4}] // TableForm
(* To extract the intersection of Rows 2&3 with Cols 2&4 *)
Part[B,{2,3} ,{2,4}] // TableForm
(* Selecting the values from the 2. row where B[[4]][[i]] has a specific value like <10 *)
Select[B[[2]],#<10&]
(* Selecting the values from the 2. col where B[[i]][[2]] has a specific value like <10 *)Select[Part[B,All,2],#<10&]
(* Alternative Transpose (//Equivalent to Transpose[matrixIN]//)*)
TransposeEST[matrixIN_]:=Module[
{matrixOUT},
numCols = Dimensions[matrixIN][[2]];
matrixOUT = Array[mo,numCols];
For[i=1,i<=numCols,i++,
� � � matrixOUT[[i]]=Part[matrixIN,All,i];
]
TableForm[matrixOUT];
Return[matrixOUT];
]
(* Swapping two rows *)
({B[[2]],B[[4]]}={B[[4]],B[[2]]}) // TableForm
(*Reading data from a file with a content like this:
0.642864000 0.761961000 1.665420000
5.815150000 3.603020000 1.831920000
6.409050000 7.150810000 0.966674000
5.389080000 4.989350000 6.571080000
6.044070000 4.887170000 7.005700000
6.806280000 2.766540000 4.030720000
6.676540000 0.652834000 5.729050000
1.231490000 5.754580000 0.404114000
9.722660000 7.571420000 1.133980000
8.869320000 7.574570000 4.886290000
1.221750000 8.511380000 6.201370000
2.817450000 0.216682000 6.474590000
5.638430000 7.422500000 7.381840000
8.903770000 4.192770000 0.355182000
7.073810000 1.421990000 1.606240000
7.646660000 1.979770000 3.877830000
8.239190000 1.280060000 6.705840000
4.430740000 2.016050000 5.515660000
9.771000000 2.637290000 8.423900000
8.916410000 4.900040000 2.592560000
*)
m=OpenRead["d:\lol1.txt"];
k= ReadList[m,Number];
Close[m];
(k =Partition[k,3]) // TableForm
(* And you can definitely Plot it too *)
<<Graphics`Graphics3D`
ScatterPlot3D[k,PlotStyle®{{PointSize[0.04],GrayLevel[0.09]}}]



