The marriage of heaven (common elements) and hell (code writing code).
June 26, 2008 Posted by Emre S. Tasci
So, as Blake had said, "Energy is Eternal Delight." or in other words, let’s merge the preceding two entries to write a code for a function that produces MySQL queries that will fetch the common elements involved with the given elements:
function fetch_elements($el,$order,$total)
{
// produces the query to select the elements that have binaries with the $el
// $order and $total are used to adjust the tab positions and designating the sets
$abc = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
$tab = str_repeat("\t",($total-$order));
$lom = <<<LOM
$tab SELECT symbol_A AS symb, val1 AS val$abc[$order]
$tab FROM `dbl014`
$tab WHERE symbol_B = "$el"
$tab GROUP BY Symbol_A
$tab UNION
$tab SELECT symbol_B AS symb, val1 AS val$abc[$order]
$tab FROM `dbl014`
$tab WHERE (
$tab symbol_A = "$el"
$tab AND symbol_B != ""
$tab )
$tab GROUP BY Symbol_B
LOM;
return $lom;
}
function merge_queries($str1,$str2,$or1,$or2,$tab)
{
// merges two node (or node group) queries (formed via fetch_elements() function)
// using the INNER JOIN function
return "$tab SELECT *\n$tab FROM (\n".$str1."\n$tab ) AS $or1\n$tab INNER JOIN (\n".$str2."\n$tab ) AS $or2\n$tab USING (symb)\n$tab ";
}
function fetch_common_elements($ar_el)
{
// produces the query that selects the common elements that have binaries with all of the elements given in the $ar_el array (using their symbols)
$total = sizeof($ar_el);
$abc = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
//$tab = str_repeat("\t",($total-$order-1));
$str[0] = fetch_elements($ar_el[0],0,$total-1);
$str[1] = fetch_elements($ar_el[1],1,$total);
$stri = merge_queries($str[0],$str[1],"A","B",str_repeat("\t",($total-2)));
for($i=2;$i<$total;$i++)
{
$str[$i] = fetch_elements($ar_el[$i],$i,$total);
$stri = merge_queries($str[$i],$stri,$abc[$i],$abc[($i+1)],str_repeat("\t",($total-$i-1)));
}
return $stri;
}
Now, we can call it with, for example:
echo fetch_common_elements(Array("Ga","Fe","Gd","Y","Ti","Ge","Ce"));
Which will output:
SELECT *
FROM (
SELECT symbol_A AS symb, val1 AS valG
FROM `dbl014`
WHERE symbol_B = "Ce"
GROUP BY Symbol_A
UNION
SELECT symbol_B AS symb, val1 AS valG
FROM `dbl014`
WHERE (
symbol_A = "Ce"
AND symbol_B != ""
)
GROUP BY Symbol_B
) AS G
INNER JOIN (
SELECT *
FROM (
SELECT symbol_A AS symb, val1 AS valF
FROM `dbl014`
WHERE symbol_B = "Ge"
GROUP BY Symbol_A
UNION
SELECT symbol_B AS symb, val1 AS valF
FROM `dbl014`
WHERE (
symbol_A = "Ge"
AND symbol_B != ""
)
GROUP BY Symbol_B
) AS F
INNER JOIN (
SELECT *
FROM (
SELECT symbol_A AS symb, val1 AS valE
FROM `dbl014`
WHERE symbol_B = "Ti"
GROUP BY Symbol_A
UNION
SELECT symbol_B AS symb, val1 AS valE
FROM `dbl014`
WHERE (
symbol_A = "Ti"
AND symbol_B != ""
)
GROUP BY Symbol_B
) AS E
INNER JOIN (
SELECT *
FROM (
SELECT symbol_A AS symb, val1 AS valD
FROM `dbl014`
WHERE symbol_B = "Y"
GROUP BY Symbol_A
UNION
SELECT symbol_B AS symb, val1 AS valD
FROM `dbl014`
WHERE (
symbol_A = "Y"
AND symbol_B != ""
)
GROUP BY Symbol_B
) AS D
INNER JOIN (
SELECT *
FROM (
SELECT symbol_A AS symb, val1 AS valC
FROM `dbl014`
WHERE symbol_B = "Gd"
GROUP BY Symbol_A
UNION
SELECT symbol_B AS symb, val1 AS valC
FROM `dbl014`
WHERE (
symbol_A = "Gd"
AND symbol_B != ""
)
GROUP BY Symbol_B
) AS C
INNER JOIN (
SELECT *
FROM (
SELECT symbol_A AS symb, val1 AS valA
FROM `dbl014`
WHERE symbol_B = "Ga"
GROUP BY Symbol_A
UNION
SELECT symbol_B AS symb, val1 AS valA
FROM `dbl014`
WHERE (
symbol_A = "Ga"
AND symbol_B != ""
)
GROUP BY Symbol_B
) AS A
INNER JOIN (
SELECT symbol_A AS symb, val1 AS valB
FROM `dbl014`
WHERE symbol_B = "Fe"
GROUP BY Symbol_A
UNION
SELECT symbol_B AS symb, val1 AS valB
FROM `dbl014`
WHERE (
symbol_A = "Fe"
AND symbol_B != ""
)
GROUP BY Symbol_B
) AS B
USING (symb)
) AS D
USING (symb)
) AS E
USING (symb)
) AS F
USING (symb)
) AS G
USING (symb)
) AS H
USING (symb)
and when fed to the database will yield:

thank y’all.. 8)
(Un)Common?
June 24, 2008 Posted by Emre S. Tasci
They say that, it is the opposite (unsimilar) couples that make up for much stabler relationships… If you have only 2 different values, (+) and (-), spin up and down, man and woman, then the unsimilar of a thing that is unsimilar to you equals to a thing that is similar to you. Although it is generally not valid for elements, it gives you an insight nonetheless.. So if Y, Gd, Fe and Ga play a similar part in dearest ZrO2‘s life, let’s check for their other common "partners" that are known to have some connection/involvement this or that way…
The table we’re interested in today holds the formula and the constituent elements as in the example below:
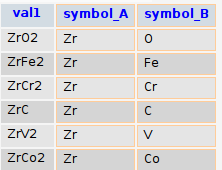
(Actually the table contains way more properties than the formula and the constituent elements but I’ve focused only to the relevant props)
symbol_A and symbol_B are position oriented wrt the written formula, meaning that for an AxBy binary, you have A for symbol_A and B for symbol_B whereas if it is BxAy, then they are reversed.
We will be looking for elements that form binaries with the aforementioned 4 elements, namely: Yttrium, Gadolinium, Iron and Gallium.
We can search for each of these 4 via the following query and then add it up:
SELECT symbol_A as symb,val1 FROM `dbl014`
WHERE symbol_B="Gd"
GROUP BY Symbol_A
UNION
SELECT symbol_B as symb, val1 FROM `dbl014`
WHERE (symbol_A="Gd" AND symbol_B!="")
GROUP BY Symbol_B
For the intersection of two elements, we glue the two like the above one via the INNER JOIN function:
SELECT * FROM
(
SELECT symbol_A as symb,val1
FROM `dbl014`
WHERE symbol_B="Gd"
GROUP BY Symbol_A
UNION
SELECT symbol_B as symb, val1
FROM `dbl014` WHERE (symbol_A="Gd" AND symbol_B!="")
GROUP BY Symbol_B
) AS A
INNER JOIN
(
SELECT symbol_A as symb,val1
FROM `dbl014` WHERE symbol_B="Y"
GROUP BY Symbol_A
UNION
SELECT symbol_B as symb, val1
FROM `dbl014` where (symbol_A="Y" AND symbol_B!="")
GROUP BY Symbol_B
) AS B
USING (symb)
ORDER BY symb
And for the ultimate quattro, it gets even exciting! :
SELECT *
FROM (
SELECT symbol_A AS symb, val1 AS val
FROM `dbl014`
WHERE symbol_B = "Fe"
GROUP BY Symbol_A
UNION
SELECT symbol_B AS symb, val1 AS val
FROM `dbl014`
WHERE (
symbol_A = "Fe"
AND symbol_B != ""
)
GROUP BY Symbol_B
) AS A
INNER JOIN (
SELECT *
FROM (
SELECT symbol_A AS symb, val1 AS valA
FROM `dbl014`
WHERE symbol_B = "Gd"
GROUP BY Symbol_A
UNION
SELECT symbol_B AS symb, val1 AS valA
FROM `dbl014`
WHERE (
symbol_A = "Gd"
AND symbol_B != ""
)
GROUP BY Symbol_B
) AS A
INNER JOIN (
SELECT *
FROM (
SELECT symbol_A AS symb, val1 AS valB
FROM `dbl014`
WHERE symbol_B = "Ga"
GROUP BY Symbol_A
UNION
SELECT symbol_B AS symb, val1 AS valB
FROM `dbl014`
WHERE (
symbol_A = "Ga"
AND symbol_B != ""
)
GROUP BY Symbol_B
) AS A
INNER JOIN (
SELECT symbol_A AS symb, val1 AS valC
FROM `dbl014`
WHERE symbol_B = "Y"
GROUP BY Symbol_A
UNION
SELECT symbol_B AS symb, val1 AS valC
FROM `dbl014`
WHERE (
symbol_A = "Y"
AND symbol_B != ""
)
GROUP BY Symbol_B
) AS B
USING ( symb )
) AS C
USING ( symb )
) AS D
USING ( symb )
ORDER BY symb
and voila!


a total of 42 all in all. The "val" columns are there for verificational purposes only – since after applying the GROUP BY function, they all lose their meanings.
A code to write code (as in a war to end -all- wars – 8P)
June 19, 2008 Posted by Emre S. Tasci
Lately, I’ve been studying on the nice and efficient algorithm of Dominik Endres and he’s been very helpful in replying to my relentless mails about the algorithm and the software. Now, if you have checked the algorithm, there is a part where iteration is needed to be done over the possible bin boundary distributions. Via a smart workaround he avoids this and uses a recursive equation.
For my needs, I want to follow the brute-force approach. To requote the situation, suppose we have K=4 number of classes, let’s label these as 0,1,2,3. There are 3 different ways to group these classes into 2 (M=2-1=1) bins obeying the following rules:
* There is always at least one classification per bin.
* Bins are adjascent to each other.
* Bins can not overlap.
The number of configurations are given by the formula:
N=(K-1)! / ( (K-M-1)! M!) (still haven’t brought back my latex renderer, sorry for that!)
and these 3 possible configurations for K=4, M=1 are:
|—-|—-|—-|
0 3 : Meaning, the first bin only covers the 0 class while the second bin covers 1, 2, 3.
1 3 : Meaning, the first bin covers 0, 1 while the second bin covers 2, 3.
2 3 : Meaning, the first bin covers 0, 1, 2 while the second bin covers 3.
Now, think that you are writing a code to get this values, it is easy when you pseudo-code it:
for k_0 = 0 : K-1-M
for k_1 = k_0+1 : K-M
…
for k_(K-3) = k_(K-4)+1 : K-4
for k_(K-2) = k_(K-3)+1 : K-3
print("k_0 – k_1 – … – k_(K-2) – K-1")
endfor
endfor
…
endfor
endfor
easier said than done because the number of the k_ variables and the for loops are changing with M.
So after some trying in Octave for recursive loops with the help of the feval() function, I gave up and wrote a PHP code that writes an Octave code and it was really fun! 8)
<?
//Support for command line variable passing:
for($i=1;$i<sizeof($_SERVER["argv"]);$i++)
{
list($var0,$val0) = explode("=",$_SERVER["argv"][$i]);
$_GET[$var0] = $val0;
}
$K = $_GET["K"];
$M = $_GET["M"];
if(!$_GET["K"])$_GET["K"] = 10;
if(!$_GET["M"])$_GET["M"] = 2;
if(!$_GET["f"])$_GET["f"] = "lol.m";
$fp = fopen($_GET["f"],"w");
fwrite($fp, "count=0;\n");
fwrite($fp, str_repeat("\t",$m)."for k0 = 0:".($K-$M-1)."\n");
for($m=1;$m<$M;$m++)
{
fwrite($fp, str_repeat("\t",$m)."for k".$m." = k".($m-1)."+1:".($K-$M-1+$m)."\n");
}
fwrite($fp, str_repeat("\t",$m)."printf(\"".str_repeat("%d – ",$M)."%d\\n\",");
for($i=0;$i<$m;$i++)
fwrite($fp, "k".$i.",");
fwrite($fp,($K-1).")\n");
fwrite($fp, str_repeat("\t",$m)."count++;\n");
for($m=$M-1;$m>=0;$m–)
{
fwrite($fp, str_repeat("\t",$m)."endfor\n");
}
fwrite($fp,"if(count!=factorial(".$K."-1)/(factorial(".$K."-".$M."-1)*factorial(".$M.")))\n\tprintf(\"Houston, we have a problem..\");\nendif\n");
//fwrite($fp,"printf(\"count : %d\\nfactorial : %d\\n\",count,factorial(".$K."-1)/(factorial(".$K."-".$M."-1)*factorial(".$M.")));\n");
fclose($fp);
system("octave ".$_GET["f"]);
?>
Now, if you call this code with for example:
> php genfor.php K=4 M=1
it produces and runs this Octave file lol.m:
count=0;
for k0 = 0:2
printf("%d – %d\n",k0,3)
count++;
endfor
if(count!=factorial(4-1)/(factorial(4-1-1)*factorial(1)))
printf("Houston, we have a problem..");
endif
which outputs:
0 – 3
1 – 3
2 – 3
And you get to keep your hands clean 8)
Later addition (27/6/2008) You can easily modify the code to also give you possible permutations for a set with K items and groups of M items (where ordering is not important). For example, for K=5, say {0,1,2,3,4} and M=4:
0-1-2-3
0-1-2-4
0-1-3-4
0-2-3-4
1-2-3-4
5 (=K!/(M!(K-M)!)) different sets.
The modifications we make to the code are:
* Add an optional parameter that will tell the code that, we want permutation instead of binning:
if($_GET["perm"]||$_GET["p"]||$_GET["P"])
{
$f_perm = TRUE;
$K+=1;
}
via the f_perm flag, we can check the type of the operation anywhere within the code. K is incremented because, previously, we were setting the end point fixed so that the last bin would always include the last point for the bins to cover all the space. But for permutationing we are not bounded by this fixication so, we have an additional freedom.
* Previously, we were just including the last point in the print() statement, we should fix this if we are permutating:
$str = "";
for($i=0;$i<$m;$i++)
$str .= "k".$i.",";
if(!$f_perm) fwrite($fp,$str.($K-1).")\n");
else fwrite($fp, substr($str,0,-1).")\n");
The reason for instead of now writing directly to the file in the iteration we just store it in a variable (str) is to deal with the trailing comma if we are permuting, as simple as that!
and the difference between before and after the modifications is:
sururi@dutsm0175 Octave $ diff genfor.php genfor2.php
10a11,16
> if($_GET["perm"]||$_GET["p"]||$_GET["P"])
> {
> $f_perm = TRUE;
> $K+=1;
> }
>
21c27,30
< fwrite($fp, str_repeat("\t",$m)."printf(\"".str_repeat("%d – ",$M)."%d\\n\",");
—
> if(!$f_perm)fwrite($fp, str_repeat("\t",$m)."printf(\"".str_repeat("%d – ",$M)."%d\\n\",");
> else fwrite($fp, str_repeat("\t",$m)."printf(\"".str_repeat("%d – ",($M-1))."%d\\n\",");
>
> $str = "";
24,25c33,35
< fwrite($fp, "k".$i.",");
< fwrite($fp,($K-1).")\n");
—
> $str .= "k".$i.",";
> if(!$f_perm) fwrite($fp,$str.($K-1).")\n");
> else fwrite($fp, substr($str,0,-1).")\n");
for the really lazy people (like myself), here is the whole deal! 8)
<?
//Support for command line variable passing:
for($i=1;$i<sizeof($_SERVER["argv"]);$i++)
{
list($var0,$val0) = explode("=",$_SERVER["argv"][$i]);
$_GET[$var0] = $val0;
}
$K = $_GET["K"];
$M = $_GET["M"];
if(!$_GET["K"])$_GET["K"] = 10;
if(!$_GET["M"])$_GET["M"] = 2;
if(!$_GET["f"])$_GET["f"] = "lol.m";
if($_GET["perm"]||$_GET["p"]||$_GET["P"])
{
$f_perm = TRUE;
$K+=1;
}
$fp = fopen($_GET["f"],"w");
fwrite($fp, "count=0;\n");
fwrite($fp, str_repeat("\t",$m)."for k0 = 0:".($K-$M-1)."\n");
for($m=1;$m<$M;$m++)
{
fwrite($fp, str_repeat("\t",$m)."for k".$m." = k".($m-1)."+1:".($K-$M-1+$m)."\n");
}
if(!$f_perm)fwrite($fp, str_repeat("\t",$m)."printf(\"".str_repeat("%d – ",$M)."%d\\n\",");
else fwrite($fp, str_repeat("\t",$m)."printf(\"".str_repeat("%d – ",($M-1))."%d\\n\",");
$str = "";
for($i=0;$i<$m;$i++)
$str .= "k".$i.",";
if(!$f_perm) fwrite($fp,$str.($K-1).")\n");
else fwrite($fp, substr($str,0,-1).")\n");
fwrite($fp, str_repeat("\t",$m)."count++;\n");
for($m=$M-1;$m>=0;$m–)
{
fwrite($fp, str_repeat("\t",$m)."endfor\n");
}
fwrite($fp,"if(count!=factorial(".$K."-1)/(factorial(".$K."-".$M."-1)*factorial(".$M.")))\n\tprintf(\"Houston, we have a problem..\");\nendif\n");
fwrite($fp,"printf(\"count : %d\\nfactorial : %d\\n\",count,factorial(".$K."-1)/(factorial(".$K."-".$M."-1)*factorial(".$M.")));\n");
fclose($fp);
system("octave ".$_GET["f"]);
?>
After the modifications,
php genfor.php K=5 M=3 p=1
will produce
0 – 1 – 2
0 – 1 – 3
0 – 1 – 4
0 – 2 – 3
0 – 2 – 4
0 – 3 – 4
1 – 2 – 3
1 – 2 – 4
1 – 3 – 4
2 – 3 – 4
Binning is easy (with eyes closed – misunderstanding all you see..)
June 2, 2008 Posted by Emre S. Tasci
When you have some nice discrete random variables, or more correctly, some sets of nice discrete random variables and given that they behave well (like the ones you encounter all the time in the textbook examples), calculating the entropies and then moving on to the deducing of mutual information between these sets is never difficult. But things don’t happen that well in real situations: they tend to get nastier. The methods you employ for binary-valued sets are useless when you have 17000 different type of data among 25000 data points.
As an example, consider these two sets:
A={1,2,3,4,5}
B={1,121,43,12,100}
which one would you say is more ordered? A? Really? But how? — each of them has 5 different values which would amount to the same entropy for both. Yes, you can define two new sets based on these sets with actually having the differences between two adjacent members:
A’ = {1,1,1,1}
B’ = {120,-78,-31,88}
and the answer is obvious. This is really assuring – except the fact that it doesn’t have to be this obvious and furthermore, you don’t usually get only 6 membered sets to try out variations.
For this problem of mine, I have been devising a method and I think it’s working well. It’s really simple, you just bin (down) your data according some criteria and if it goes well, at the end you have classified your data points in much more smaller number of bins.
Today, I re-found the works of Dominik Endres and his colleagues. Their binning method is called the Bayesian Binning (you can find the detailed information at Endres’ personal page) and it pretty looks solid. I’ll still be focusing on my method (which I humbly call Tracking the Eskimo and the method itself compared to the Bayesian Binning, seems very primitive) but it’s always nice to see that, someone also had a similar problem and worked his way through it. There is also the other thing which I mention from time to time : when you treat your information as data, you get to have nice tools that were developed not by researchers from your field of interest but from totally different disciplines who were also at one time visited the 101010 world. 8) (It turns out that Dominik Endres and his fellows are from Psychology. One other thing is that I had begun thinking about my method after seeing another method for cytometry (the scientific branch which counts the cells in blood flow – or smt like that 8) applications…)
References:
D. Endres and P. Földiák, Bayesian bin distribution inference and mutual information, IEEE Transactions on Information Theory, vol. 51, no. 11, pp. 3766-3779, November 2005 DOI: 10.1109/TIT.2005.856954
D. Endres and P. Földiák, Exact Bayesian Bin Classification: a fast alternative to Bayesian Classification and its application to neural response analysis,
Journal of Computational Neuroscience, 24(1): 24-35, 2008. DOI: 10.1007/s10827-007-0039-5.
D. Endres, M. Oram, J. Schindelin and P. Földiák, Bayesian binning beats approximate alternatives: estimating peri-stimulus time histograms,
pp. 393-400, Advances in Neural Information Processing Systems 20, MIT Press, Cambridge, MA, 2008 http://books.nips.cc/nips20.html


