Hex, Bugs and More Physics | Emre S. Tasci

from SVN to Mercurial

August 23, 2011 Posted by Emre S. Tasci

I’ve been using SVN for revision control system for some time. I certainly benefited from it to organize or fall-back to a stable version (“the good old times”) when I was in trouble while I was computing solo but there were two things that always upset me while using it:

Commiting meant publishing: This issue might be worked around when you have your trunk (we actually have the trunk for the ‘most recent’ status and a ‘released’ branch for the tested and stable programs of that trunk) and each of the developers play in their branches until it looks OK and hence merge it to trunk (and hopefully eventually make it to the ‘released’ branch), but the problem is, most of the time I’m in the middle of the coding process (in my branch) and it would be nice if I didn’t affect the main repository everytime I made a commit (it’s really not very nice) – in other words, even in my branch I would like to save while not making them available. The answer to this lies of course in distributed revision control systems (dvcs).
Merging: Merging is hell in SVN when you have many developers. Been there, suffered that.

I had heard of git and bazaar but -for some reasons I don’t know why- never had taken the step to give them a try. Very recently, in a scientific gathering, one of the participants suggested me to use mercurial. The interesting thing about this is, he was suggesting it as a means to enable an “undo” option for a -scientifing- refinement program which has the tendency to update your files in according to the changes you applied. I know this sounds natural but when you tried some method and it didn’t worked, you couldn’t go just one step back and use a different method – you have to start from scratch with your initial input file and apply the methods so far but the last consecutively over again. So, my friend was actually recommending me to use a revision control system for the work files (which can be done perfectly well via SVN, by the way) and he happened to be using mercurial. He suggested to check this website by Joel Spolsky (http://hginit.com/) to get it going and the website is very intriguing, indeed. So I have been running some tests to get my feet wet and it was going so well until I found that the log command didn’t reveal the list of the changes made upon the files per changeset (‘revision’ in terms of SVN). I searched and searched and at the end I found the solution on hg tip (http://hgtip.com/tips/advanced/2010-01-15-styling-mercurials-cli/) website by Steve Losh. His ‘Nice Log’ script was exactly what I was looking for plus some additional effective logging templates.

I don’t think for our big project I can make the switch from SVN to Mercurial, but from now on, I’ll be ‘hg init’ing instead of ‘svnadmin create’ing for the projects to come.

Filed in Coding | No Comments »

Exploring through the paths of subgroups, collecting indexes on the way…

June 6, 2011 Posted by Emre S. Tasci

Having a personal wiki has its pros and cons with the pros being obvious but, on the other hand, one doesn’t feel like reposting what he has already committed into the corresponding wikipedia entry (and since reposting means filtering out the sensitive information and generalizing it, it is double the effort). So this fact, more or less, explains my absence of activity in this blog for the last 1.5 years. But then, there is one negative aspect of personal wikipedia “blogging” – it’s like putting everything under the rug : you classify the data/information and then you forget that it is there. That’s when “actual” blogging (like this one) comes handy. So, sorry & welcome back..

Today, I’ll present a code that I’ve just written to parse out the compatible paths from a tree. In my case, the three is the list of subgroups with indexes that one can acquire using Bilbao Crystallographic Server’s marvelous SUBGROUPGRAPH tool. For low indexes, you can already have SUBGROUPGRAPH do this for you by specifying your supergroup G, subgroup H and the index [G:H]. For example, for G=136, H=14 and [G:H] = 8, you can have the following paths drawn:

subgroupgraph_tempfile963

But as I said, things can get rough when you have a high index. In that case, we can (and we will) try to parse and analyze the paths tree which is outputted by SUBGROUPGRAPH when no index is designated, e.g., for G=136, H=14:

maxsubs_subggraph

Where you see the maximal subgroups for the involved groups and their corresponding indexes. So, to go from P4_2/mnm (#136) to P2_1/c (#14) with index 8, we can follow the path:

P4_2/mnm (#136) –[2]–> Cmmm (#65) –[2]–> Pmna (#53) –[2]–> P2_1/c (#14)

with the related indexes given in the brackets totaling to 2x2x2 = 8.

The problem I had today was to find possible paths going from G=Fd-3m (#227) to H=Cc (#9) with index [G:H] = 192.

I first parsed the subgroup list into an array with their indexes, then followed the possible paths.

<?PHP
/* Emre S. Tasci <exxx.txxxx@ehu.es>                    *
 * By parsing the possible subgroup paths obtained from 
 * SUBGROUPGRAPH, finds the paths that are compatible 
 * with the given terminal super & sub groups and the 
 * designated index.
 *
 *                                              06/06/11 */

# Input Data === 0 ====================================================
$start_sup = 227;
$crit_index = 192;
$end_sub = 9;

$arr = file("data.txt"); # A sample of data.txt for the case of #227->#9
                         # is included at the end of the code.

# Input Data === 1 ====================================================

$arr_subs = Array();
$arr_labels = Array();
foreach($arr as $line)
{
    $auxarr = preg_split("/[ \t]+/",trim($line));
    #echo $auxarr[2]."\n";
    $sup = $auxarr[1];
    $suplabel = $auxarr[2];
    $arrsubs = split(";",$auxarr[3]);
    $arr_labels[$sup] = $suplabel;
    foreach($arrsubs as $subind)
    {
        $auxarr2 = Array();
        preg_match("/([0-9]+)\[([0-9]+)\]/",$subind,$auxarr2);
        #print_r($auxarr2);
        $sub = $auxarr2[1];
        $index = $auxarr2[2];
        $arr_subs[$sup][$index][] = $sub;
    }
}
#print_r($arr_subs);

# Start exploring
$start_sup = sprintf("%03d",$start_sup);
$end_sub = sprintf("%03d",$end_sub);
$arr_paths = Array();
$arr_paths[$start_sup] = 1;

findpath($start_sup);

function findpath($current_sup)
{
    global $arr_paths,$arr_subs,$crit_index,$end_sub;
    #echo "*".$current_sup."*\n";
    if(strrpos($current_sup,"-") !== FALSE)
    {
        $current_sup_last_sup = substr($current_sup,strrpos($current_sup,"-")+1);
        $current_sup_last_sup = substr($current_sup_last_sup,0,strpos($current_sup_last_sup,"["));
    }
        
    else
        $current_sup_last_sup = $current_sup;
    #echo "*".$current_sup_last_sup."*\n";
    $subindexes = array_keys($arr_subs[$current_sup_last_sup]);
    foreach($subindexes as $subindex)
    {
        $subs = $arr_subs[$current_sup_last_sup][$subindex];
        echo $subindex.": ".join(",",$subs)."\n";
        foreach($subs as $sub)
        {
            echo $current_sup."-".$sub."[".$subindex."]"."\n";
            $arr_paths[$current_sup."-".$sub."[".$subindex."]"] = $arr_paths[$current_sup] * $subindex;
            if($arr_paths[$current_sup."-".$sub."[".$subindex."]"]<$crit_index)
                findpath($current_sup."-".$sub."[".$subindex."]");
            elseif($arr_paths[$current_sup."-".$sub."[".$subindex."]"] == $crit_index && $sub == $end_sub)
                echo "\nPath Found: ".$current_sup."-".$sub."[".$subindex."]"."\n\n";
        }
    }
    #print_r($subindexes);
}
print_r($arr_paths);

/*
    data.txt:
1   227   Fd-3m   141[3];166[4];203[2];216[2]
2   220   I-43d   122[3];161[4]
3   219   F-43c   120[3];161[4];218[4]
4   218   P-43n   112[3];161[4];220[4]
5   217   I-43m   121[3];160[4];215[2];218[2]
6   216   F-43m   119[3];160[4];215[4]
7   215   P-43m   111[3];160[4];216[2];217[4];219[2]
8   203   Fd-3   070[3]
9   167   R-3c   015[3];161[2];165[3];167[4];167[5];167[7]
10   166   R-3m   012[3];160[2];164[3];166[2];166[4];166[5];166[7];167[2]
11   165   P-3c1   015[3];158[2];163[3];165[3];165[4];165[5];165[7]
12   164   P-3m1   012[3];156[2];162[3];164[2];164[3];164[4];164[5];164[7];165[2]
13   163   P-31c   015[3];159[2];163[3];163[4];163[5];163[7];165[3];167[3]
14   162   P-31m   012[3];157[2];162[2];162[3];162[4];162[5];162[7];163[2];164[3];166[3]
15   161   R3c   009[3];158[3];161[4];161[5];161[7]
16   160   R3m   008[3];156[3];160[2];160[4];160[5];160[7];161[2]
17   159   P31c   009[3];158[3];159[3];159[4];159[5];159[7];161[3]
18   158   P3c1   009[3];158[3];158[4];158[5];158[7];159[3]
19   157   P31m   008[3];156[3];157[2];157[3];157[4];157[5];157[7];159[2];160[3]
20   156   P3m1   008[3];156[2];156[3];156[4];156[5];156[7];157[3];158[2]
21   141   I41/amd   070[2];074[2];088[2];109[2];119[2];122[2];141[3];141[5];141[7];141[9]
22   122   I-42d   043[2];122[3];122[5];122[7];122[9]
23   121   I-42m   042[2];111[2];112[2];113[2];114[2];121[3];121[5];121[7];121[9]
24   120   I-4c2   045[2];116[2];117[2];120[3];120[5];120[7];120[9]
25   119   I-4m2   044[2];115[2];118[2];119[3];119[5];119[7];119[9]
26   118   P-4n2   034[2];118[3];118[5];118[7];118[9];122[2]
27   117   P-4b2   032[2];117[2];117[3];117[5];117[7];117[9];118[2]
28   116   P-4c2   027[2];112[2];114[2];116[3];116[5];116[7];116[9]
29   115   P-4m2   025[2];111[2];113[2];115[2];115[3];115[5];115[7];115[9];116[2];121[2]
30   114   P-421c   037[2];114[3];114[5];114[7];114[9]
31   113   P-421m   035[2];113[2];113[3];113[5];113[7];113[9];114[2]
32   112   P-42c   037[2];112[3];112[5];112[7];112[9];116[2];118[2]
33   111   P-42m   035[2];111[2];111[3];111[5];111[7];111[9];112[2];115[2];117[2];119[2];120[2]
34   109   I41md   043[2];044[2];109[3];109[5];109[7];109[9]
35   088   I41/a   015[2];088[3];088[5];088[7];088[9]
36   074   Imma   012[2];015[2];044[2];046[2];051[2];052[2];053[2];062[2];074[3];074[5];074[7]
37   070   Fddd   015[2];043[2];070[3];070[5];070[7]
38   064   Cmce   012[2];014[2];015[2];036[2];039[2];041[2];053[2];054[2];055[2];056[2];057[2];060[2];061[2];062[2];064[3];064[5];064[7]
39   063   Cmcm   011[2];012[2];015[2];036[2];038[2];040[2];051[2];052[2];057[2];058[2];059[2];060[2];062[2];063[3];063[5];063[7]
40   062   Pnma   011[2];014[2];026[2];031[2];033[2];062[3];062[5];062[7]
41   061   Pbca   014[2];029[2];061[3];061[5];061[7]
42   060   Pbcn   013[2];014[2];029[2];030[2];033[2];060[3];060[5];060[7]
43   059   Pmmn   011[2];013[2];025[2];031[2];056[2];059[2];059[3];059[5];059[7];062[2]
44   058   Pnnm   010[2];014[2];031[2];034[2];058[3];058[5];058[7]
45   057   Pbcm   011[2];013[2];014[2];026[2];028[2];029[2];057[2];057[3];057[5];057[7];060[2];061[2];062[2]
46   056   Pccn   013[2];014[2];027[2];033[2];056[3];056[5];056[7]
47   055   Pbam   010[2];014[2];026[2];032[2];055[2];055[3];055[5];055[7];058[2];062[2]
48   054   Pcca   013[2];014[2];027[2];029[2];032[2];052[2];054[2];054[3];054[5];054[7];056[2];060[2]
49   053   Pmna   010[2];013[2];014[2];028[2];030[2];031[2];052[2];053[2];053[3];053[5];053[7];058[2];060[2]
50   052   Pnna   013[2];014[2];030[2];033[2];034[2];052[3];052[5];052[7]
51   051   Pmma   010[2];011[2];013[2];025[2];026[2];028[2];051[2];051[3];051[5];051[7];053[2];054[2];055[2];057[2];059[2];063[2];064[2]
52   046   Ima2   008[2];009[2];026[2];028[2];030[2];033[2];046[3];046[5];046[7]
53   045   Iba2   009[2];027[2];029[2];032[2];045[3];045[5];045[7]
54   044   Imm2   008[2];025[2];031[2];034[2];044[3];044[5];044[7]
55   043   Fdd2   009[2];043[3];043[5];043[7]
56   042   Fmm2   008[2];035[2];036[2];037[2];038[2];039[2];040[2];041[2];042[3];042[5];042[7]
57   041   Aea2   007[2];009[2];029[2];030[2];032[2];033[2];041[3];041[5];041[7]
58   040   Ama2   006[2];009[2];028[2];031[2];033[2];034[2];040[3];040[5];040[7]
59   039   Aem2   007[2];008[2];026[2];027[2];028[2];029[2];039[2];039[3];039[5];039[7];041[2];045[2];046[2]
60   038   Amm2   006[2];008[2];025[2];026[2];030[2];031[2];038[2];038[3];038[5];038[7];040[2];044[2];046[2]
61   037   Ccc2   009[2];027[2];030[2];034[2];037[3];037[5];037[7]
62   036   Cmc21   008[2];009[2];026[2];029[2];031[2];033[2];036[3];036[5];036[7]
63   035   Cmm2   008[2];025[2];028[2];032[2];035[2];035[3];035[5];035[7];036[2];037[2];044[2];045[2];046[2]
64   034   Pnn2   007[2];034[3];034[5];034[7];043[2]
65   033   Pna21   007[2];033[3];033[5];033[7]
66   032   Pba2   007[2];032[2];032[3];032[5];032[7];033[2];034[2]
67   031   Pmn21   006[2];007[2];031[2];031[3];031[5];031[7];033[2]
68   030   Pnc2   007[2];030[2];030[3];030[5];030[7];034[2]
69   029   Pca21   007[2];029[2];029[3];029[5];029[7];033[2]
70   028   Pma2   006[2];007[2];028[2];028[3];028[5];028[7];029[2];030[2];031[2];032[2];040[2];041[2]
71   027   Pcc2   007[2];027[2];027[3];027[5];027[7];030[2];037[2]
72   026   Pmc21   006[2];007[2];026[2];026[3];026[5];026[7];029[2];031[2];036[2]
73   025   Pmm2   006[2];025[2];025[3];025[5];025[7];026[2];027[2];028[2];035[2];038[2];039[2];042[2]
74   015   C2/c   009[2];013[2];014[2];015[3];015[5];015[7]
75   014   P21/c   007[2];014[2];014[3];014[5];014[7]
76   013   P2/c   007[2];013[2];013[3];013[5];013[7];014[2];015[2]
77   012   C2/m   008[2];010[2];011[2];012[2];012[3];012[5];012[7];013[2];014[2];015[2]
78   011   P21/m   006[2];011[2];011[3];011[5];011[7];014[2]
79   010   P2/m   006[2];010[2];010[3];010[5];010[7];011[2];012[2];013[2]
80   008   Cm   006[2];007[2];008[2];008[3];008[5];008[7];009[2]
81   007   Pc   007[2];007[3];007[5];007[7];009[2]
82   006   Pm   006[2];006[3];006[5];006[7];007[2];008[2]
83   009   Cc   007[2];009[3];009[5];009[7]
 */

When run, the code lists all the paths with the matching ones preceded by “Path Found”, so if you grep wrt it, you’ll have, for this example:

sururi@husniya:/xxx$ php find_trpath_for_index.php |grep Path|sed "s:Path Found\: ::"
227-141[3]-070[2]-015[2]-009[2]-007[2]-007[2]-009[2]
227-141[3]-070[2]-015[2]-013[2]-007[2]-007[2]-009[2]
227-141[3]-070[2]-015[2]-013[2]-013[2]-007[2]-009[2]
227-141[3]-070[2]-015[2]-013[2]-013[2]-015[2]-009[2]
227-141[3]-070[2]-015[2]-013[2]-014[2]-007[2]-009[2]
227-141[3]-070[2]-015[2]-014[2]-007[2]-007[2]-009[2]
227-141[3]-070[2]-015[2]-014[2]-014[2]-007[2]-009[2]
227-141[3]-070[2]-043[2]-009[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-008[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-008[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-012[2]-008[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-008[2]-008[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-008[2]-008[2]-008[2]-009[2]
227-141[3]-074[2]-012[2]-008[2]-009[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-010[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-010[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-012[2]-010[2]-012[2]-008[2]-009[2]
227-141[3]-074[2]-012[2]-010[2]-012[2]-015[2]-009[2]
227-141[3]-074[2]-012[2]-010[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-010[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-012[2]-011[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-011[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-012[2]-011[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-012[2]-008[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-012[2]-008[2]-008[2]-009[2]
227-141[3]-074[2]-012[2]-012[2]-012[2]-008[2]-009[2]
227-141[3]-074[2]-012[2]-012[2]-012[2]-015[2]-009[2]
227-141[3]-074[2]-012[2]-012[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-012[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-012[2]-012[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-013[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-013[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-013[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-012[2]-013[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-014[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-014[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-015[2]-009[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-015[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-012[2]-015[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-012[2]-015[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-015[2]-009[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-015[2]-013[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-015[2]-013[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-015[2]-013[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-015[2]-013[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-015[2]-014[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-015[2]-014[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-044[2]-008[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-044[2]-008[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-044[2]-008[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-044[2]-008[2]-008[2]-007[2]-009[2]
227-141[3]-074[2]-044[2]-008[2]-008[2]-008[2]-009[2]
227-141[3]-074[2]-044[2]-008[2]-009[2]-007[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-026[2]-007[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-026[2]-036[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-027[2]-007[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-027[2]-037[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-028[2]-007[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-028[2]-040[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-028[2]-041[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-035[2]-008[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-035[2]-036[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-035[2]-037[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-035[2]-045[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-035[2]-046[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-038[2]-008[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-038[2]-040[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-038[2]-046[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-039[2]-007[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-039[2]-008[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-039[2]-041[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-039[2]-045[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-039[2]-046[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-042[2]-008[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-042[2]-036[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-042[2]-037[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-042[2]-040[2]-009[2]
227-141[3]-074[2]-044[2]-025[2]-042[2]-041[2]-009[2]
227-141[3]-074[2]-044[2]-031[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-044[2]-031[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-044[2]-031[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-044[2]-031[2]-031[2]-007[2]-009[2]
227-141[3]-074[2]-044[2]-031[2]-033[2]-007[2]-009[2]
227-141[3]-074[2]-044[2]-034[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-008[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-008[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-046[2]-008[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-008[2]-008[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-008[2]-008[2]-008[2]-009[2]
227-141[3]-074[2]-046[2]-008[2]-009[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-009[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-026[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-026[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-046[2]-026[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-026[2]-026[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-026[2]-026[2]-036[2]-009[2]
227-141[3]-074[2]-046[2]-026[2]-029[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-026[2]-031[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-026[2]-036[2]-008[2]-009[2]
227-141[3]-074[2]-046[2]-028[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-028[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-046[2]-028[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-028[2]-028[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-028[2]-028[2]-040[2]-009[2]
227-141[3]-074[2]-046[2]-028[2]-028[2]-041[2]-009[2]
227-141[3]-074[2]-046[2]-028[2]-029[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-028[2]-030[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-028[2]-031[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-028[2]-032[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-028[2]-041[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-030[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-030[2]-030[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-030[2]-034[2]-007[2]-009[2]
227-141[3]-074[2]-046[2]-030[2]-034[2]-043[2]-009[2]
227-141[3]-074[2]-046[2]-033[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-010[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-010[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-010[2]-012[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-010[2]-012[2]-015[2]-009[2]
227-141[3]-074[2]-051[2]-010[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-010[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-051[2]-011[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-011[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-011[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-013[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-013[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-013[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-051[2]-013[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-026[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-026[2]-036[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-027[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-027[2]-037[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-028[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-028[2]-040[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-028[2]-041[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-035[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-035[2]-036[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-035[2]-037[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-035[2]-045[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-035[2]-046[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-038[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-038[2]-040[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-038[2]-046[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-039[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-039[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-039[2]-041[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-039[2]-045[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-039[2]-046[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-042[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-042[2]-036[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-042[2]-037[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-042[2]-040[2]-009[2]
227-141[3]-074[2]-051[2]-025[2]-042[2]-041[2]-009[2]
227-141[3]-074[2]-051[2]-026[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-026[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-026[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-026[2]-026[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-026[2]-026[2]-036[2]-009[2]
227-141[3]-074[2]-051[2]-026[2]-029[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-026[2]-031[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-026[2]-036[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-028[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-028[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-028[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-028[2]-028[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-028[2]-028[2]-040[2]-009[2]
227-141[3]-074[2]-051[2]-028[2]-028[2]-041[2]-009[2]
227-141[3]-074[2]-051[2]-028[2]-029[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-028[2]-030[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-028[2]-031[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-028[2]-032[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-028[2]-041[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-051[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-051[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-051[2]-051[2]-026[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-051[2]-026[2]-036[2]-009[2]
227-141[3]-074[2]-051[2]-051[2]-028[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-051[2]-028[2]-040[2]-009[2]
227-141[3]-074[2]-051[2]-051[2]-028[2]-041[2]-009[2]
227-141[3]-074[2]-051[2]-051[2]-063[2]-015[2]-009[2]
227-141[3]-074[2]-051[2]-051[2]-063[2]-036[2]-009[2]
227-141[3]-074[2]-051[2]-051[2]-063[2]-040[2]-009[2]
227-141[3]-074[2]-051[2]-051[2]-064[2]-015[2]-009[2]
227-141[3]-074[2]-051[2]-051[2]-064[2]-036[2]-009[2]
227-141[3]-074[2]-051[2]-051[2]-064[2]-041[2]-009[2]
227-141[3]-074[2]-051[2]-053[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-053[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-051[2]-053[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-053[2]-028[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-053[2]-028[2]-040[2]-009[2]
227-141[3]-074[2]-051[2]-053[2]-028[2]-041[2]-009[2]
227-141[3]-074[2]-051[2]-053[2]-030[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-053[2]-031[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-054[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-054[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-051[2]-054[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-054[2]-027[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-054[2]-027[2]-037[2]-009[2]
227-141[3]-074[2]-051[2]-054[2]-029[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-054[2]-032[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-055[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-055[2]-026[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-055[2]-026[2]-036[2]-009[2]
227-141[3]-074[2]-051[2]-055[2]-032[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-057[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-057[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-051[2]-057[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-057[2]-026[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-057[2]-026[2]-036[2]-009[2]
227-141[3]-074[2]-051[2]-057[2]-028[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-057[2]-028[2]-040[2]-009[2]
227-141[3]-074[2]-051[2]-057[2]-028[2]-041[2]-009[2]
227-141[3]-074[2]-051[2]-057[2]-029[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-059[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-059[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-051[2]-059[2]-031[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-063[2]-012[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-063[2]-012[2]-015[2]-009[2]
227-141[3]-074[2]-051[2]-063[2]-036[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-063[2]-038[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-063[2]-038[2]-040[2]-009[2]
227-141[3]-074[2]-051[2]-063[2]-038[2]-046[2]-009[2]
227-141[3]-074[2]-051[2]-064[2]-012[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-064[2]-012[2]-015[2]-009[2]
227-141[3]-074[2]-051[2]-064[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-064[2]-036[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-064[2]-039[2]-007[2]-009[2]
227-141[3]-074[2]-051[2]-064[2]-039[2]-008[2]-009[2]
227-141[3]-074[2]-051[2]-064[2]-039[2]-041[2]-009[2]
227-141[3]-074[2]-051[2]-064[2]-039[2]-045[2]-009[2]
227-141[3]-074[2]-051[2]-064[2]-039[2]-046[2]-009[2]
227-141[3]-074[2]-051[2]-064[2]-041[2]-007[2]-009[2]
227-141[3]-074[2]-052[2]-013[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-052[2]-013[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-052[2]-013[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-052[2]-013[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-052[2]-014[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-052[2]-014[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-052[2]-030[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-052[2]-030[2]-030[2]-007[2]-009[2]
227-141[3]-074[2]-052[2]-030[2]-034[2]-007[2]-009[2]
227-141[3]-074[2]-052[2]-030[2]-034[2]-043[2]-009[2]
227-141[3]-074[2]-052[2]-033[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-052[2]-034[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-010[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-010[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-053[2]-010[2]-012[2]-008[2]-009[2]
227-141[3]-074[2]-053[2]-010[2]-012[2]-015[2]-009[2]
227-141[3]-074[2]-053[2]-010[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-010[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-053[2]-013[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-013[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-013[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-053[2]-013[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-014[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-014[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-028[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-028[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-053[2]-028[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-028[2]-028[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-028[2]-028[2]-040[2]-009[2]
227-141[3]-074[2]-053[2]-028[2]-028[2]-041[2]-009[2]
227-141[3]-074[2]-053[2]-028[2]-029[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-028[2]-030[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-028[2]-031[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-028[2]-032[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-028[2]-041[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-030[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-030[2]-030[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-030[2]-034[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-030[2]-034[2]-043[2]-009[2]
227-141[3]-074[2]-053[2]-031[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-031[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-053[2]-031[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-031[2]-031[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-031[2]-033[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-052[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-052[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-053[2]-052[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-052[2]-030[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-052[2]-033[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-052[2]-034[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-052[2]-034[2]-043[2]-009[2]
227-141[3]-074[2]-053[2]-053[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-053[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-053[2]-053[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-053[2]-028[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-053[2]-028[2]-040[2]-009[2]
227-141[3]-074[2]-053[2]-053[2]-028[2]-041[2]-009[2]
227-141[3]-074[2]-053[2]-053[2]-030[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-053[2]-031[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-058[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-058[2]-031[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-058[2]-034[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-058[2]-034[2]-043[2]-009[2]
227-141[3]-074[2]-053[2]-060[2]-013[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-060[2]-013[2]-015[2]-009[2]
227-141[3]-074[2]-053[2]-060[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-060[2]-029[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-060[2]-030[2]-007[2]-009[2]
227-141[3]-074[2]-053[2]-060[2]-033[2]-007[2]-009[2]
227-141[3]-074[2]-062[2]-011[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-062[2]-011[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-062[2]-011[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-062[2]-014[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-062[2]-014[2]-014[2]-007[2]-009[2]
227-141[3]-074[2]-062[2]-026[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-062[2]-026[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-062[2]-026[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-062[2]-026[2]-026[2]-007[2]-009[2]
227-141[3]-074[2]-062[2]-026[2]-026[2]-036[2]-009[2]
227-141[3]-074[2]-062[2]-026[2]-029[2]-007[2]-009[2]
227-141[3]-074[2]-062[2]-026[2]-031[2]-007[2]-009[2]
227-141[3]-074[2]-062[2]-026[2]-036[2]-008[2]-009[2]
227-141[3]-074[2]-062[2]-031[2]-006[2]-007[2]-009[2]
227-141[3]-074[2]-062[2]-031[2]-006[2]-008[2]-009[2]
227-141[3]-074[2]-062[2]-031[2]-007[2]-007[2]-009[2]
227-141[3]-074[2]-062[2]-031[2]-031[2]-007[2]-009[2]
227-141[3]-074[2]-062[2]-031[2]-033[2]-007[2]-009[2]
227-141[3]-074[2]-062[2]-033[2]-007[2]-007[2]-009[2]
227-141[3]-088[2]-015[2]-009[2]-007[2]-007[2]-009[2]
227-141[3]-088[2]-015[2]-013[2]-007[2]-007[2]-009[2]
227-141[3]-088[2]-015[2]-013[2]-013[2]-007[2]-009[2]
227-141[3]-088[2]-015[2]-013[2]-013[2]-015[2]-009[2]
227-141[3]-088[2]-015[2]-013[2]-014[2]-007[2]-009[2]
227-141[3]-088[2]-015[2]-014[2]-007[2]-007[2]-009[2]
227-141[3]-088[2]-015[2]-014[2]-014[2]-007[2]-009[2]
227-141[3]-109[2]-043[2]-009[2]-007[2]-007[2]-009[2]
227-141[3]-109[2]-044[2]-008[2]-006[2]-007[2]-009[2]
227-141[3]-109[2]-044[2]-008[2]-006[2]-008[2]-009[2]
227-141[3]-109[2]-044[2]-008[2]-007[2]-007[2]-009[2]
227-141[3]-109[2]-044[2]-008[2]-008[2]-007[2]-009[2]
227-141[3]-109[2]-044[2]-008[2]-008[2]-008[2]-009[2]
227-141[3]-109[2]-044[2]-008[2]-009[2]-007[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-006[2]-007[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-006[2]-008[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-026[2]-007[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-026[2]-036[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-027[2]-007[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-027[2]-037[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-028[2]-007[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-028[2]-040[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-028[2]-041[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-035[2]-008[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-035[2]-036[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-035[2]-037[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-035[2]-045[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-035[2]-046[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-038[2]-008[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-038[2]-040[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-038[2]-046[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-039[2]-007[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-039[2]-008[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-039[2]-041[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-039[2]-045[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-039[2]-046[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-042[2]-008[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-042[2]-036[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-042[2]-037[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-042[2]-040[2]-009[2]
227-141[3]-109[2]-044[2]-025[2]-042[2]-041[2]-009[2]
227-141[3]-109[2]-044[2]-031[2]-006[2]-007[2]-009[2]
227-141[3]-109[2]-044[2]-031[2]-006[2]-008[2]-009[2]
227-141[3]-109[2]-044[2]-031[2]-007[2]-007[2]-009[2]
227-141[3]-109[2]-044[2]-031[2]-031[2]-007[2]-009[2]
227-141[3]-109[2]-044[2]-031[2]-033[2]-007[2]-009[2]
227-141[3]-109[2]-044[2]-034[2]-007[2]-007[2]-009[2]
227-141[3]-119[2]-044[2]-008[2]-006[2]-007[2]-009[2]
227-141[3]-119[2]-044[2]-008[2]-006[2]-008[2]-009[2]
227-141[3]-119[2]-044[2]-008[2]-007[2]-007[2]-009[2]
227-141[3]-119[2]-044[2]-008[2]-008[2]-007[2]-009[2]
227-141[3]-119[2]-044[2]-008[2]-008[2]-008[2]-009[2]
227-141[3]-119[2]-044[2]-008[2]-009[2]-007[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-006[2]-007[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-006[2]-008[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-026[2]-007[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-026[2]-036[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-027[2]-007[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-027[2]-037[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-028[2]-007[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-028[2]-040[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-028[2]-041[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-035[2]-008[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-035[2]-036[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-035[2]-037[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-035[2]-045[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-035[2]-046[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-038[2]-008[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-038[2]-040[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-038[2]-046[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-039[2]-007[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-039[2]-008[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-039[2]-041[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-039[2]-045[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-039[2]-046[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-042[2]-008[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-042[2]-036[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-042[2]-037[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-042[2]-040[2]-009[2]
227-141[3]-119[2]-044[2]-025[2]-042[2]-041[2]-009[2]
227-141[3]-119[2]-044[2]-031[2]-006[2]-007[2]-009[2]
227-141[3]-119[2]-044[2]-031[2]-006[2]-008[2]-009[2]
227-141[3]-119[2]-044[2]-031[2]-007[2]-007[2]-009[2]
227-141[3]-119[2]-044[2]-031[2]-031[2]-007[2]-009[2]
227-141[3]-119[2]-044[2]-031[2]-033[2]-007[2]-009[2]
227-141[3]-119[2]-044[2]-034[2]-007[2]-007[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-006[2]-007[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-006[2]-008[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-026[2]-007[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-026[2]-036[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-027[2]-007[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-027[2]-037[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-028[2]-007[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-028[2]-040[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-028[2]-041[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-035[2]-008[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-035[2]-036[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-035[2]-037[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-035[2]-045[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-035[2]-046[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-038[2]-008[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-038[2]-040[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-038[2]-046[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-039[2]-007[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-039[2]-008[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-039[2]-041[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-039[2]-045[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-039[2]-046[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-042[2]-008[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-042[2]-036[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-042[2]-037[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-042[2]-040[2]-009[2]
227-141[3]-119[2]-115[2]-025[2]-042[2]-041[2]-009[2]
227-141[3]-119[2]-115[2]-111[2]-035[2]-008[2]-009[2]
227-141[3]-119[2]-115[2]-111[2]-035[2]-036[2]-009[2]
227-141[3]-119[2]-115[2]-111[2]-035[2]-037[2]-009[2]
227-141[3]-119[2]-115[2]-111[2]-035[2]-045[2]-009[2]
227-141[3]-119[2]-115[2]-111[2]-035[2]-046[2]-009[2]
227-141[3]-119[2]-115[2]-111[2]-112[2]-037[2]-009[2]
227-141[3]-119[2]-115[2]-111[2]-120[2]-045[2]-009[2]
227-141[3]-119[2]-115[2]-113[2]-035[2]-008[2]-009[2]
227-141[3]-119[2]-115[2]-113[2]-035[2]-036[2]-009[2]
227-141[3]-119[2]-115[2]-113[2]-035[2]-037[2]-009[2]
227-141[3]-119[2]-115[2]-113[2]-035[2]-045[2]-009[2]
227-141[3]-119[2]-115[2]-113[2]-035[2]-046[2]-009[2]
227-141[3]-119[2]-115[2]-113[2]-114[2]-037[2]-009[2]
227-141[3]-119[2]-115[2]-116[2]-027[2]-007[2]-009[2]
227-141[3]-119[2]-115[2]-116[2]-027[2]-037[2]-009[2]
227-141[3]-119[2]-115[2]-116[2]-112[2]-037[2]-009[2]
227-141[3]-119[2]-115[2]-116[2]-114[2]-037[2]-009[2]
227-141[3]-119[2]-115[2]-121[2]-042[2]-008[2]-009[2]
227-141[3]-119[2]-115[2]-121[2]-042[2]-036[2]-009[2]
227-141[3]-119[2]-115[2]-121[2]-042[2]-037[2]-009[2]
227-141[3]-119[2]-115[2]-121[2]-042[2]-040[2]-009[2]
227-141[3]-119[2]-115[2]-121[2]-042[2]-041[2]-009[2]
227-141[3]-119[2]-115[2]-121[2]-112[2]-037[2]-009[2]
227-141[3]-119[2]-115[2]-121[2]-114[2]-037[2]-009[2]
227-141[3]-119[2]-118[2]-034[2]-007[2]-007[2]-009[2]
227-141[3]-122[2]-043[2]-009[2]-007[2]-007[2]-009[2]
227-166[4]-012[3]-008[2]-006[2]-007[2]-009[2]
227-166[4]-012[3]-008[2]-006[2]-008[2]-009[2]
227-166[4]-012[3]-008[2]-007[2]-007[2]-009[2]
227-166[4]-012[3]-008[2]-008[2]-007[2]-009[2]
227-166[4]-012[3]-008[2]-008[2]-008[2]-009[2]
227-166[4]-012[3]-008[2]-009[2]-007[2]-009[2]
227-166[4]-012[3]-010[2]-006[2]-007[2]-009[2]
227-166[4]-012[3]-010[2]-006[2]-008[2]-009[2]
227-166[4]-012[3]-010[2]-012[2]-008[2]-009[2]
227-166[4]-012[3]-010[2]-012[2]-015[2]-009[2]
227-166[4]-012[3]-010[2]-013[2]-007[2]-009[2]
227-166[4]-012[3]-010[2]-013[2]-015[2]-009[2]
227-166[4]-012[3]-011[2]-006[2]-007[2]-009[2]
227-166[4]-012[3]-011[2]-006[2]-008[2]-009[2]
227-166[4]-012[3]-011[2]-014[2]-007[2]-009[2]
227-166[4]-012[3]-012[2]-008[2]-007[2]-009[2]
227-166[4]-012[3]-012[2]-008[2]-008[2]-009[2]
227-166[4]-012[3]-012[2]-012[2]-008[2]-009[2]
227-166[4]-012[3]-012[2]-012[2]-015[2]-009[2]
227-166[4]-012[3]-012[2]-013[2]-007[2]-009[2]
227-166[4]-012[3]-012[2]-013[2]-015[2]-009[2]
227-166[4]-012[3]-012[2]-014[2]-007[2]-009[2]
227-166[4]-012[3]-013[2]-007[2]-007[2]-009[2]
227-166[4]-012[3]-013[2]-013[2]-007[2]-009[2]
227-166[4]-012[3]-013[2]-013[2]-015[2]-009[2]
227-166[4]-012[3]-013[2]-014[2]-007[2]-009[2]
227-166[4]-012[3]-014[2]-007[2]-007[2]-009[2]
227-166[4]-012[3]-014[2]-014[2]-007[2]-009[2]
227-166[4]-012[3]-015[2]-009[2]-007[2]-009[2]
227-166[4]-012[3]-015[2]-013[2]-007[2]-009[2]
227-166[4]-012[3]-015[2]-013[2]-015[2]-009[2]
227-166[4]-012[3]-015[2]-014[2]-007[2]-009[2]
227-166[4]-160[2]-008[3]-006[2]-007[2]-009[2]
227-166[4]-160[2]-008[3]-006[2]-008[2]-009[2]
227-166[4]-160[2]-008[3]-007[2]-007[2]-009[2]
227-166[4]-160[2]-008[3]-008[2]-007[2]-009[2]
227-166[4]-160[2]-008[3]-008[2]-008[2]-009[2]
227-166[4]-160[2]-008[3]-009[2]-007[2]-009[2]
227-166[4]-160[2]-160[2]-008[3]-007[2]-009[2]
227-166[4]-160[2]-160[2]-008[3]-008[2]-009[2]
227-166[4]-160[2]-160[2]-160[2]-008[3]-009[2]
227-166[4]-160[2]-160[2]-160[2]-161[2]-009[3]
227-166[4]-160[2]-161[2]-009[3]-007[2]-009[2]
227-166[4]-160[2]-161[2]-161[4]-009[3]
227-166[4]-160[2]-160[4]-008[3]-009[2]
227-166[4]-160[2]-160[4]-161[2]-009[3]
227-166[4]-166[2]-012[3]-008[2]-007[2]-009[2]
227-166[4]-166[2]-012[3]-008[2]-008[2]-009[2]
227-166[4]-166[2]-012[3]-012[2]-008[2]-009[2]
227-166[4]-166[2]-012[3]-012[2]-015[2]-009[2]
227-166[4]-166[2]-012[3]-013[2]-007[2]-009[2]
227-166[4]-166[2]-012[3]-013[2]-015[2]-009[2]
227-166[4]-166[2]-012[3]-014[2]-007[2]-009[2]
227-166[4]-166[2]-160[2]-008[3]-007[2]-009[2]
227-166[4]-166[2]-160[2]-008[3]-008[2]-009[2]
227-166[4]-166[2]-160[2]-160[2]-008[3]-009[2]
227-166[4]-166[2]-160[2]-160[2]-161[2]-009[3]
227-166[4]-166[2]-166[2]-012[3]-008[2]-009[2]
227-166[4]-166[2]-166[2]-012[3]-015[2]-009[2]
227-166[4]-166[2]-166[2]-160[2]-008[3]-009[2]
227-166[4]-166[2]-166[2]-160[2]-161[2]-009[3]
227-166[4]-166[2]-166[2]-167[2]-015[3]-009[2]
227-166[4]-166[2]-166[2]-167[2]-161[2]-009[3]
227-166[4]-167[2]-015[3]-009[2]-007[2]-009[2]
227-166[4]-167[2]-015[3]-013[2]-007[2]-009[2]
227-166[4]-167[2]-015[3]-013[2]-015[2]-009[2]
227-166[4]-167[2]-015[3]-014[2]-007[2]-009[2]
227-166[4]-167[2]-161[2]-009[3]-007[2]-009[2]
227-166[4]-167[2]-161[2]-161[4]-009[3]
227-166[4]-167[2]-167[4]-015[3]-009[2]
227-166[4]-167[2]-167[4]-161[2]-009[3]
227-166[4]-166[4]-012[3]-008[2]-009[2]
227-166[4]-166[4]-012[3]-015[2]-009[2]
227-166[4]-166[4]-160[2]-008[3]-009[2]
227-166[4]-166[4]-160[2]-161[2]-009[3]
227-166[4]-166[4]-167[2]-015[3]-009[2]
227-166[4]-166[4]-167[2]-161[2]-009[3]
227-203[2]-070[3]-015[2]-009[2]-007[2]-007[2]-009[2]
227-203[2]-070[3]-015[2]-013[2]-007[2]-007[2]-009[2]
227-203[2]-070[3]-015[2]-013[2]-013[2]-007[2]-009[2]
227-203[2]-070[3]-015[2]-013[2]-013[2]-015[2]-009[2]
227-203[2]-070[3]-015[2]-013[2]-014[2]-007[2]-009[2]
227-203[2]-070[3]-015[2]-014[2]-007[2]-007[2]-009[2]
227-203[2]-070[3]-015[2]-014[2]-014[2]-007[2]-009[2]
227-203[2]-070[3]-043[2]-009[2]-007[2]-007[2]-009[2]
227-216[2]-119[3]-044[2]-008[2]-006[2]-007[2]-009[2]
227-216[2]-119[3]-044[2]-008[2]-006[2]-008[2]-009[2]
227-216[2]-119[3]-044[2]-008[2]-007[2]-007[2]-009[2]
227-216[2]-119[3]-044[2]-008[2]-008[2]-007[2]-009[2]
227-216[2]-119[3]-044[2]-008[2]-008[2]-008[2]-009[2]
227-216[2]-119[3]-044[2]-008[2]-009[2]-007[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-006[2]-007[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-006[2]-008[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-026[2]-007[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-026[2]-036[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-027[2]-007[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-027[2]-037[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-028[2]-007[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-028[2]-040[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-028[2]-041[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-035[2]-008[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-035[2]-036[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-035[2]-037[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-035[2]-045[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-035[2]-046[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-038[2]-008[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-038[2]-040[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-038[2]-046[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-039[2]-007[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-039[2]-008[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-039[2]-041[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-039[2]-045[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-039[2]-046[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-042[2]-008[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-042[2]-036[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-042[2]-037[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-042[2]-040[2]-009[2]
227-216[2]-119[3]-044[2]-025[2]-042[2]-041[2]-009[2]
227-216[2]-119[3]-044[2]-031[2]-006[2]-007[2]-009[2]
227-216[2]-119[3]-044[2]-031[2]-006[2]-008[2]-009[2]
227-216[2]-119[3]-044[2]-031[2]-007[2]-007[2]-009[2]
227-216[2]-119[3]-044[2]-031[2]-031[2]-007[2]-009[2]
227-216[2]-119[3]-044[2]-031[2]-033[2]-007[2]-009[2]
227-216[2]-119[3]-044[2]-034[2]-007[2]-007[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-006[2]-007[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-006[2]-008[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-026[2]-007[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-026[2]-036[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-027[2]-007[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-027[2]-037[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-028[2]-007[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-028[2]-040[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-028[2]-041[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-035[2]-008[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-035[2]-036[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-035[2]-037[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-035[2]-045[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-035[2]-046[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-038[2]-008[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-038[2]-040[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-038[2]-046[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-039[2]-007[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-039[2]-008[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-039[2]-041[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-039[2]-045[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-039[2]-046[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-042[2]-008[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-042[2]-036[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-042[2]-037[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-042[2]-040[2]-009[2]
227-216[2]-119[3]-115[2]-025[2]-042[2]-041[2]-009[2]
227-216[2]-119[3]-115[2]-111[2]-035[2]-008[2]-009[2]
227-216[2]-119[3]-115[2]-111[2]-035[2]-036[2]-009[2]
227-216[2]-119[3]-115[2]-111[2]-035[2]-037[2]-009[2]
227-216[2]-119[3]-115[2]-111[2]-035[2]-045[2]-009[2]
227-216[2]-119[3]-115[2]-111[2]-035[2]-046[2]-009[2]
227-216[2]-119[3]-115[2]-111[2]-112[2]-037[2]-009[2]
227-216[2]-119[3]-115[2]-111[2]-120[2]-045[2]-009[2]
227-216[2]-119[3]-115[2]-113[2]-035[2]-008[2]-009[2]
227-216[2]-119[3]-115[2]-113[2]-035[2]-036[2]-009[2]
227-216[2]-119[3]-115[2]-113[2]-035[2]-037[2]-009[2]
227-216[2]-119[3]-115[2]-113[2]-035[2]-045[2]-009[2]
227-216[2]-119[3]-115[2]-113[2]-035[2]-046[2]-009[2]
227-216[2]-119[3]-115[2]-113[2]-114[2]-037[2]-009[2]
227-216[2]-119[3]-115[2]-116[2]-027[2]-007[2]-009[2]
227-216[2]-119[3]-115[2]-116[2]-027[2]-037[2]-009[2]
227-216[2]-119[3]-115[2]-116[2]-112[2]-037[2]-009[2]
227-216[2]-119[3]-115[2]-116[2]-114[2]-037[2]-009[2]
227-216[2]-119[3]-115[2]-121[2]-042[2]-008[2]-009[2]
227-216[2]-119[3]-115[2]-121[2]-042[2]-036[2]-009[2]
227-216[2]-119[3]-115[2]-121[2]-042[2]-037[2]-009[2]
227-216[2]-119[3]-115[2]-121[2]-042[2]-040[2]-009[2]
227-216[2]-119[3]-115[2]-121[2]-042[2]-041[2]-009[2]
227-216[2]-119[3]-115[2]-121[2]-112[2]-037[2]-009[2]
227-216[2]-119[3]-115[2]-121[2]-114[2]-037[2]-009[2]
227-216[2]-119[3]-118[2]-034[2]-007[2]-007[2]-009[2]
227-216[2]-160[4]-008[3]-006[2]-007[2]-009[2]
227-216[2]-160[4]-008[3]-006[2]-008[2]-009[2]
227-216[2]-160[4]-008[3]-007[2]-007[2]-009[2]
227-216[2]-160[4]-008[3]-008[2]-007[2]-009[2]
227-216[2]-160[4]-008[3]-008[2]-008[2]-009[2]
227-216[2]-160[4]-008[3]-009[2]-007[2]-009[2]
227-216[2]-160[4]-160[2]-008[3]-007[2]-009[2]
227-216[2]-160[4]-160[2]-008[3]-008[2]-009[2]
227-216[2]-160[4]-160[2]-160[2]-008[3]-009[2]
227-216[2]-160[4]-160[2]-160[2]-161[2]-009[3]
227-216[2]-160[4]-161[2]-009[3]-007[2]-009[2]
227-216[2]-160[4]-161[2]-161[4]-009[3]
227-216[2]-160[4]-160[4]-008[3]-009[2]
227-216[2]-160[4]-160[4]-161[2]-009[3]
227-216[2]-215[4]-111[3]-035[2]-008[2]-009[2]
227-216[2]-215[4]-111[3]-035[2]-036[2]-009[2]
227-216[2]-215[4]-111[3]-035[2]-037[2]-009[2]
227-216[2]-215[4]-111[3]-035[2]-045[2]-009[2]
227-216[2]-215[4]-111[3]-035[2]-046[2]-009[2]
227-216[2]-215[4]-111[3]-112[2]-037[2]-009[2]
227-216[2]-215[4]-111[3]-120[2]-045[2]-009[2]
227-216[2]-215[4]-160[4]-008[3]-009[2]
227-216[2]-215[4]-160[4]-161[2]-009[3]
227-216[2]-215[4]-219[2]-120[3]-045[2]-009[2]
227-216[2]-215[4]-219[2]-161[4]-009[3]

Filed in BCS, Coding, php | No Comments »

Coordination Numbers

September 3, 2009 Posted by Emre S. Tasci

Recently, we are working on liquid alloys and for our work, we need the coordination number distribution. It’s kind of a gray area when you talk about coordination number of atoms in a liquid but it’s better than nothing to understand the properties and even more. I’d like to write a log on the tools I’ve recently coded/used in order to refer to in the future if a similar situation occurs. Also, maybe there are some others conducting similar research so, the tools introduced here may be helpful to them.

Recently, while searching recent publications on liquid alloys, I’ve found a very good and resourceful article on liquid Na-K alloys by Dr. J.-F. Wax (“Molecular dynamics study of the static structure of liquid Na-K alloys”, Physica B 403 (2008) 4241-48 | doi:10.1016/j.physb.2008.09.014). In this paper, among other properties, he had also presented the partial pair distribution functions. Partial-pair distribution functions is the averaged probability that you’ll encounter an atom in r distance starting from another atom. In solid phase, due to the symmetry of the crystal structure, you have discrete values instead of a continuous distribution and everything is crystal clear but I guess that’s the price we pay dealing with liquids. 8)

Partial-pair distribution functions are very useful in the sense that they let you derive the bond-length between constituent atom species, corresponding to the first minimums of the plots. Hence, one can see the neighborhood ranges by just looking at the plots.

I’ve sent a mail to Dr. Wax explaining my research topics and my interest and asking for his research data to which he very kindly and generously replied by providing his data.

He had sent me a big file with numerous configurations (coordinates of the atoms) following each other. The first -and the simplest- task was to split the file into seperate configuration files via this bash script:

#!/bin/bash
# Script Name: split_POS4.sh
# Splits the NaK conf files compilation POS4_DAT into sepearate
# conf files.
# Emre S. Tasci <e.tasci@tudelft.nl>
#                                              01/09/09

linestart=2
p="p"
for (( i = 1; i <= 1000; i++ ))
do
    echo $i;
    lineend=$(expr $linestart + 2047)
    confname=$(printf "%04d" $i)
    echo -e "3\n2048" > $confname
    sed -n "$linestart,$(echo $lineend$p)" POS4_DAT >> $confname
    linestart=$(expr $lineend + 1)
    cat $confname | qhull i TO $confname.hull
done

(The compilation was of 1000 configurations, each with 2048 atoms)

As you can check in the line before the “done” closer, I’ve -proudly- used Qhull software to calculate the convex hull of each configuration. A convex hull is the -hopefully minimum- shape that covers all your system. So, for each configuration I now had 2 files: “xxxx” (where xxxx is the id/number of the configuration set) storing the coordinates (preceded by 3 and 2048, corresponding to dimension and number of atoms information for the qhull to parse & process) and “xxxx.hull” file, generated by the qhull, containing the vertices list of each facet (preceded by the total number of facets).

A facet is (in 3D) the plane formed by the vertice points. Imagine a cube, where an atom lies at each corner, 3 in the inside. So, we can say that our system consists of 11 atoms and the minimal shape that has edges selected from system’s atoms and covering the whole is a cube, with the edges being the 8 atoms at the corners. Now, add an atom floating over the face at the top. Now the convex hull that wraps our new system would no longer be a 6-faced, 8-edged cube but a 9-faced, 9-edged polygon. I need to know the convex hull geometry in order to correctly calculate the coordination number distributions (details will follow shortly).

The aforementioned two files look like:

sururi@husniya hull_calcs $ head 0001
3
2048
 0.95278770E+00 0.13334565E+02 0.13376155E+02
 0.13025256E+02 0.87618381E+00 0.20168993E+01
 0.12745038E+01 0.14068998E-01 0.22887323E+01
 0.13066590E+02 0.20788591E+01 0.58119183E+01
 0.10468218E+00 0.58523640E-01 0.64288678E+01
 0.12839412E+02 0.13117012E+02 0.79093881E+01
 0.11918105E+01 0.12163854E+02 0.10270868E+02
 0.12673985E+02 0.11642538E+02 0.10514597E+02
sururi@husniya hull_calcs $ head 0001.hull
180
568 1127 1776
1992 104 1551
956 449 1026
632 391 1026
391 632 1543
391 956 1026
966 632 1026
966 15 1039
632 966 1039

The sets of 3 numbers in the xxxx.hull file is the ids/numbers of the atoms forming the edges of the facets, i.e., they are the vertices.

To calculate the coordination number distribution, you need to pick each atom and then simply count the other atoms within the cut-off distance depending on your atom’s and the neighboring atom’s species. After you do the counting for every atom, you average the results and voilÃ ! there is your CN distribution. But here’s the catch: In order to be able to count properly, you must make sure that, your reference atom’s cutoff radii stay within your system — otherwise you’ll be undercounting. Suppose your reference atom is one of the atoms at the corners of the cube: It will (generally/approximately) lack 7/8 of the neighbouring atoms it would normally have if it was to be the center atom of the specimen/sample. Remember that we are studying a continuous liquid and trying to model the system via ensembles of samples. So we should omit these atoms which has neighborhoods outside of our systems. Since neighborhoods are defined through bond-length, we should only include the atoms with a distance to the outside of at least cut-off radii. The “outside” is defined as the region outside the convex hull and it’s designated by the facets (planes).

From the xxxx.hull file, we have the ids of the vertice atoms and their coordinates are stored in the xxxx file. To define the plane equation

we will use the three vertice points, say p1, p2 and p3. From these 3 points, we calculate the normal n as:
$\vec{n}=\left(\vec{p_2}-\vec{p_1}\right)\times\left(\vec{p_3}-\vec{p_1}\right)$
then, the plane equation (hence the coefficients a,b,c,d) can be derived by comparing the following equation:
$n_{x}\left(x-x_{0} \right)+n_{y}\left(y-y_{0} \right)+n_{z}\left(z-z_{0} \right) = 0$
Here, (x0,y0,z0) are just the coordinates of any of the vertice points. And finally, the distance D between a point p1(x1,y1,z1) and a plane (a,b,c,d) is given by:
$D=\frac{\left|ax_{1}+by_{1}+cz_{1} \right|}{\sqrt[]{a^{2}+b^{2}+c^{2}}}$

Since vector operations are involved, I thought it’s better to do this job in Octave and wrote the following script that calculates the coefficients of the facets and then sets down to find out the points whose distances to all the facets are greater than the given cut-off radius:

sururi@husniya trunk $ cat octave_find_atoms_within.m
DummyA = 3;
%conf_index=292;

% Call from the command line like :
%   octave -q --eval "Rcut=1.65;conf_index=293;path='$(pwd)';" octave_find_atoms_within.m
% hence specifying the conf_index at the command line.

% Emre S. Tasci <e.tasci@tudelft.nl>                    *
%
% From the positions and vertices file, calculates the plane
% equations (stored in "facet_coefficients") and then
% filters the atoms with respect to their distances to these
% facets. Writes the output to
% "hull_calcs/xxxx_insiders.txt" file
%                                              03/09/09 */

conf_index_name = num2str(sprintf("%04d",conf_index));;
%clock
clear facet_coefficients;
facet_coefficients = [];
global p v facet_coefficients
fp = fopen(strcat(path,"/hull_calcs/",conf_index_name));
k = fscanf(fp,"%d",2); % 1st is dim (=3), 2nd is number of atoms (=2048)
p = fscanf(fp,"%f",[k(1),k(2)]);
p = p';
fclose(fp);
%p = load("/tmp/del/delco");
fp = fopen(strcat(path,"/hull_calcs/",conf_index_name,".hull"));
k = fscanf(fp,"%d",1);% number of facets
v = fscanf(fp,"%d",[3,k]);
v = v';
fclose(fp);
%v = load("/tmp/del/delver");

function [a,b,c,d,e] = getPlaneCoefficients(facet_index)
    global p v
    % Get the 3 vertices
    p1 = p(v(facet_index,1)+1,:); % The +1s come from the fact 
    p2 = p(v(facet_index,2)+1,:); % that qhull enumeration begins
    p3 = p(v(facet_index,3)+1,:); % from 0 while Octave's from 1

    %printf("%d: %f %f %f %f %f %f %f %f %f\n",facet_index,p1,p2,p3);

    % Calculate the normal
    n = cross((p2-p1),(p3-p1));

    % Calculate the coefficients of the plane :
    % ax + by + cz +d = 0
    a = n(1);
    b = n(2);
    c = n(3);
    d = -(dot(n,p1));
    e = norm(n);
    if(e==0)
        printf("%f\n",p1);
        printf("%f\n",p2);
        printf("%f\n",p3);
        printf("%d\n",facet_index);
    endif
endfunction

function dist = distanceToPlane(point_index,facet_index)
    global p facet_coefficients
    k = facet_coefficients(facet_index,:);
    n = [k(1) k(2) k(3)];
    dist = abs(dot(n,p(point_index,:)) + k(4)) / k(5);
endfunction

for i = [1:size(v)(1)]
    [a,b,c,d,e] = getPlaneCoefficients(i);
    facet_coefficients = [ facet_coefficients ; [a,b,c,d,e]];
endfor

%Rcut = 1.65; % Defined from command line calling
% Find the points that are not closer than Rcut
inside_atoms = [];
for point = [1:size(p)(1)]
%for point = [1:100]
    inside=true;
    for facet = [1:size(v)(1)]
    %for facet = [1:10]
        %printf("%d - %d : %f\n",point,facet,dist);
        if (distanceToPlane(point,facet)<Rcut)
            inside = false;
            break;
        endif
    endfor
    if(inside)
        inside_atoms = [inside_atoms point-1];
    endif
endfor

fp = fopen(strcat(path,"/hull_calcs/",conf_index_name,"_insiders.txt"),"w");
fprintf(fp,"%d\n",inside_atoms);
fclose(fp);
%clock

This script is runned within the following php code which then takes the filtered atoms and does the counting using them:

<?PHP
/* Emre S. Tasci <e.tasci@tudelft.nl>                    *
 *
 * parse_configuration_data.php
 *
 * Written in order to parse the configuation files
 * obtained from J.F. Wax in order to calculate the 
 * Coordination Number distribution. Each configuration 
 * file contain 2048 atoms' coordinates starting at the 
 * 3rd line. There is also a convex hull file generated 
 * using qhull (http://www.qhull.com) that contains the 
 * indexes (starting from 0) of the atoms that form the 
 * vertices of the convex hull. Finally there is the 
 * IP.dat file that identifies each atom (-1 for K; 1 for 
 * Na -- the second column is the relative masses).
 *
 *                                              02/09/09 */

/*
# if present, remove the previous run's results file
if(file_exists("results.txt"))
    unlink("results.txt");
 */

error_reporting(E_ALL ^ E_NOTICE);

if(!file_exists("results.txt"))
{
    $fp = fopen("results.txt","w");
    fwrite($fp,"CONF#"."\tNa".implode("\tNa",range(1,20))."\tK".implode("\tK",range(1,20))."\n");
    fclose($fp);
}

# Support for command line variable passing:
for($i=1;$i<sizeof($_SERVER["argv"]);$i++)
{
        list($var0,$val0) = explode("=",$_SERVER["argv"][$i]);
        $_GET[$var0] = $val0;
}

if($_GET["configuration"])
    calculate($_GET["configuration"]);
else
    exit("Please specify a configuration number [php parse_configuration_data.php configuration=xxx]\n");

function calculate($conf_index)
{
    # Define the atoms array
    $arr_atoms = Array();

    # Get the information from the files
    parse_types($arr_atoms);
    $refs = get_vertices($conf_index);
    parse_coordinates($arr_atoms,$conf_index);

    # Define the Rcut-off values (obtained from partial parid distribution minimums)
    $Rcut_arr = Array();
    $Rscale = 3.828; # To convert reduced distances to Angstrom (if needed)
    $Rscale = 1; # To convert reduced distances to Angstrom
    $Rcut_arr["Na"]["Na"] = 1.38 * $Rscale;
    $Rcut_arr["Na"]["K"]  = 1.65 * $Rscale;
    $Rcut_arr["K"]["Na"]  = 1.65 * $Rscale;
    $Rcut_arr["K"]["K"]   = 1.52 * $Rscale;
    $Rcut = $Rcut_arr["Na"]["K"]; # Taking the maximum one as the Rcut for safety

    /*
    # We have everything we need, so proceed to check 
    # if an atom is at safe distance wrt to the vertices

    # Define all the ids
    $arr_test_ids = range(0,2047);
    # Subtract the ref atoms' ids
    $arr_test_ids = array_diff($arr_test_ids, $refs);
    sort($arr_test_ids);
    //print_r($arr_test_ids);

    $arr_passed_atom_ids = Array();
    # Check each atom against refs
    for($id=0, $size=sizeof($arr_test_ids); $id<$size; $id++)
    {
        //echo $id."\n";
        $arr_atoms[$arr_test_ids[$id]]["in"] = TRUE;
        foreach ($refs as $ref)
        {
            $distance = distance($arr_atoms[$arr_test_ids[$id]],$arr_atoms[$ref]);
            //echo "\t".$ref."\t".$distance."\n";
            if($distance < $Rcut)
            {
                $arr_atoms[$arr_test_ids[$id]]["in"] = FALSE;
                break;
            }
        }
        if($arr_atoms[$arr_test_ids[$id]]["in"] == TRUE)
            $arr_passed_atom_ids[] = $arr_test_ids[$id];
    }
     */

    # Run the octave script file to calculate the inside atoms
    if(!file_exists("hull_calcs/".sprintf("%04d",$conf_index)."_insiders.txt"))
    exec("octave -q --eval \"Rcut=".$Rcut.";conf_index=".$conf_index.";path='$(pwd)';\" octave_find_atoms_within.m");

    # Read the file generated by Octave
    $arr_passed_atom_ids = file("hull_calcs/".sprintf("%04d",$conf_index)."_insiders.txt",FILE_IGNORE_NEW_LINES);

    $arr_test_ids = range(0,2047);
    $arr_test_ids = array_diff($arr_test_ids, $refs);
    sort($arr_test_ids);
    for($i=0, $size=sizeof($arr_test_ids);$i<$size;$i++)
        $arr_atoms[$arr_test_ids[$i]]["in"]=FALSE;

    # Begin checking every passed atom
    foreach($arr_passed_atom_ids as $passed_atom_id)
    {
        $arr_atoms[$passed_atom_id]["in"] = TRUE;
        for($i=0, $size=sizeof($arr_atoms); $i<$size; $i++)
        {
            $distance = distance($arr_atoms[$passed_atom_id],$arr_atoms[$i]);
            //echo $passed_atom_id."\t---\t".$i."\n";
            if($distance < $Rcut_arr[$arr_atoms[$passed_atom_id]["id"]][$arr_atoms[$i]["id"]] && $distance>0.001)
                $arr_atoms[$passed_atom_id]["neighbour_count"] += 1;
        }
    }

    # Do the binning
    $CN_Na = Array();
    $CN_K  = Array();
    for($i=0, $size=sizeof($arr_atoms); $i<$size; $i++)
    {
        if(array_key_exists("neighbour_count",$arr_atoms[$i]))
        {
            ${"CN_".$arr_atoms[$i]['id']}[$arr_atoms[$i]["neighbour_count"]] += 1;
        }
    }

    ksort($CN_Na);
    ksort($CN_K);

    //print_r($arr_atoms);
    //print_r($CN_Na);
    //print_r($CN_K);

    # Report the results
    $filename = "results/".sprintf("%04d",$conf_index)."_results.txt";
    $fp = fopen($filename,"w");
    fwrite($fp, "### Atoms array ###\n");
    fwrite($fp,var_export($arr_atoms,TRUE)."\n");
    fwrite($fp, "\n### CN Distribution for Na ###\n");
    fwrite($fp,var_export($CN_Na,TRUE)."\n");
    fwrite($fp, "\n### CN Distribution for K ###\n");
    fwrite($fp,var_export($CN_K,TRUE)."\n");

    # Percentage calculation:
    $sum_Na = array_sum($CN_Na);
    $sum_K  = array_sum($CN_K);
    foreach($CN_Na as $key=>$value)
        $CN_Na[$key] = $value * 100 / $sum_Na;
    foreach($CN_K  as $key=>$value)
        $CN_K[$key]  = $value * 100 / $sum_K;
    //print_r($CN_Na);
    //print_r($CN_K);
    fwrite($fp, "\n### CN Distribution (Percentage) for Na ###\n");
    fwrite($fp,var_export($CN_Na,TRUE)."\n");
    fwrite($fp, "\n### CN Distribution (Percentage) for K ###\n");
    fwrite($fp,var_export($CN_K,TRUE)."\n");
    fclose($fp);

    # Write the summary to the results file
    $fp = fopen("results.txt","a");
    for($i=1;$i<=20;$i++)
    {
        if(!array_key_exists($i,$CN_Na))
            $CN_Na[$i] = 0;
        if(!array_key_exists($i,$CN_K))
            $CN_K[$i] = 0;
    }
    ksort($CN_Na);
    ksort($CN_K);
    fwrite($fp,sprintf("%04d",$conf_index)."\t".implode("\t",$CN_Na)."\t".implode("\t",$CN_K)."\n");
    fclose($fp);

}

function parse_types(&$arr_atoms)
{
    # Parse the types
    $i = 0;
    $fp = fopen("IP.DAT", "r");
    while(!feof($fp))
    {
        $line = fgets($fp,4096);
        $auxarr = explode(" ",$line);
        if($auxarr[0]==-1)
            $arr_atoms[$i]["id"] = "Na";
        else
            $arr_atoms[$i]["id"] = "K";
        $i++;
    }
    fclose($fp);
    array_pop($arr_atoms);
    return 0;
}

function get_vertices($conf_index)
{
    $arr_refs = Array();

    # Get the ids of the vertices of the convex hull
    $filename = "hull_calcs/".sprintf("%04d",$conf_index).".hull";
    $fp = fopen($filename, "r");

    # Bypass the first line
    $line = fgets($fp,4096);

    while(!feof($fp))
    {
        $line = fgets($fp,4096);
        $auxarr = explode(" ",$line);
        array_pop($auxarr);
        $arr_refs = array_merge($arr_refs, $auxarr);
    }
    fclose($fp);
    // $arr_refs = array_unique($arr_refs); # This doesn't lose the keys
    $arr_refs = array_keys(array_count_values($arr_refs)); # But this does.
    return $arr_refs;
}

function parse_coordinates(&$arr_atoms, $conf_index)
{
    # Parse the coordinates
    $i = 0;
    $filename = "hull_calcs/".sprintf("%04d",$conf_index);
    $fp = fopen($filename, "r");

    # Bypass the first two lines
    $line = fgets($fp,4096);
    $line = fgets($fp,4096);

    while(!feof($fp))
    {
        $line = fgets($fp,4096);
        $arr_atoms[$i]["coords"] = explode(" ",$line);
        array_shift($arr_atoms[$i]["coords"]);
        $i++;
    }
    fclose($fp);
    array_pop($arr_atoms);
    return 0;
}

function distance(&$atom1,&$atom2)
{
    # Calculate the distance between the two atoms
    $x1 = $atom1["coords"][0];
    $x2 = $atom2["coords"][0];
    $y1 = $atom1["coords"][1];
    $y2 = $atom2["coords"][1];
    $z1 = $atom1["coords"][2];
    $z2 = $atom2["coords"][2];
    return sqrt(pow($x1-$x2,2) + pow($y1-$y2,2) + pow($z1-$z2,2));
}

?>

The code above generates a “results/xxxx_results.txt” file containing all the information obtained in arrays format and also appends to “results.txt” file the relevant configuration file’s CN distribution summary. The systems can be visualized using the output generated by the following plotter.php script:

<?PHP
/* Emre S. Tasci <e.tasci@tudelft.nl>                    *
 * Parses the results/xxxx_results.txt file and generates 
 * an XYZ file such that the atoms are labeled as the 
 * vertice atoms, close-vertice atoms and inside atoms..
 *                                              02/09/09 */

# Support for command line variable passing:
for($i=1;$i<sizeof($_SERVER["argv"]);$i++)
{
        list($var0,$val0) = explode("=",$_SERVER["argv"][$i]);
        $_GET[$var0] = $val0;
}

if($_GET["configuration"])
    $conf_index = $_GET["configuration"];
else 
    exit("Please specify a configuration number [php plotter.php configuration=xxx]\n");

$filename = sprintf("%04d",$conf_index);

# Get the atom array from the results file. Since results file 
# contains other arrays as well, we slice the file using sed for the 
# relevant part
$last_arr_line = exec('grep "### CN Distribution" results/'.$filename.'_results.txt -n -m1|sed "s:^\([0-9]\+\).*:\1:gi"');
exec('sed -n "2,'.($last_arr_line-1).'p" results/'.$filename.'_results.txt > system_tmp_array_dump_file');
$str=file_get_contents('system_tmp_array_dump_file');
$atom_arr=eval('return '.$str.';');
unlink('system_tmp_array_dump_file');

# Now that we have the coordinates, we itarate over the atoms to check 
# the characteristic and designate them in the XYZ file.
$fp = fopen("system_".$filename.".xyz","w");
fwrite($fp,sizeof($atom_arr)."\n");
fwrite($fp,"Generated by plotter.php\n");
for($i=0, $size=sizeof($atom_arr);$i<$size;$i++)
{
    if(!array_key_exists("in",$atom_arr[$i]))
        $atomlabel = "Mg";#Vertices
    elseif($atom_arr[$i]["in"]==TRUE)
        $atomlabel = $atom_arr[$i]["id"];#Inside atoms
    else
        $atomlabel = "O";#Close-vertice atoms
    fwrite($fp,$atomlabel."\t".implode("\t",$atom_arr[$i]["coords"]));
}
fclose($fp);
?>

which generates a “system_xxxx.xyz” file, ready to be viewed in a standard molecule viewing software. It designates the vertice atoms (of the convex hull, remember? 8)as “Mg” and the atoms close to them as “O” for easy-viewing purpose. A sample parsed file looks like this:

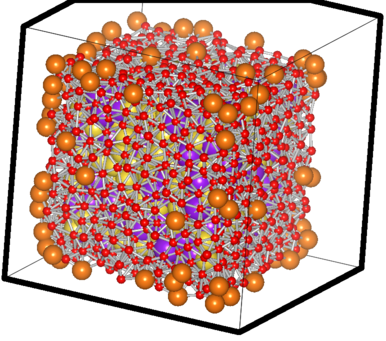
The filtered case of a sample Na-K system

The big orange atoms are the omitted vertice atoms; the small red ones are the atoms critically close to the facets and hence also omitted ones. You can see the purple and yellow atoms which have passed the test sitting happilly inside, with the counting done using them.. 8)

Filed in Coding, Definition & Method, Octave, php, Physics, Tools | No Comments »

POSCAR2Cif with symmetries discovered

June 4, 2009 Posted by Emre S. Tasci

In previous posts, I had submitted two codes:

POSCAR2Cif : that converts a given POSCAR file to CIF, so to speak, ruthlessly, i.e. just as is, without checking for symmetries or anything.
POSCAR2findsymm : another converter that takes a POSCAR file, and prepares an input file such that Harold Stokes’ findsym code from the ISOTROPY package would proceed it and deduce the symmetry information. If findsym executable is not accessible in your system (or if you run the script with the “t” flag set to on), it would just print the input to the screen and you could use it to fill the input form of the code’s web implementation, instead

Anyway, recently it occured to me to write another script that would parse the output of the POSCAR2findsymm output and use that output to construct a CIF file that contained the equivalent sites, etc.. So, ladies and gentlemen, here it is (drums roll)…

Example: Code in action
Using the same POSCAR_Pd3S file as in the POSCAR2Cif entry… Feeding it to POSCAR2findsymm and then applying findsymm2cif on it

sururi@husniya tmp $ python /code/POSCAR2findsym/POSCAR2findsym.py POSCAR_Pd3S | php /code/vaspie/findsymm2cif.php speclist=Pd,S
_cell_length_a  7.21915
_cell_length_b  5.56683
_cell_length_c  7.68685
_cell_angle_alpha       90.00000
_cell_angle_beta        90.00000
_cell_angle_gamma       90.00000
_symmetry_Int_Tables_number     40

loop_
_atom_site_label
_atom_site_type_symbol
_atom_site_fract_x
_atom_site_fract_y
_atom_site_fract_z
Pd01    Pd       0.75000         0.17834         0.31139
Pd02    Pd       0.75000         0.17845         0.69126
Pd03    Pd       0.50000         0.00000         0.00132
S01     S        0.75000         0.81592         0.50152

Code

#!/usr/bin/php
<?PHP

//require("/code/toolbox/commandline.inc.php"); # Equivalent handling of $_GET / $_POST
# ============/code/toolbox/commandline.inc.php========================================
// Enables the same treat for command line parameters
// as those of GET parameters.
// Also sets the $first, $last ranges including the gall parameter
 
//Support for command line variable passing:
for($i=1;$i<sizeof($_SERVER["argv"]);$i++)
{
  list($var0,$val0) = explode("=",$_SERVER["argv"][$i]);
  $_GET[$var0] = $val0;
}
 
# ============/code/toolbox/commandline.inc.php========================================
if($_GET["h"]||$_GET["help"])
{
$help = <<<lol
 * Script name: findsymmetry2cif.php                                *
 * Converts the specified FINDSYM output to CIF format              *
 * More Information on FINDSYM : http://stokes.byu.edu/findsym.html *
 *                                                                  *
 * (If you have access) More information on script:                 *
 * http://dutsm2017.stm.tudelft.nl/mediawiki/index.php?title=Findsymm2cif
 *                                                                  *
 * Emre S. Tasci <e.tasci@tudelft.nl>                               *
 *                                                        23/05/09  *

 Usage:
 f         : input file  (Default = stdin)
 o         : output file (Default = stdout)
 identical : if set (identical=1), then the output will be the 
             transformation matrix and origin shift applied to the coordinates 
             so that the given coordinates will be regained.
 speclist  : Define the name of the species, seperated by 'xx' or ',' to be used
             with neighbour listing (Default = AxxBxxCxx...)
             (Labels can also be seperated via [space] as long as speclist is given
             in quotation -- Example: ... speclist=\"Au Si\" )

 Example : php findsymmetry2cif.php f=POSCAR_RhBi4 speclist=Bi,Rh identical=1
lol;
 echo $help."\n";
 exit;
}

$input = "php://stdin";
if($_GET["f"]) $input=$_GET["f"];

$outfile = "php://stdout";
if($_GET["o"]) $outfile=$_GET["o"];

$species_type_template = Array("A","B","C","D","E","F","G","H","I","J","K","L","M","N","O","P","Q","R","S","T","U","V","W","X","Y","Z");
if($_GET["speclist"])$species_type_template = split("xx| |,",$_GET["speclist"]);

//if(file_exists("findsymm2cif_php.tmp"))
//    unlink("findsymm2cif_php.tmp");
if($input == "php://stdin")
{
    $lol = file("php://stdin");
    $fp1 = fopen("findsymm2cif_php2.tmp","w");
    foreach($lol as $line)
        fwrite($fp1,$line);
    fclose($fp1);
    $input = "findsymm2cif_php2.tmp";
}
exec('lstart=`grep -n "Type of each atom:" '.$input.'|sed "s:^\([0-9]\+\).*:\1:gi"`;lstart=`expr $lstart + 1`;lfinish=`grep -n "Position of each atom (dimensionless coordinates)" '.$input.'|sed "s:^\([0-9]\+\).*:\1:gi"`;lfinish=`expr $lfinish - 1`;cat '.$input.' |sed -n "`echo $lstart`,`echo $lfinish`p" | sed \':a;N;$!ba;s/\n/ /g\' > findsymm2cif_php.tmp');
exec('grep "Number of atoms in unit cell:" '.$input.' -A1 | tail -n1  >> findsymm2cif_php.tmp');
exec('grep "Space Group" '.$input.' | awk \'{print $3}\'  >> findsymm2cif_php.tmp');
exec('grep "Origin at" '.$input.' | awk \'{print $3 "\t" $4 "\t" $5}\'  >> findsymm2cif_php.tmp');
exec('grep "Vectors a,b,c:" '.$input.' -A3 | tail -n3  >> findsymm2cif_php.tmp');
exec('grep "Values of a,b,c,alpha,beta,gamma:" '.$input.' -A1 | tail -n1  >> findsymm2cif_php.tmp');
exec('grep "Wyckoff" '.$input.' -A1 -n | grep "^[0-9]\+-[0-9]"| sed "s:\(^[0-9]\+\)-[0-9]\+\(.*\):\1\t\2:gi" >> findsymm2cif_php.tmp');

if($input == "findsymm2cif_php2.tmp")
{
    $input = "php://stdin";
    //unlink("findsymm2cif_php2.tmp");
}

//exec("sh findsymm2cif.sh findsymm.out",$file);

$file = file("findsymm2cif_php.tmp");
$type_atoms = split("[ \t]+",trim($file[0]));
$specie_count = Array();
$k = 0;
$specie_count[$k] = 1;
for($i=1; $i < sizeof($type_atoms); $i++)
{
    if($type_atoms[$i] != $type_atoms[$i-1])
        $k++;
    $specie_count[$k]++;
}
for($i=1; $i<sizeof($specie_count); $i++)
    $specie_count[$i] += $specie_count[$i-1];
//print_r($specie_count);

$numatoms = trim($file[1]);
$sgno = trim($file[2]);
$origin_shift = split("[ \t]+",trim($file[3]));
$tr_x = split("[ \t]+",trim($file[4]));
$tr_y = split("[ \t]+",trim($file[5]));
$tr_z = split("[ \t]+",trim($file[6]));
$params = split("[ \t]+",trim($file[7]));
$specie = Array();
for($i = 8;$i<sizeof($file);$i++)
    $specie[] = split("[ \t]+",trim($file[$i]));
$totatoms = 0;
for($i = 0; $i < sizeof($specie)-1; $i++)
{
    $specie[$i][0] = $specie[$i+1][0] - $specie[$i][0] - 1;
    $totatoms += $specie[$i][0];
}
$specie[sizeof($specie)-1][0] = $numatoms - $totatoms;
//print_r($specie);
//print_r($specie_count);
$atoms_counted = 0;
for($i = 0; $i < sizeof($specie); $i++)
{
    # Going over atoms
    $atoms_counted += $specie[$i][0];
    for($j = 0; $j<sizeof($specie_count); $j++)
    {
        if($atoms_counted <= $specie_count[$j])
        {
            $specie[$i][0] = $species_type_template[$j];
            break;
        }
    }
}
//print_r($specie);

if($_GET["identical"])
{
    # Calculate the atom positions corresponding with the given POSCAR
    $trmatrix=Array();
    $trmatrix[0][0] = $tr_x[0];
    $trmatrix[0][1] = $tr_x[1];
    $trmatrix[0][2] = $tr_x[2];
    $trmatrix[1][0] = $tr_y[0];
    $trmatrix[1][1] = $tr_y[1];
    $trmatrix[1][2] = $tr_y[2];
    $trmatrix[2][0] = $tr_z[0];
    $trmatrix[2][1] = $tr_z[1];
    $trmatrix[2][2] = $tr_z[2];

    for($i=0;$i < sizeof($specie); $i++)
    {
        $x = $specie[$i][1];
        $y = $specie[$i][2];
        $z = $specie[$i][3];
        
        $xx = $x*$trmatrix[0][0] + $y*$trmatrix[1][0] + $z*$trmatrix[2][0];
        $yy = $x*$trmatrix[0][1] + $y*$trmatrix[1][1] + $z*$trmatrix[2][1];
        $zz = $x*$trmatrix[0][2] + $y*$trmatrix[1][2] + $z*$trmatrix[2][2];

        $xx += $origin_shift[0];
        $yy += $origin_shift[1];
        $zz += $origin_shift[2];

        $specie[$i][1] = $xx;
        $specie[$i][2] = $yy;
        $specie[$i][3] = $zz;

        for($j=1;$j<4;$j++)
        {
            while($specie[$i][$j]>=1.0)
                $specie[$i][$j]-=1.0;
            while($specie[$i][$j]<0.0)
                $specie[$i][$j]+=1.0;
        }

    }
}

$fp = fopen($outfile,"w");
fwrite($fp,"_cell_length_a"."\t".$params[0]."\n");
fwrite($fp,"_cell_length_b"."\t".$params[1]."\n");
fwrite($fp,"_cell_length_c"."\t".$params[2]."\n");
fwrite($fp,"_cell_angle_alpha"."\t".$params[3]."\n");
fwrite($fp,"_cell_angle_beta"."\t".$params[4]."\n");
fwrite($fp,"_cell_angle_gamma"."\t".$params[5]."\n");
fwrite($fp,"_symmetry_Int_Tables_number"."\t".$sgno."\n\n");
fwrite($fp, "loop_\n_atom_site_label\n_atom_site_type_symbol\n_atom_site_fract_x\n_atom_site_fract_y\n_atom_site_fract_z\n");
//print_r ($specie);
$k = 0;
$specie_type = $specie[0][0];
for($i=0;$i<sizeof($specie);$i++)
{
    if($specie[$i][0] == $specie_type)
        $k++;
    else
    {
        $k = 1;
        $specie_type = $specie[$i][0];
    }
    fwrite($fp, $specie[$i][0].sprintf("%02d",$k)."\t".$specie[$i][0]."\t".sprintf("%8.5f",$specie[$i][1])."\t".sprintf("%8.5f",$specie[$i][2])."\t".sprintf("%8.5f",$specie[$i][3])."\n");
}
fclose($fp);
?>

Filed in Coding, php, Tools | No Comments »

Some unit cell functions for Octave

May 23, 2009 Posted by Emre S. Tasci

I’ve written some functions to aid in checking the transformations as well as switching between the parameter â vector representations.

latpar2vec([a,b,c,alpha,beta,gamma])
Given the a,b,c,Î±,Î² and Î³, the function calculates the lattice vectors

function f=latpar2vec(X)
% function f=latpar2vec([a,b,c,alpha,beta,gamma])
% Calculates the lattice vectors from the given lattice paramaters.
  
a     = X(1);
b     = X(2);
c     = X(3);
alpha = X(4);
beta  = X(5);
gamma = X(6);
 
% Converting the angles to radians:
alpha = d2r(alpha);
beta  = d2r(beta);
gamma = d2r(gamma);
 
%Aligning a with the x axis:
ax = a;
ay = 0;
az = 0;
 
%Orienting b to lie on the x-y plane:
bz = 0;
 
% Now we have 6 unknowns for 6 equations..
bx = b*cos(gamma);
by = (b**2-bx**2)**.5;
cx = c*cos(beta);
cy = (b*c*cos(alpha)-bx*cx)/by;
cz = (c**2-cx**2-cy**2)**.5;
f=[ax ay az
   bx by bz
   cx cy cz];
endfunction

latvec2par([ax ay az; bx by bz; cx cy cz])
Calculates the lattice parameters a,b,c,Î±,Î² and Î³ from the lattice vectors

function f=latvec2par(x)
% function f=latvec2par(x)
%     ax ay az
% x = bx by bz
%     cx cy cz
%
% takes the unit cell vectors and calculates the lattice parameters
% Emre S. Tasci <e.tasci@tudelft.nl>   03/10/08
 
av = x(1,:);
bv = x(2,:);
cv = x(3,:);
 
a = norm(av);
b = norm(bv);
c = norm(cv);
 
alpha = acos((bv*cv')/(b*c))*180/pi;
beta  = acos((av*cv')/(a*c))*180/pi;
gamma = acos((av*bv')/(a*b))*180/pi;
 
f = [a b c alpha beta gamma];
endfunction

volcell([a,b,c,A,B,G])
Calculates the volume of the cell from the given lattice parameters, which is the determinant of the matrice build from the lattice vectors.

function f=volcell(X)
% function f=volcell([a,b,c,A,B,G])
% Calculate the cell volume from lattice parameters
%
% Emre S. Tasci, 09/2008
a=X(1);
b=X(2);
c=X(3);
A=X(4); % alpha
B=X(5); % beta
G=X(6); % gamma
 f=a*b*c*(1-cos(d2r(A))^2-cos(d2r(B))^2-cos(d2r(G))^2+2*cos(d2r(A))*cos(d2r(B))*cos(d2r(G)))^.5;
endfunction

Why’s there no “volcell” function for the unit cell vectors? You’re joking, right? (det(vector)) ! 🙂

Example

octave:13> % Define the unit cell for PtSn4 :
octave:13> A = latpar2vec([ 6.41900 11.35700  6.38800  90.0000  90.0000  90.0000 ])
A =
 
    6.41900    0.00000    0.00000
    0.00000   11.35700    0.00000
    0.00000    0.00000    6.38800
 
octave:14> % Cell volume :
octave:14> Apar = [ 6.41900 11.35700  6.38800  90.0000  90.0000  90.0000 ]
Apar =
 
    6.4190   11.3570    6.3880   90.0000   90.0000   90.0000
 
octave:15> % Define the unit cell for PtSn4 :
octave:15> Apar=[ 6.41900 11.35700  6.38800  90.0000  90.0000  90.0000 ]
Apar =
 
    6.4190   11.3570    6.3880   90.0000   90.0000   90.0000
 
octave:16> % Cell volume :
octave:16> Avol = volcell (Apar)
Avol =  465.69
 
octave:17> % Calculate the lattice vectors :
octave:17> A = latpar2vec (Apar)
A =
 
    6.41900    0.00000    0.00000
    0.00000   11.35700    0.00000
    0.00000    0.00000    6.38800
 
octave:18> % Verify the volume :
octave:18> det(A)
ans =  465.69
 
octave:19> % Define the transformation matrix :
octave:19> R = [ 0 0 -1 ; -1 0 0 ; .5 .5 0]
R =
 
   0.00000   0.00000  -1.00000
  -1.00000   0.00000   0.00000
   0.50000   0.50000   0.00000
 
octave:21> % The reduced unit cell volume will be half of the original one as is evident from :
octave:21> det(R)
ans =  0.50000
 
octave:22> % Do the transformation :
octave:22> N = R*A
N =
 
  -0.00000  -0.00000  -6.38800
  -6.41900   0.00000   0.00000
   3.20950   5.67850   0.00000
 
octave:23> % The reduced cell parameters :
octave:23> Npar = latvec2par (N)
Npar =
 
     6.3880     6.4190     6.5227   119.4752    90.0000    90.0000
 
octave:24> % And the volume :
octave:24> det(N), volcell (Npar)
ans =  232.84
ans =  232.84

Filed in Coding, Octave | No Comments »

Hex, Bugs and More Physics | Emre S. Tasci

from SVN to Mercurial

August 23, 2011 Posted by Emre S. Tasci

Exploring through the paths of subgroups, collecting indexes on the way…

June 6, 2011 Posted by Emre S. Tasci

Coordination Numbers

September 3, 2009 Posted by Emre S. Tasci

POSCAR2Cif with symmetries discovered

June 4, 2009 Posted by Emre S. Tasci

Some unit cell functions for Octave

May 23, 2009 Posted by Emre S. Tasci

Categories

Archive

Blogroll

Meta

Design by