Scientific Interests
Detailed information about my academical upbringing and my advisors/mentors can be accessed from the related section of the "About Me" page, and my C.V. can be downloaded via this link. In this page, I wanted to briefly present my scientific interests (in reverse chronological order):
Application of Group Theory to Solid State Physics and Cristallography
Structural phase transitions or physical phenomena such as ferromagnetism or polarity arising from possible distortions and symmetry, can be analyzed effectively and rapidly via space groups, matrix representations of operators and group theory. Starting from the present symmetries in a system, possible interactions can be simplified to a great extent. By investigating the familarity between structures, new structures that hasn't been observed before can be predicted.
In my project within the Bilbao Crystallography Server, while developing software to automize the group theory procedures, I'm also using these very principles and procedures, to derive a method for the so-called "Barnighausen Trees" in which, possible intermediate and product structures evolved from a highly symmetryzed are predicted and classified. Thanks to the various databases contained within our server, we have a very extended area of investigation.

Scheme of the atomic displacements method for pseudosymmetry detection.
Discovery of New Materials with Novel Properties via Informatics
For a long time, scientific method consisted of theory and experiment. With the rise of the computers, an intermediate method, namely, simulation came into life. We're now at a point where the abundance of the data produced by these three methods has bestowed us the ability to employ a new tool: the Informatics. By analyzing the data about a specific topic and spotting the similarities and the patterns, candidate materials that possess the sought properties can be predicted and designed.
 "Self-healing" is an example to these sought properties: ZrO2 (Zirconia) is a material that is monoclinic at room temperature and tetragonal at highter temperatures (it transforms into cubic at even higher temperatures but this last phase isn't that relevant to our purposes). Contrary to the standard behaviour, similar to the water between 0-4 degrees C, its high temperature phase has a lower density than the low temperature phase (when heated, a relative contraction about 4% occurs accompanying the phase transition). To exploit this aspect of zirconia, Yttrium (Y) is doped at high temperatures to act as as a meta-stabilizer for the monoclinic phase at lower temperatures. Afterwards, these meta-stable zirconia particles are mixed into the ceramic where a crack formation acts as a trigger for the suspended phase transition thus causing the zirconia particles to expand. While they expand, since they condense their vicinity, the crack's progress is stopped, followed by the closing of the shear by bringing the two sides together by further pushing towards each other. Via informatics (coordination numbers of the sites in zirconia, materials that share similar transformation procedures as zirconia, perrovskites that can be related), a list of candidate materials was prepared in the hope for being alternative to zirconia and after they were subjected to various pre-filtering processes, ab-initio calculations were performed to derive equations of state in order to find possible critical pressure values. Promising candidates were further investigated for their behaviour at high temperatures with the help of the phonon theory. Eventhough two alternatives were found, due to the fact them being more expensive than zirconia, they were swept under the rug (in the meantime, there is yet another candidate, a perrovskite whom I don't want to refer by its name, waiting for its turn to be analyzed 8)
"Self-healing" is an example to these sought properties: ZrO2 (Zirconia) is a material that is monoclinic at room temperature and tetragonal at highter temperatures (it transforms into cubic at even higher temperatures but this last phase isn't that relevant to our purposes). Contrary to the standard behaviour, similar to the water between 0-4 degrees C, its high temperature phase has a lower density than the low temperature phase (when heated, a relative contraction about 4% occurs accompanying the phase transition). To exploit this aspect of zirconia, Yttrium (Y) is doped at high temperatures to act as as a meta-stabilizer for the monoclinic phase at lower temperatures. Afterwards, these meta-stable zirconia particles are mixed into the ceramic where a crack formation acts as a trigger for the suspended phase transition thus causing the zirconia particles to expand. While they expand, since they condense their vicinity, the crack's progress is stopped, followed by the closing of the shear by bringing the two sides together by further pushing towards each other. Via informatics (coordination numbers of the sites in zirconia, materials that share similar transformation procedures as zirconia, perrovskites that can be related), a list of candidate materials was prepared in the hope for being alternative to zirconia and after they were subjected to various pre-filtering processes, ab-initio calculations were performed to derive equations of state in order to find possible critical pressure values. Promising candidates were further investigated for their behaviour at high temperatures with the help of the phonon theory. Eventhough two alternatives were found, due to the fact them being more expensive than zirconia, they were swept under the rug (in the meantime, there is yet another candidate, a perrovskite whom I don't want to refer by its name, waiting for its turn to be analyzed 8)
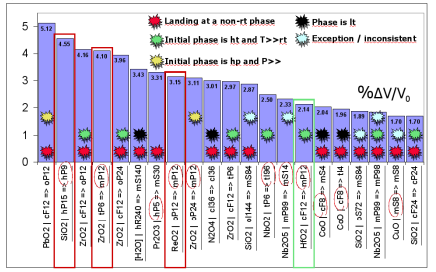
Binary search results for transformation toughening materials
Another example was the discovery of previously unknown solid state phases of gold-silicon and gold-germanium systems. These two systems possess a situation known as "eutecticity" where they form a liquid phase that has lower melting point than its constituent elements' pure states. Proposing "if we don't have a solid phase, then we'll set out from the liquidus state!", via ab-initio molecular dynamics method, we calculated the average coordination number distribution and checked for structures similar to this distribution in the database (we being, by the way, the "Dutch-French-Swiss Consortium" consisting of Dr. Marcel Sluiter, myself, Dr. Pierre Villars, Dr. Alain Pasturel and Dr. Noel Jakse). By replacing the atoms of the obtained structures with gold and silicon/germanium atoms, we checked the stabilities of these candidate structures via ab-initio calculations, succeeding in finding stable structures for both of the systems! If you're holding a thought such as "with silicon and germanium being almost the same kind of elements, it's not very surprising finding a stable structure for one following the discovery of the other...", let me express my sincere confess that it was also the thing we had in mind at first but after the results of the calculations we were surprised to see that it just wasn't the case (with my deepest respect to the platypus)!
These two systems possess a situation known as "eutecticity" where they form a liquid phase that has lower melting point than its constituent elements' pure states. Proposing "if we don't have a solid phase, then we'll set out from the liquidus state!", via ab-initio molecular dynamics method, we calculated the average coordination number distribution and checked for structures similar to this distribution in the database (we being, by the way, the "Dutch-French-Swiss Consortium" consisting of Dr. Marcel Sluiter, myself, Dr. Pierre Villars, Dr. Alain Pasturel and Dr. Noel Jakse). By replacing the atoms of the obtained structures with gold and silicon/germanium atoms, we checked the stabilities of these candidate structures via ab-initio calculations, succeeding in finding stable structures for both of the systems! If you're holding a thought such as "with silicon and germanium being almost the same kind of elements, it's not very surprising finding a stable structure for one following the discovery of the other...", let me express my sincere confess that it was also the thing we had in mind at first but after the results of the calculations we were surprised to see that it just wasn't the case (with my deepest respect to the platypus)!
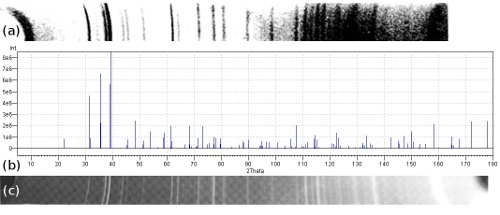
Comparison of the calculated diffraction pattern with the experiments
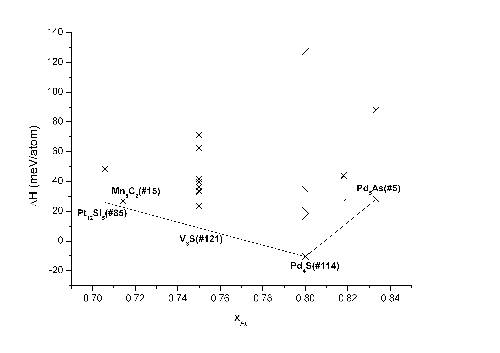
Formation enthalpies of the candidate structures with respect to Au composition in Au-Si system.
Nanostructures
Following Iijima's discovery in 1991, the interest in the nanostructures grew to extensive dimensions. Nanostructures are thought to be future's building blocks (for years and years alas it never managed to reach expected applicational level). The manufacturing of the nanotubes which have impressive properties in regards to both "mechanical" and electronic aspects is still a bit problematic and thus pretty expensive. Given the situation, we set out to conduct simulations of them (we: Dr. Sakir Erkoc, myself, Baris Malcioglu, Efe Yazgan forming the then
METU Theoretical Nanoscience group). We first started by investigating carbon nanotubes of various chiralities: we stretched, bent, heated them up, compressed, tested for their limits of endurance, merged them into each other by pushing and pushing forward...
After the nanotubes, we thought, "given that fullerenes (C60, buckyball, soccer ball) exist, why don't we play the game with the same ruler (hybrid bonds, distances, allowed planar geometries, etc.)" and thus we derived algorithms to produce nanotori, nanogears, nanojunctions (images of various examples can be viewed from my former group's gallery); testing these structures to observe their stabilities, calculating charge densities, interacting them with each other.

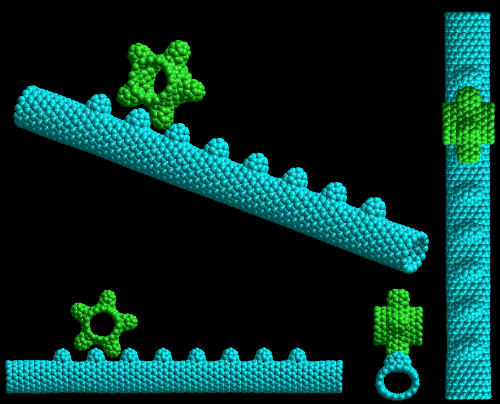
Examples for nanogears & junctions we devised, simulated and did everything that one can think of! 8)
Quantum Field Theory and Mathematical Physics
My first temptation, the first love that was first neglected, then forgotten... Back in those times (when I was an undergrad student), the rise of the nanostructures was the harbinger of the coming age of nano-interactions, thus I was studying on the "vacuum energy" and Casimir-Polder effect with my dear advisor Dr. Nese Ozdemir, in a way paving the way for future research but as it turned out my commitment in this field wasn't in the dealt of the cards. As I came to METU, one of the two professors on the subject (Dr. Tekin Dereli) was abroad, while the other (Dr. Selcuk Bayin) wasn't accepting thesis students anymore. But the ones in a similar situation, worry no more, lo! Because now METU has it's own Dr. Bayram Tekin! 8)
P.S. : The figures are taken from the publications resulted from the research topics presented above. You can find the list of the publications in my curriculum vitae, as well as in the "Docs" page.

 "Self-healing" is an example to these sought properties: ZrO2 (Zirconia) is a material that is monoclinic at room temperature and tetragonal at highter temperatures (it transforms into cubic at even higher temperatures but this last phase isn't that relevant to our purposes). Contrary to the standard behaviour, similar to the water between 0-4 degrees C, its high temperature phase has a lower density than the low temperature phase (when heated, a relative contraction about 4% occurs accompanying the phase transition). To exploit this aspect of zirconia, Yttrium (Y) is doped at high temperatures to act as as a meta-stabilizer for the monoclinic phase at lower temperatures. Afterwards, these meta-stable zirconia particles are mixed into the ceramic where a crack formation acts as a trigger for the suspended phase transition thus causing the zirconia particles to expand. While they expand, since they condense their vicinity, the crack's progress is stopped, followed by the closing of the shear by bringing the two sides together by further pushing towards each other. Via informatics (coordination numbers of the sites in zirconia, materials that share similar transformation procedures as zirconia, perrovskites that can be related), a list of candidate materials was prepared in the hope for being alternative to zirconia and after they were subjected to various pre-filtering processes, ab-initio calculations were performed to derive equations of state in order to find possible critical pressure values. Promising candidates were further investigated for their behaviour at high temperatures with the help of the phonon theory. Eventhough two alternatives were found, due to the fact them being more expensive than zirconia, they were swept under the rug (in the meantime, there is yet another candidate, a perrovskite whom I don't want to refer by its name, waiting for its turn to be analyzed 8)
"Self-healing" is an example to these sought properties: ZrO2 (Zirconia) is a material that is monoclinic at room temperature and tetragonal at highter temperatures (it transforms into cubic at even higher temperatures but this last phase isn't that relevant to our purposes). Contrary to the standard behaviour, similar to the water between 0-4 degrees C, its high temperature phase has a lower density than the low temperature phase (when heated, a relative contraction about 4% occurs accompanying the phase transition). To exploit this aspect of zirconia, Yttrium (Y) is doped at high temperatures to act as as a meta-stabilizer for the monoclinic phase at lower temperatures. Afterwards, these meta-stable zirconia particles are mixed into the ceramic where a crack formation acts as a trigger for the suspended phase transition thus causing the zirconia particles to expand. While they expand, since they condense their vicinity, the crack's progress is stopped, followed by the closing of the shear by bringing the two sides together by further pushing towards each other. Via informatics (coordination numbers of the sites in zirconia, materials that share similar transformation procedures as zirconia, perrovskites that can be related), a list of candidate materials was prepared in the hope for being alternative to zirconia and after they were subjected to various pre-filtering processes, ab-initio calculations were performed to derive equations of state in order to find possible critical pressure values. Promising candidates were further investigated for their behaviour at high temperatures with the help of the phonon theory. Eventhough two alternatives were found, due to the fact them being more expensive than zirconia, they were swept under the rug (in the meantime, there is yet another candidate, a perrovskite whom I don't want to refer by its name, waiting for its turn to be analyzed 8)
 These two systems possess a situation known as "eutecticity" where they form a liquid phase that has lower melting point than its constituent elements' pure states. Proposing "if we don't have a solid phase, then we'll set out from the liquidus state!", via ab-initio molecular dynamics method, we calculated the average coordination number distribution and checked for structures similar to this distribution in the database (we being, by the way, the "Dutch-French-Swiss Consortium" consisting of Dr. Marcel Sluiter, myself, Dr. Pierre Villars, Dr. Alain Pasturel and Dr. Noel Jakse). By replacing the atoms of the obtained structures with gold and silicon/germanium atoms, we checked the stabilities of these candidate structures via ab-initio calculations, succeeding in finding stable structures for both of the systems! If you're holding a thought such as "with silicon and germanium being almost the same kind of elements, it's not very surprising finding a stable structure for one following the discovery of the other...", let me express my sincere confess that it was also the thing we had in mind at first but after the results of the calculations we were surprised to see that it just wasn't the case (with my deepest respect to the platypus)!
These two systems possess a situation known as "eutecticity" where they form a liquid phase that has lower melting point than its constituent elements' pure states. Proposing "if we don't have a solid phase, then we'll set out from the liquidus state!", via ab-initio molecular dynamics method, we calculated the average coordination number distribution and checked for structures similar to this distribution in the database (we being, by the way, the "Dutch-French-Swiss Consortium" consisting of Dr. Marcel Sluiter, myself, Dr. Pierre Villars, Dr. Alain Pasturel and Dr. Noel Jakse). By replacing the atoms of the obtained structures with gold and silicon/germanium atoms, we checked the stabilities of these candidate structures via ab-initio calculations, succeeding in finding stable structures for both of the systems! If you're holding a thought such as "with silicon and germanium being almost the same kind of elements, it's not very surprising finding a stable structure for one following the discovery of the other...", let me express my sincere confess that it was also the thing we had in mind at first but after the results of the calculations we were surprised to see that it just wasn't the case (with my deepest respect to the platypus)!

 Following Iijima's discovery in 1991, the interest in the nanostructures grew to extensive dimensions. Nanostructures are thought to be future's building blocks (for years and years alas it never managed to reach expected applicational level). The manufacturing of the nanotubes which have impressive properties in regards to both "mechanical" and electronic aspects is still a bit problematic and thus pretty expensive. Given the situation, we set out to conduct simulations of them (we: Dr. Sakir Erkoc, myself, Baris Malcioglu, Efe Yazgan forming the then
Following Iijima's discovery in 1991, the interest in the nanostructures grew to extensive dimensions. Nanostructures are thought to be future's building blocks (for years and years alas it never managed to reach expected applicational level). The manufacturing of the nanotubes which have impressive properties in regards to both "mechanical" and electronic aspects is still a bit problematic and thus pretty expensive. Given the situation, we set out to conduct simulations of them (we: Dr. Sakir Erkoc, myself, Baris Malcioglu, Efe Yazgan forming the then 



